Trigonométrie_1
TRIGONOMETRIE
A0. Les bases.
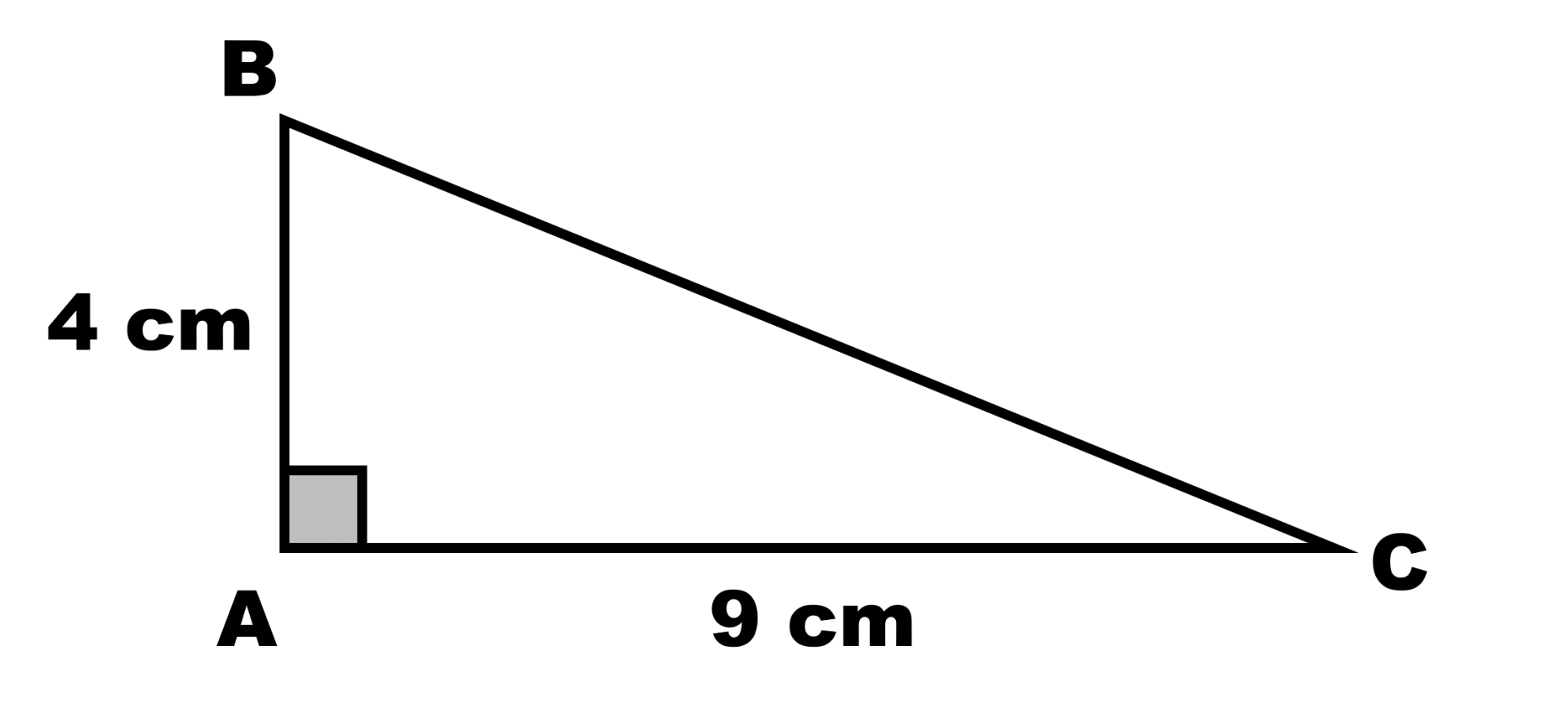
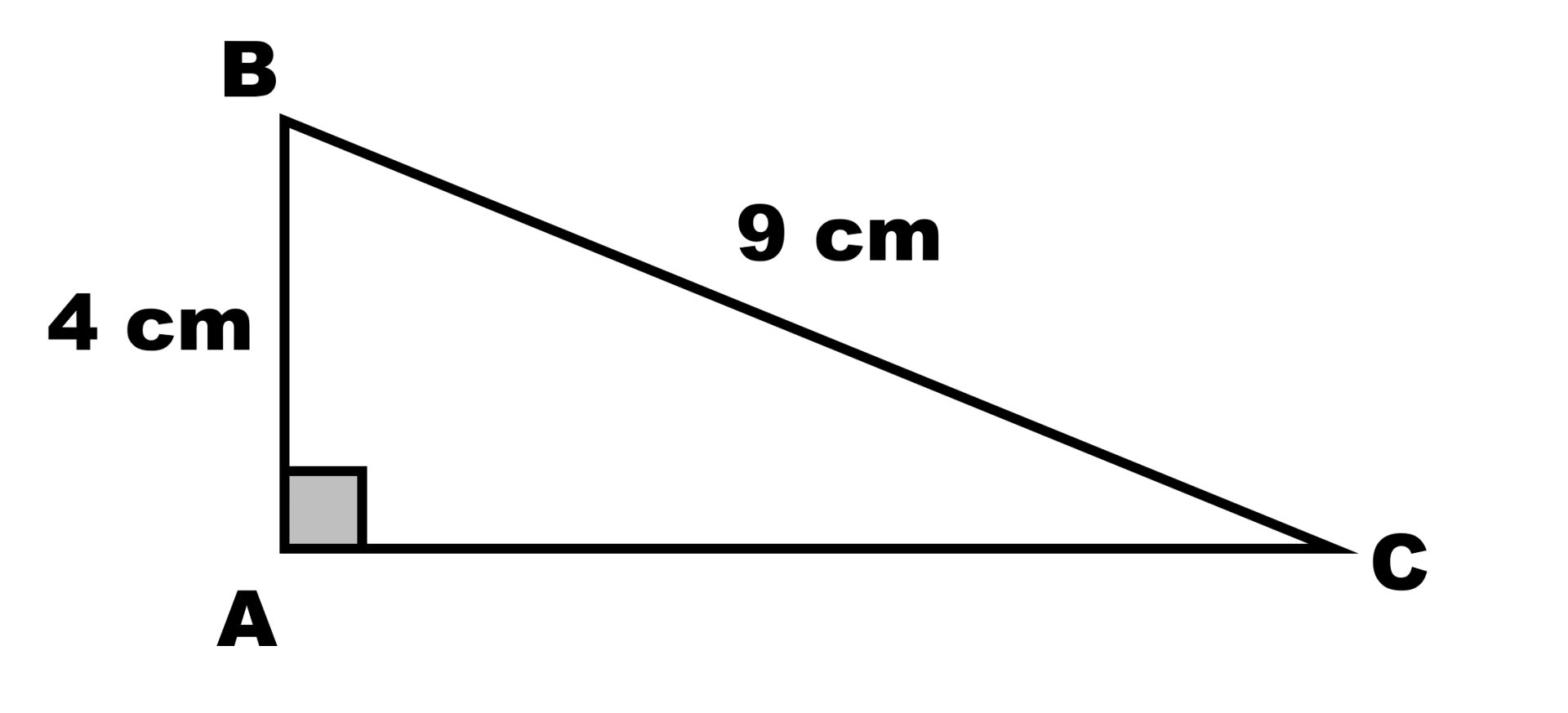
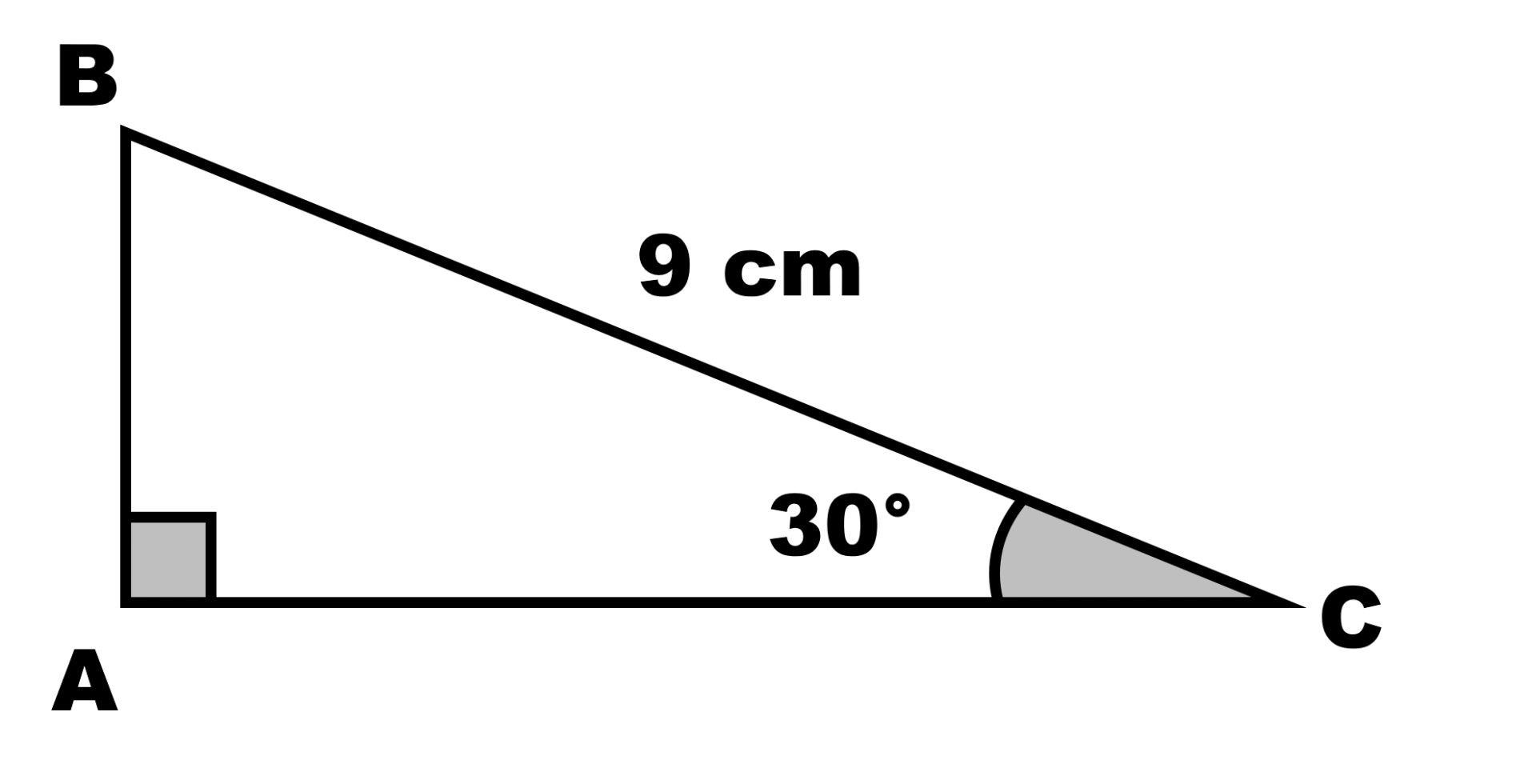
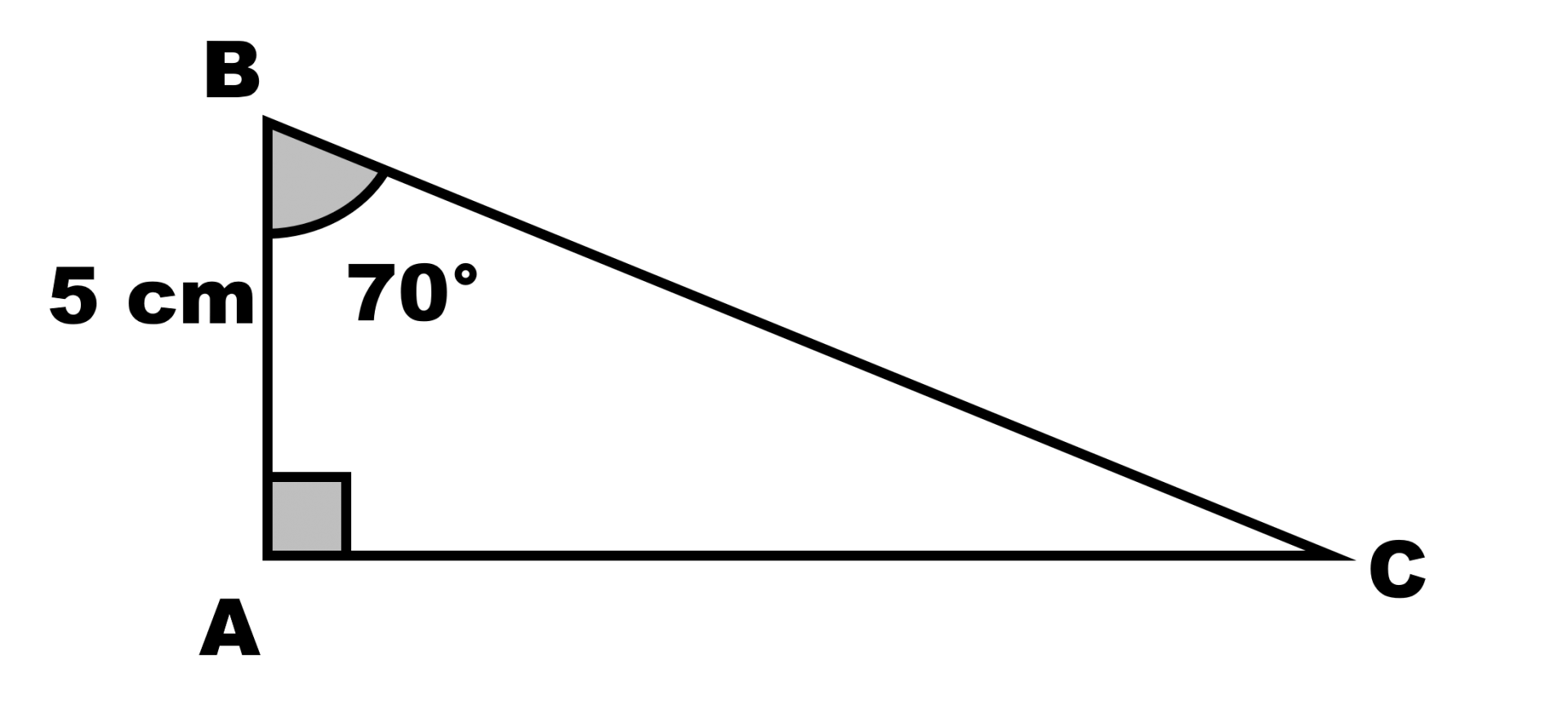
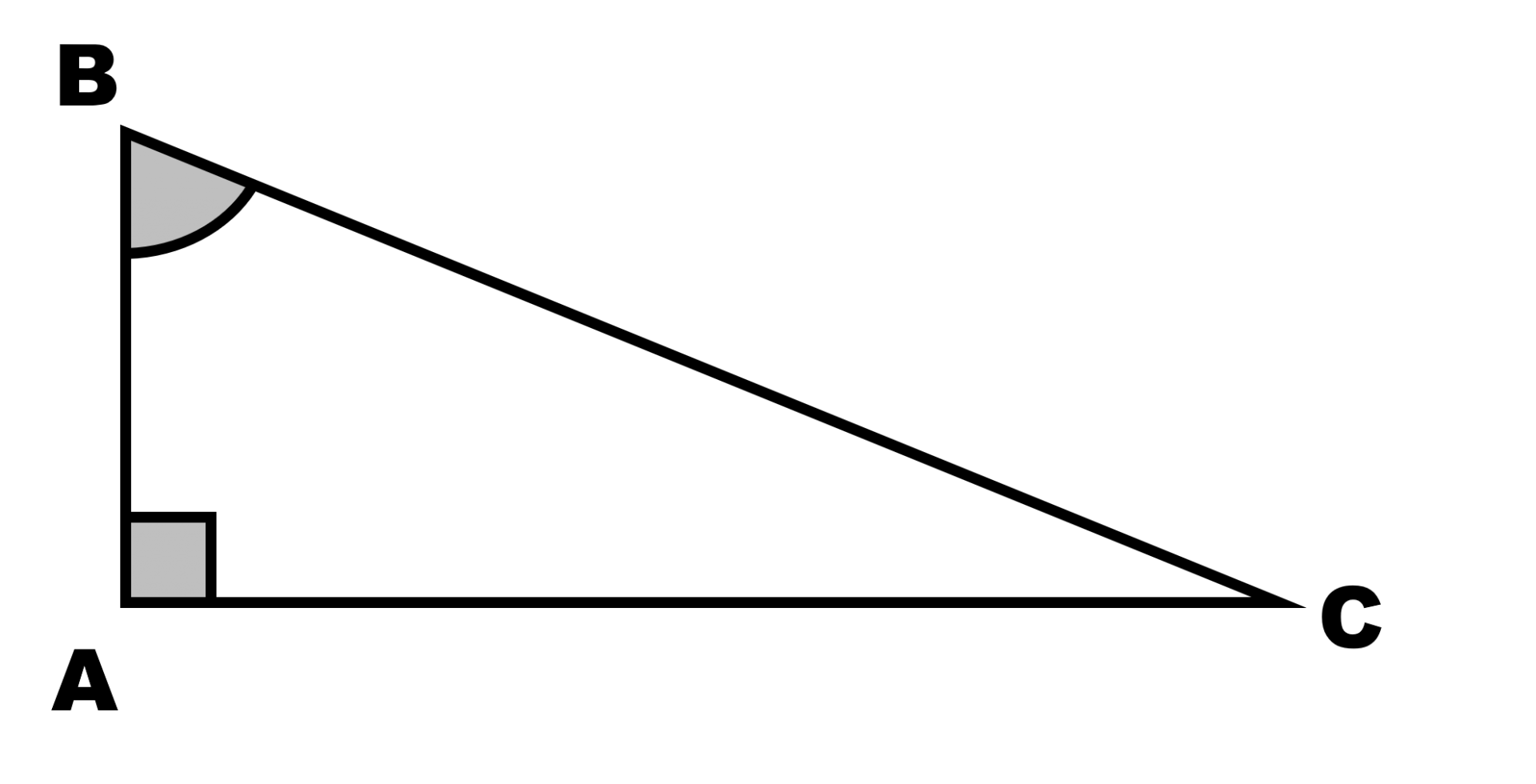
Dans chaque triangle rectangle ci-dessous, déterminer la longueur des côtés et les valeurs des angles qui n’apparaissent pas.
|
a.
........................................................................................................................................ ........................................................................................................................................ ........................................................................................................................................ ........................................................................................................................................ |
b.
........................................................................................................................................ ........................................................................................................................................ ........................................................................................................................................ ........................................................................................................................................ |
|
c.
........................................................................................................................................ ........................................................................................................................................ ........................................................................................................................................ ........................................................................................................................................ |
d.
........................................................................................................................................ ........................................................................................................................................ ........................................................................................................................................ ........................................................................................................................................ |
RAPPELS :
|
|
Théorème de Pythagore : ................................................................. $cos \widehat B =$.................... ; $cos \widehat C =$.................... $sin \widehat B =$.................... ; $sin \widehat C =$.................... $tan \widehat B =$.................... ; $tan \widehat C =$.................... |
A1. Le radian.
A11. Longueur d'un arc de cercle.
A11a. Expérience 1.
$\bullet$ Déplacer le curseur R.
https://www.geogebra.org/m/twfcsgmj
$\bullet$ Compléter le tableau ci-dessous.
|
Arc de cercle. |
$1$ |
$2$ |
$3$ |
$4$ |
$5$ |
$6$ |
|
Longueur L |
||||||
|
Rayon R |
||||||
|
$\dfrac {L}{R}$ |
$\bullet$ Quelle grandeur n’a pas varié pour les six arcs-de-cercle ? .....................................
$\bullet$ Conclusion 1 : La longueur $L$ de l'arc de cercle est ......................... au ....................
$L \ = \ ....... \times .......$
A11b. Expérience 2.
$\bullet$ Déplacer le curseur $\alpha$.
https://www.geogebra.org/m/haqvqv8n
$\bullet$ Compléter le tableau ci-dessous.
|
Arc de cercle. |
$1$ |
$2$ |
$3$ |
$4$ |
$5$ |
$6$ |
|
Longueur L |
||||||
|
Angle $\alpha$ |
||||||
|
$\dfrac {L}{\alpha}$ |
$\bullet$ Quelle grandeur n’a pas varié pour les six arcs-de-cercle ? .....................................
$\bullet$ Conclusion 2 : La longueur $L$ de l'arc de cercle est ......................... à ....................
$L \ = \ ....... \times .......$
A11b. Conclusion :
$\bullet$ La longueur de l'arc de cercle est .................... au .................. et à ...................
$\bullet$ Cette longueur ne dépend que de ces paramètres.
Donc :
|
$L \ = \ .......................$ |
A12. Définition.
$\bullet$ Sur le cercle de rayon $R \ = \ 1$, pour quelle valeur de l'angle $\alpha$, la longueur $L$ est-elle égale à $1$ ? ..............................................................
$\bullet$ Quelle est la longueur du demi-cercle ? ..............................................................
$\bullet$ Quel est la valeur de l’angle correspondant ? ..............................................................
$\bullet$ Quel est ce nombre ? ..............................................................
|
Le radian correspond à l’angle qui intercepte une longueur de 1 sur un cercle de rayon 1. L'angle plat (180°) correspond à ................. radians. |
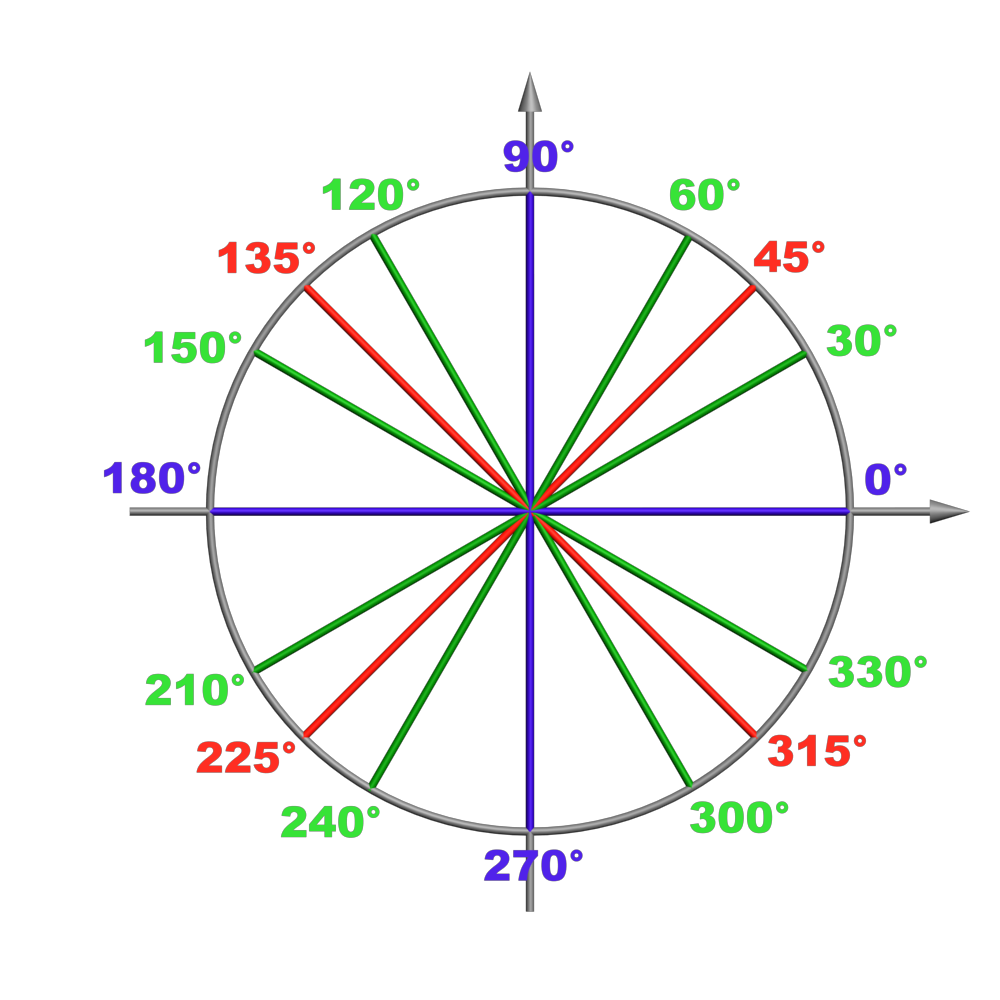
A13. Position d'angle courants.
Pour chacun des angles exprimés en degrés, donner la valeur de l’angle en radians sur le cercle trigonométrique.
A2. Les fonctions trigonométriques.
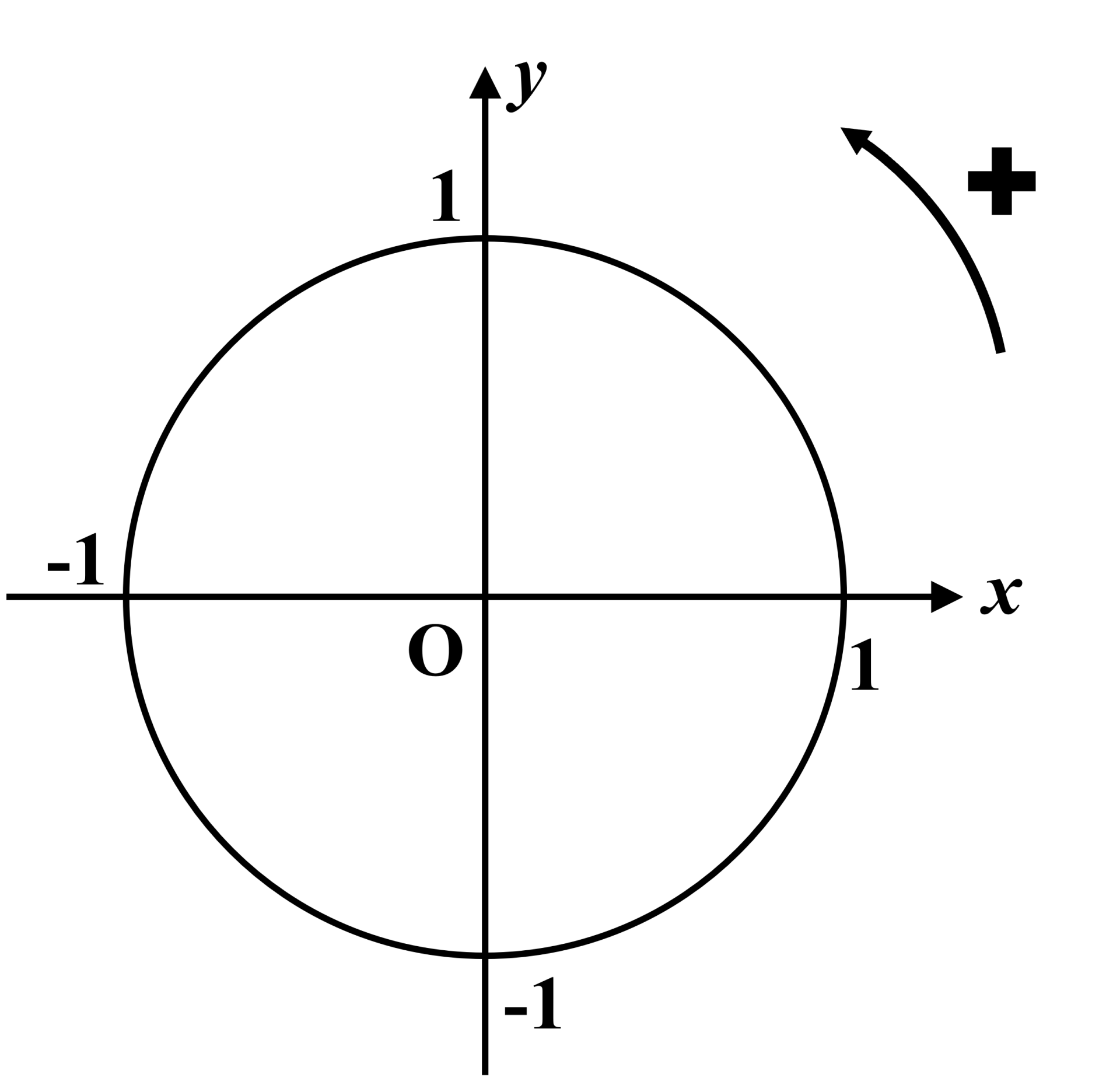
A21. Le cercle trigonométrique.
|
Le cercle trigonométrique a pour centre $O \left ( 0 \ ; \ 0 \right )$ et pour rayon $R \ = \ 1$. Le plan est orienté : le sens de rotation est le sens antihoraire.  |
 |
A22. Définitions.
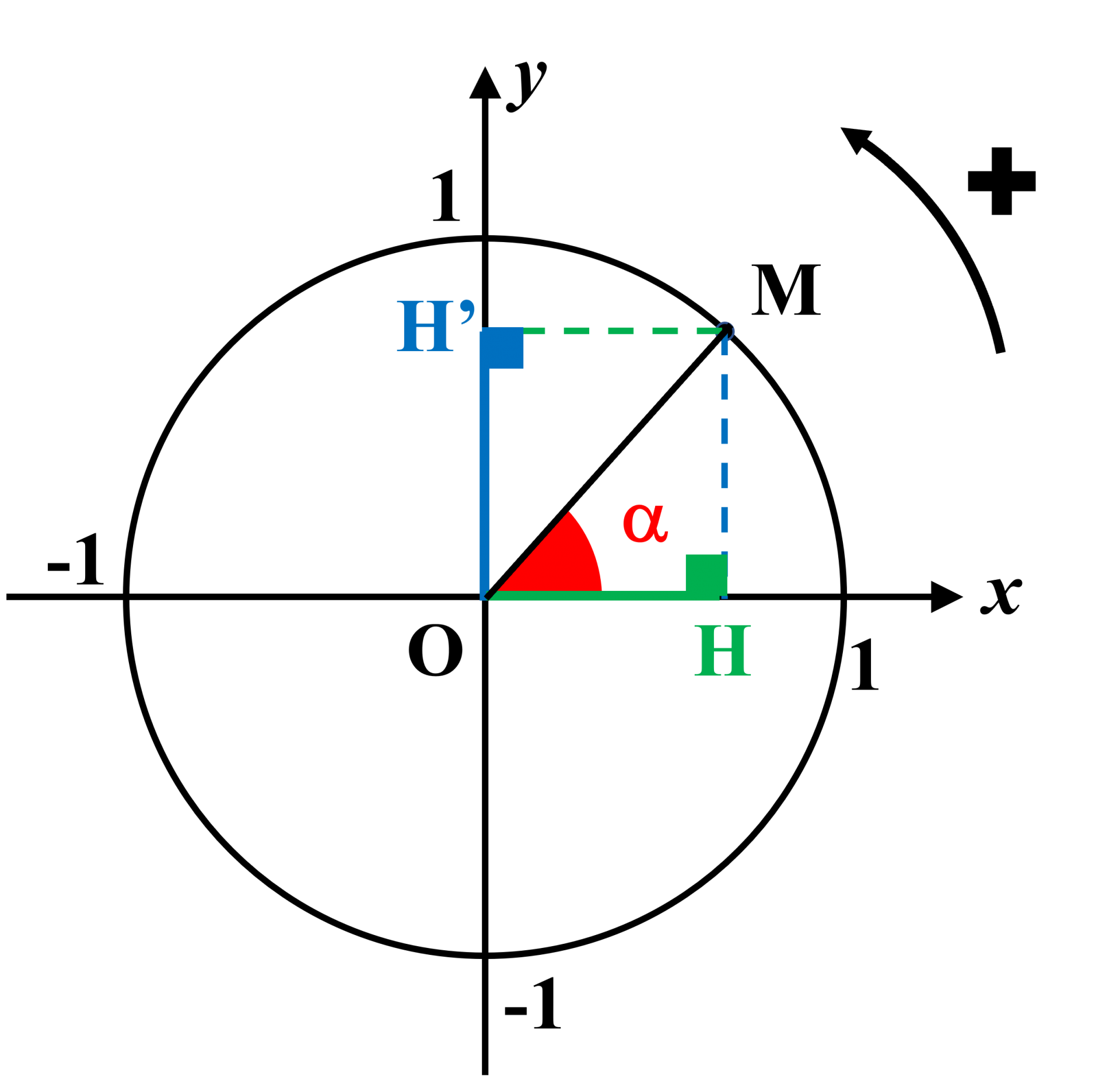 |
$\bullet$ On considère le point $M$ sur le cercle trigonométrique. $\bullet$ On note $\alpha$, l'angle $\widehat {HOM}$. $\bullet$ $H$ est le projeté orthogonal de $M$ sur l'axe des abscisses. $\bullet$ $H'$ est le projeté orthogonal de $M$ sur l'axe des ordonnées. |
1. En se plaçant dans le triangle rectangle $OHM$, déterminer l'abscisse du point $M$.
............................................................
2. En se plaçant dans le triangle rectangle $OHM$, déterminer l'ordonnée du point $M$.
............................................................
3. En utilisant le théorème de Pythagore, déterminer une relation entre ces deux grandeurs.
............................................................
4. Dans quel intervalle se trouvent ces deux grandeurs ?
............................................................
A23. Représentations graphiques.
A23a. Le sinus.
$\bullet$ En utilisant Geogebra, représenter la fonction $x \mapsto sin x$ pour $x \in \left [ -2 \pi \ ; \ 2 \pi \right ]$.
$\bullet$ Déterminer la période de la fonction $x \mapsto sin x$. ...........................................
$\bullet$ Déterminer la parité de la fonction $x \mapsto sin x$. ...........................................
A23. Représentations graphiques.
A23a. Le cosinus.
$\bullet$ En utilisant Geogebra, représenter la fonction $x \mapsto cos x$ pour $x \in \left [ -2 \pi \ ; \ 2 \pi \right ]$.

$\bullet$ Déterminer la période de la fonction $x \mapsto cos x$. ...........................................
$\bullet$ Déterminer la parité de la fonction $x \mapsto cos x$. ...........................................
A3. Les relations entre le cosinus et le sinus.
A31. Valeurs particulières.
|
Angle en degrés |
$0$ |
$30$ |
$45$ |
$60$ |
$90$ |
$180$ |
|
Angle en radians |
$0$ |
$\dfrac{\pi}{6}$ |
$\dfrac{\pi}{4}$ |
$\dfrac{\pi}{3}$ |
$\dfrac{\pi}{2}$ |
$\pi$ |
|
$sin$ |
$0$ |
$\dfrac{1}{2}$ |
$\dfrac{\sqrt 2}{2}$ |
$\dfrac{\sqrt 3}{2}$ |
$1$ |
$0$ |
|
$cos$ |
$1$ |
$\dfrac{\sqrt 3}{2}$ |
$\dfrac{\sqrt 2}{2}$ |
$\dfrac{1}{2}$ |
$0$ |
$-1$ |
A32. Relations.
A32a. Angle opposé.
 |
$ \bullet$ Placer les angles $\alpha$ et $ - \ \alpha$ sur le cercle trigonométrique. $ \bullet$ En déduire la relation entre $cos \left ( \alpha \right )$ et $cos \left ( - \ \alpha \right )$ . $ \bullet$ En déduire la relation entre $sin \left ( \alpha \right )$ et $sin \left ( - \ \alpha \right )$ . |
En utilisant Geogebra :
$\bullet$ Vérifier la première relation en traçant les fonctions $x \mapsto cos \left ( \alpha \right )$ et $x \mapsto cos \left ( - \ \alpha \right )$
$\bullet$ Vérifier la première relation en traçant les fonctions $x \mapsto sin \left ( \alpha \right )$ et $x \mapsto sin \left ( - \ \alpha \right )$
A32b. Angle supplémentaitre.
$\bullet \ \alpha \ \ et \ \ \pi - \alpha$
 |
$ \bullet$ Placer les angles $\alpha$ et $ \pi - \alpha$ sur le cercle trigonométrique. $ \bullet$ En déduire la relation entre $cos \left ( \alpha \right )$ et $cos \left ( \pi - \alpha \right )$ . $ \bullet$ En déduire la relation entre $sin \left ( \alpha \right )$ et $sin \left ( \pi - \alpha \right )$ . |
En utilisant Geogebra :
$\bullet$ Vérifier la première relation en traçant les fonctions $x \mapsto cos \left ( \alpha \right )$ et $x \mapsto cos \left ( \pi - \alpha \right )$
$\bullet$ Vérifier la première relation en traçant les fonctions $x \mapsto sin \left ( \alpha \right )$ et $x \mapsto sin \left ( \pi - \alpha \right )$
$\bullet \ \alpha \ \ et \ \ \pi + \alpha$
 |
$ \bullet$ Placer les angles $\alpha$ et $ \pi + \alpha$ sur le cercle trigonométrique. $ \bullet$ En déduire la relation entre $cos \left ( \alpha \right )$ et $cos \left ( \pi + \alpha \right )$ . $ \bullet$ En déduire la relation entre $sin \left ( \alpha \right )$ et $sin \left ( \pi + \alpha \right )$ . |
En utilisant Geogebra :
$\bullet$ Vérifier la première relation en traçant les fonctions $x \mapsto cos \left ( \alpha \right )$ et $x \mapsto cos \left ( \pi + \alpha \right )$
$\bullet$ Vérifier la première relation en traçant les fonctions $x \mapsto sin \left ( \alpha \right )$ et $x \mapsto sin \left ( \pi + \alpha \right )$
A32c. Angle complémentaire.
$\bullet \ \alpha \ \ et \ \ \dfrac{\pi}{2} - \alpha$
 |
$ \bullet$ Placer les angles $\alpha$ et $ \dfrac{\pi}{2} - \alpha$ sur le cercle trigonométrique. $ \bullet$ En déduire la relation entre $cos \left ( \alpha \right )$ et $sin \left ( \dfrac{\pi}{2} - \alpha \right )$ . $ \bullet$ En déduire la relation entre $sin \left ( \alpha \right )$ et $cos \left ( \dfrac{\pi}{2} - \alpha \right )$ . |
En utilisant Geogebra :
$\bullet$ Vérifier la première relation en traçant les fonctions $x \mapsto cos \left ( \alpha \right )$ et $x \mapsto sin \left ( \dfrac{\pi}{2} - \alpha \right )$
$\bullet$ Vérifier la première relation en traçant les fonctions $x \mapsto sin \left ( \alpha \right )$ et $x \mapsto cos \left ( \dfrac{\pi}{2} - \alpha \right )$
$\bullet \ \alpha \ \ et \ \ \dfrac{\pi}{2} + \alpha$
 |
$ \bullet$ Placer les angles $\alpha$ et $ \dfrac{\pi}{2} + \alpha$ sur le cercle trigonométrique. $ \bullet$ En déduire la relation entre $cos \left ( \alpha \right )$ et $sin \left ( \dfrac{\pi}{2} + \alpha \right )$ . $ \bullet$ En déduire la relation entre $sin \left ( \alpha \right )$ et $cos \left ( \dfrac{\pi}{2} + \alpha \right )$ . |
En utilisant Geogebra :
$\bullet$ Vérifier la première relation en traçant les fonctions $x \mapsto cos \left ( \alpha \right )$ et $x \mapsto sin \left ( \dfrac{\pi}{2} + \alpha \right )$
$\bullet$ Vérifier la première relation en traçant les fonctions $x \mapsto sin \left ( \alpha \right )$ et $x \mapsto cos \left ( \dfrac{\pi}{2}+ \alpha \right )$
COURS
A1. Le cercle trigonométrique.
|
Le cercle trigonométrique a pour centre $O \left ( 0 \ ; \ 0 \right )$ et pour rayon $R = 1$. Le plan est orienté : le sens de rotation est le sens antihoraire.
|
 |
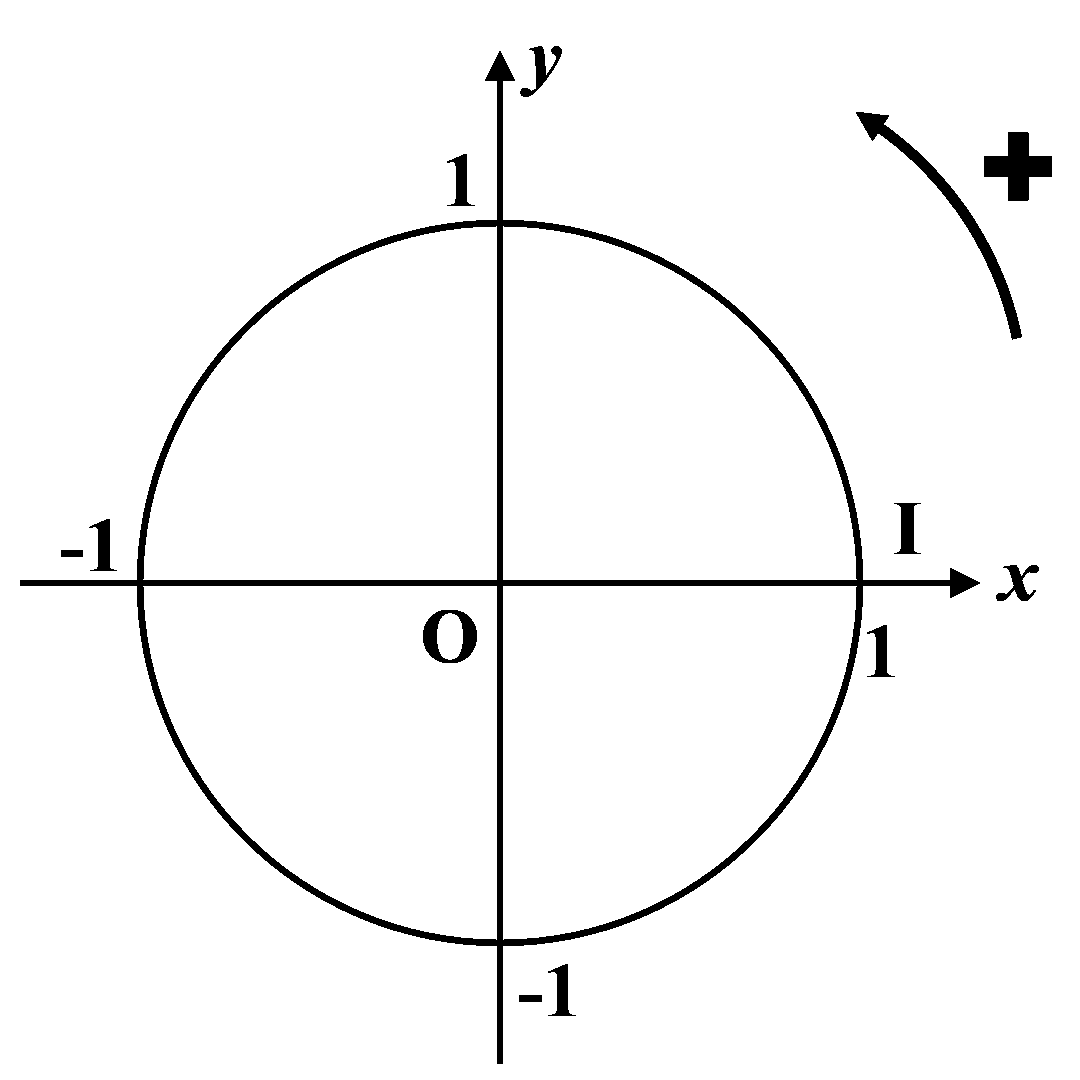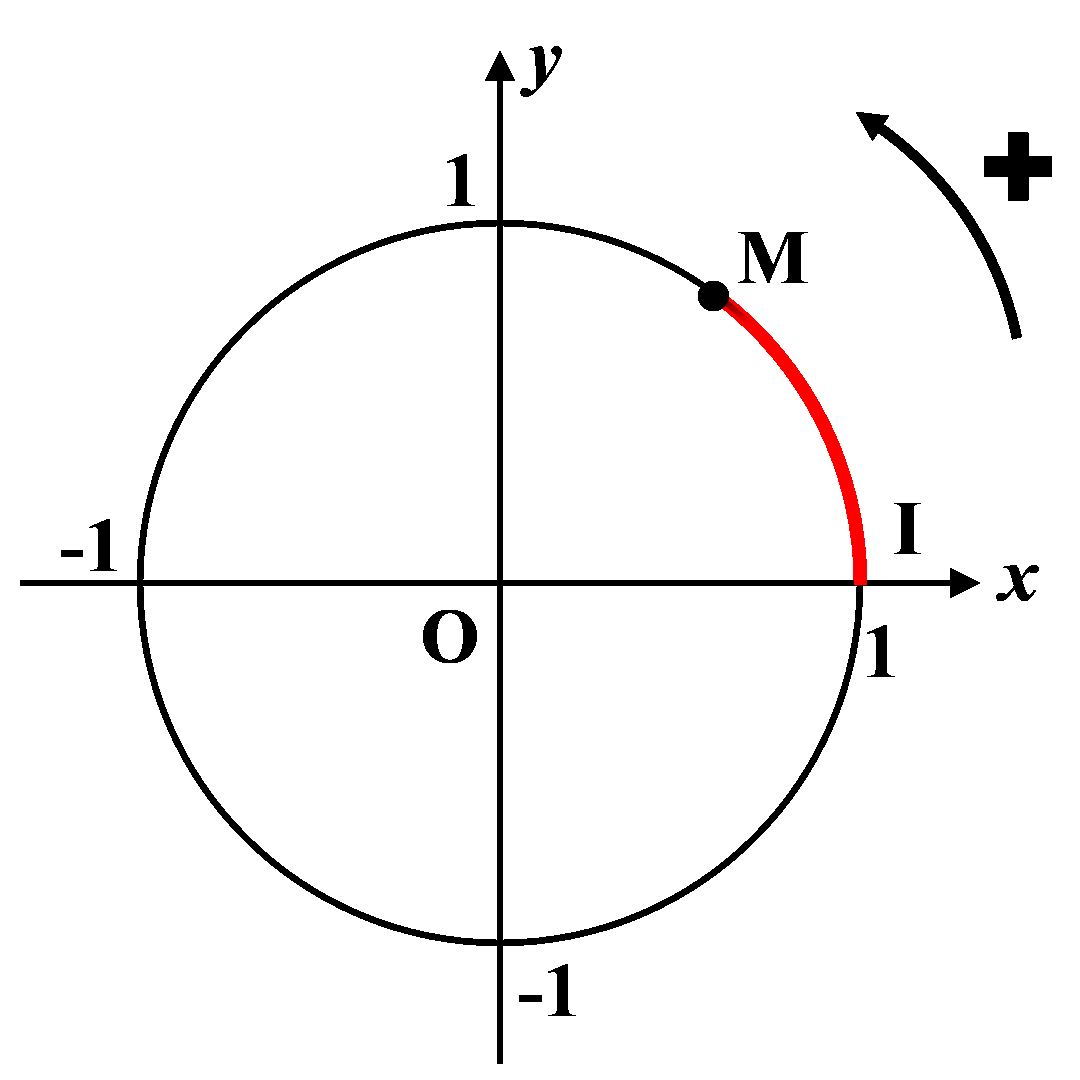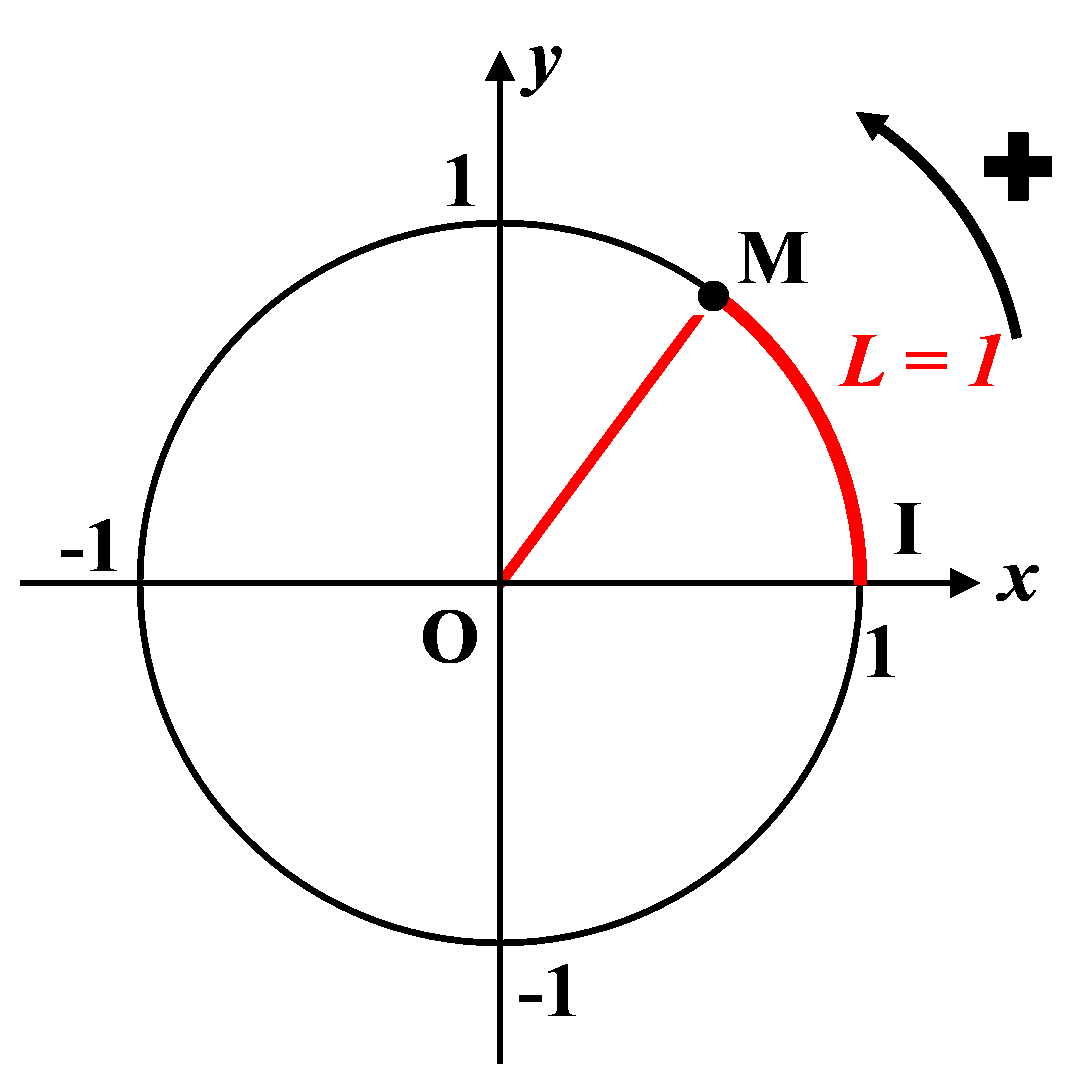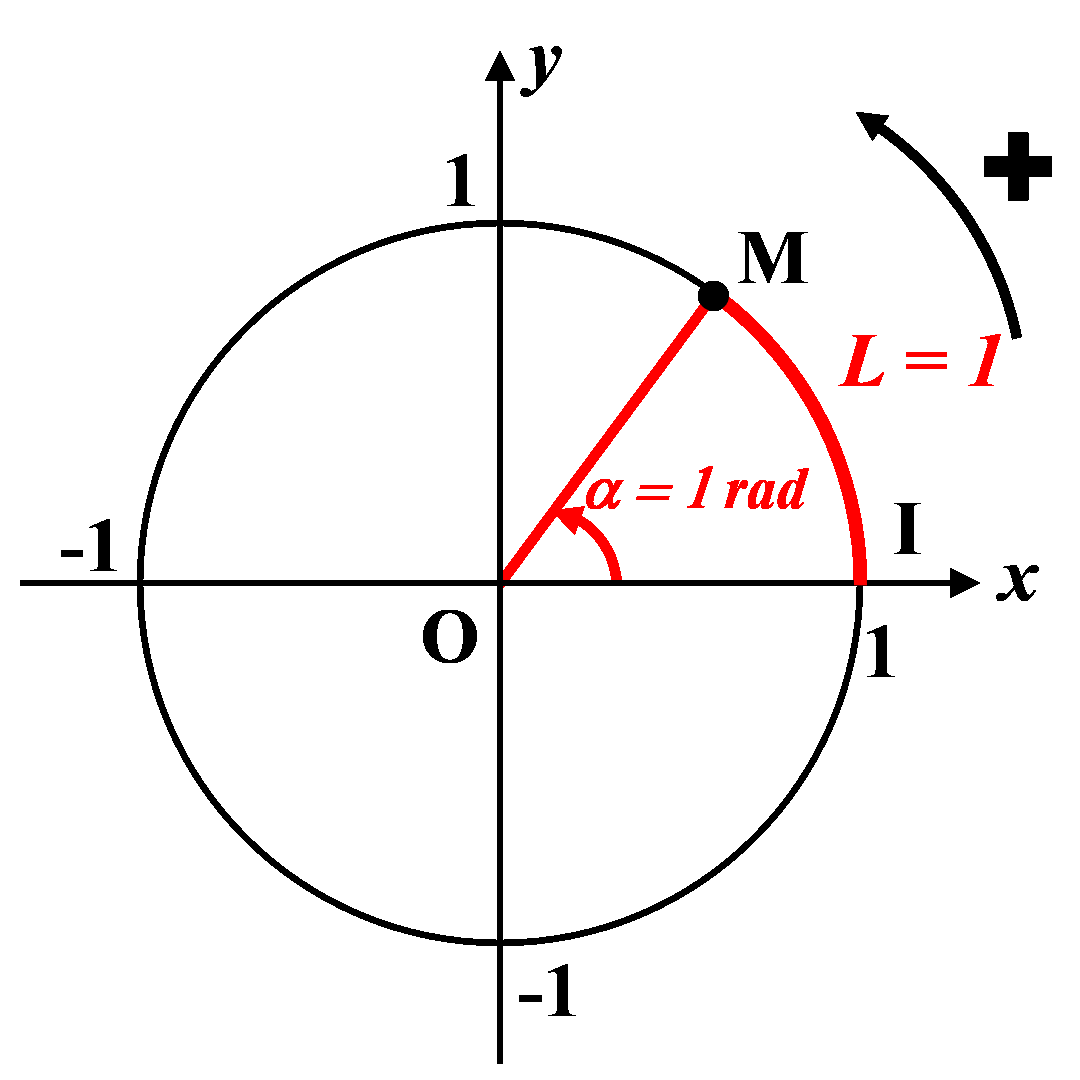
C2. Le radian.
|
Le radian correspond à l’angle qui intercepte une longueur $L = 1$ sur le cercle trigonométrique. |
 |
C3. Le sinus et le cosinus.
|
On considère un nombre $\alpha$ quelconque. Sur le cercle trigonométrique, on place le point tel que : $\left ( \overrightarrow{OI} ; \overrightarrow{OM} \right ) = \alpha$ $\bullet$ L'abscisse du point $M$ correspond au cosinus de l'angle $\alpha$
$\bullet$ L'ordonnée du point $M$ correspond au sinus de l'angle $\alpha$ |
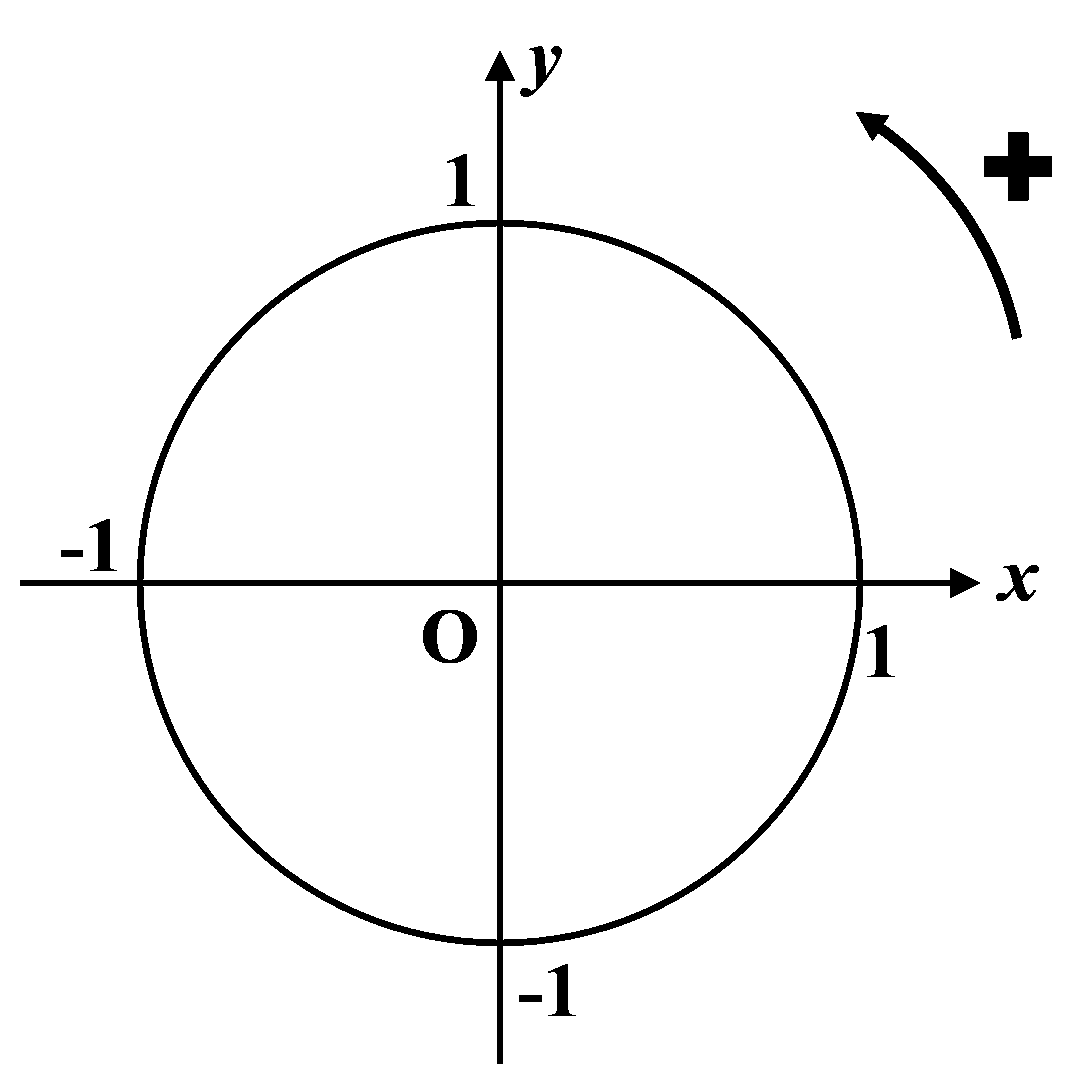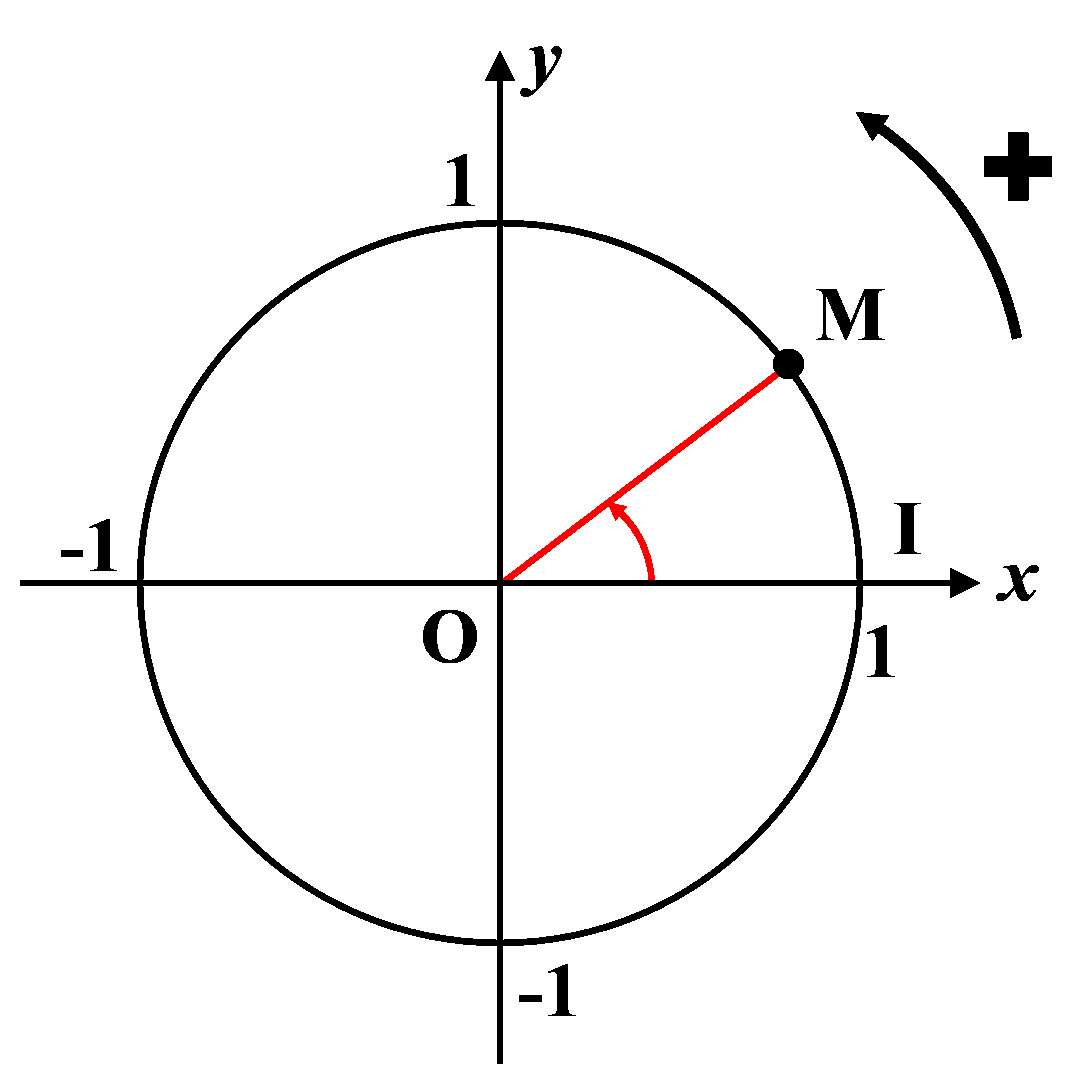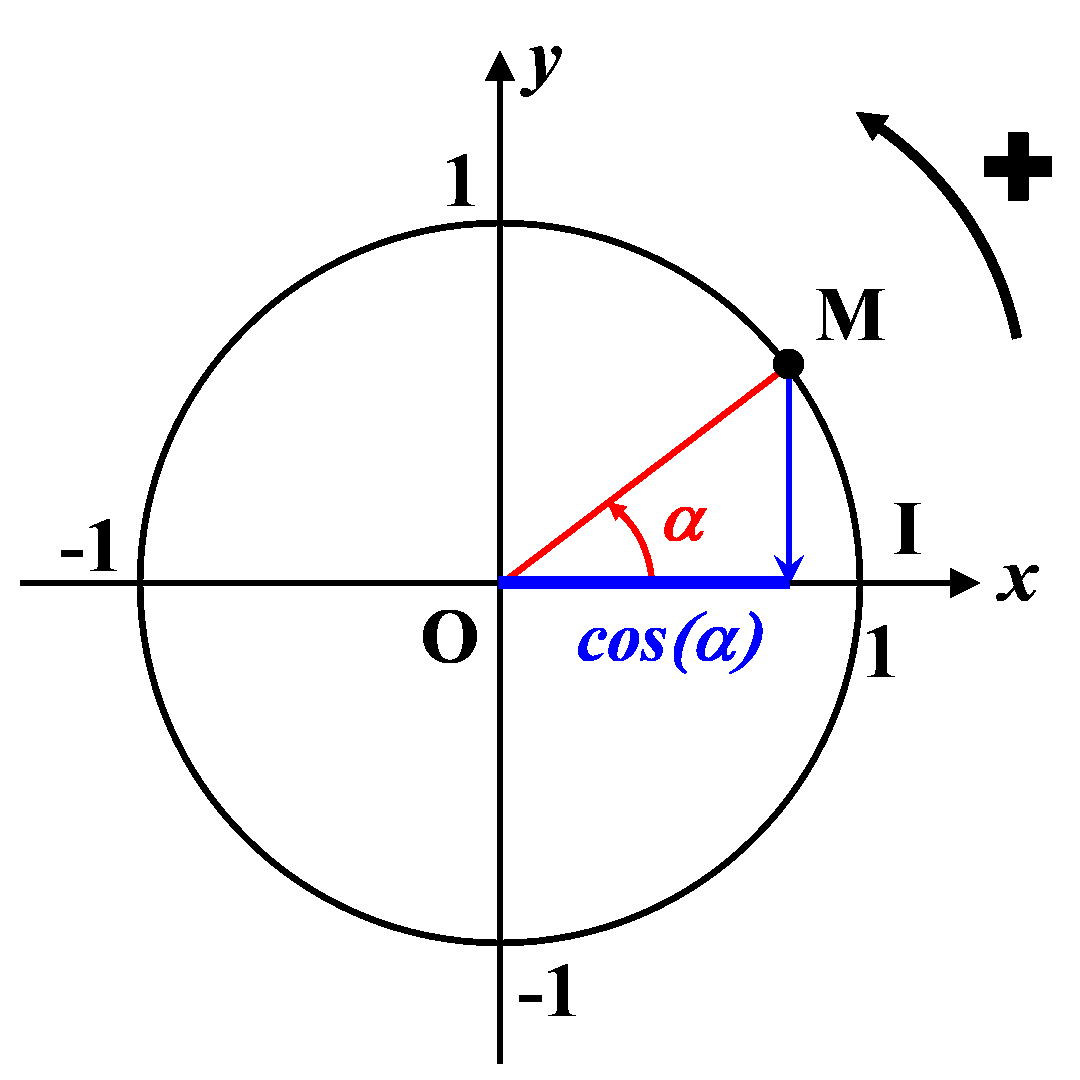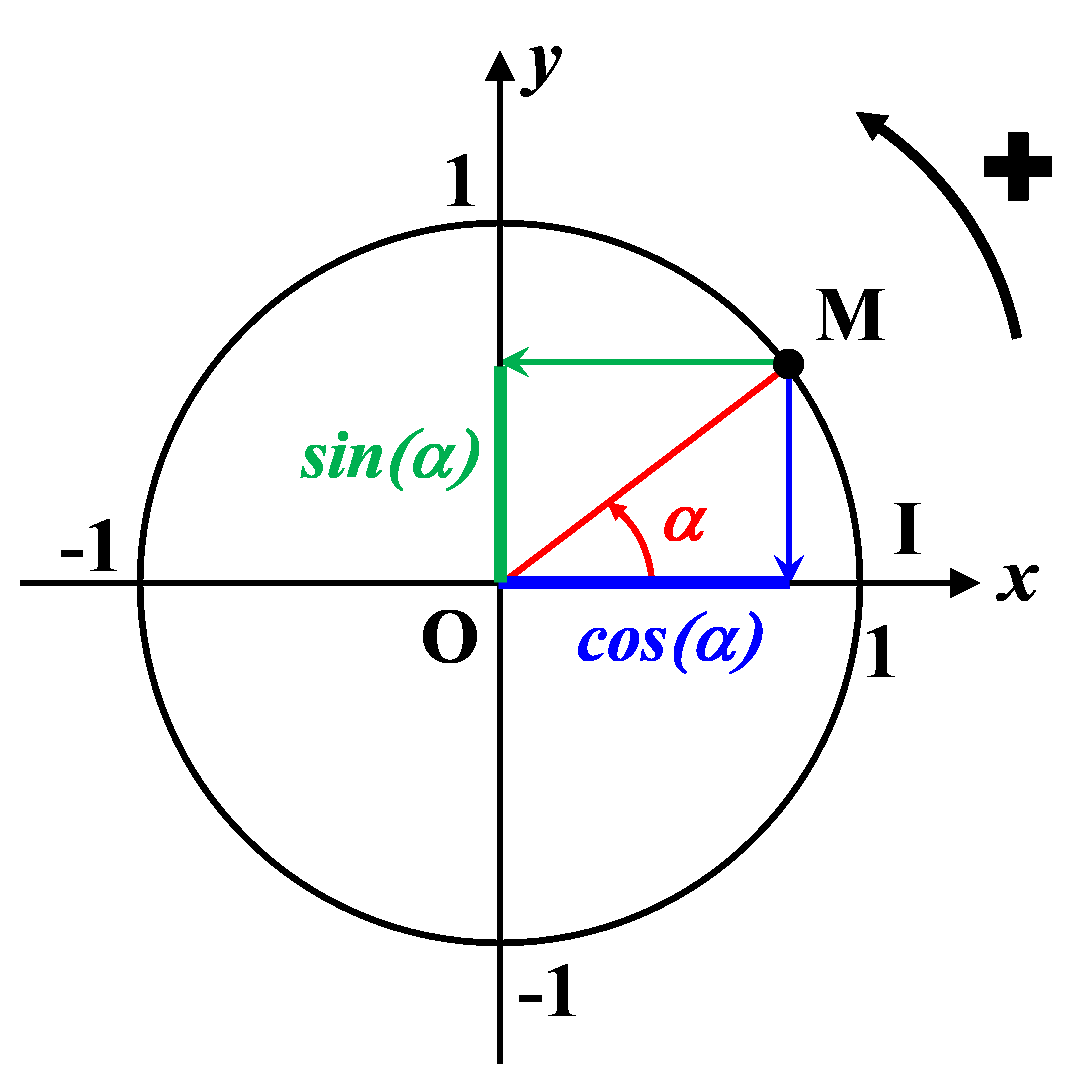 |
Remarques FONDAMENTALES :
$\bullet \ -1 \ \leq \ cos(\alpha) \ \leq \ +1$
$\bullet \ -1 \ \leq \ sin(\alpha) \ \leq \ +1$
$\bullet \ cos^2(\alpha) \ + \ sin^2(\alpha) \ = 1$
C4. Angles associés.
C41. Angles opposés.
|
$\bullet$ Les angles opposés ont le même cosinus : $cos(-\alpha) \ = \ cos(\alpha)$
$\bullet$ Les angles opposés ont des sinus opposés : $sin(-\alpha) \ = \ - \ sin(\alpha)$ |
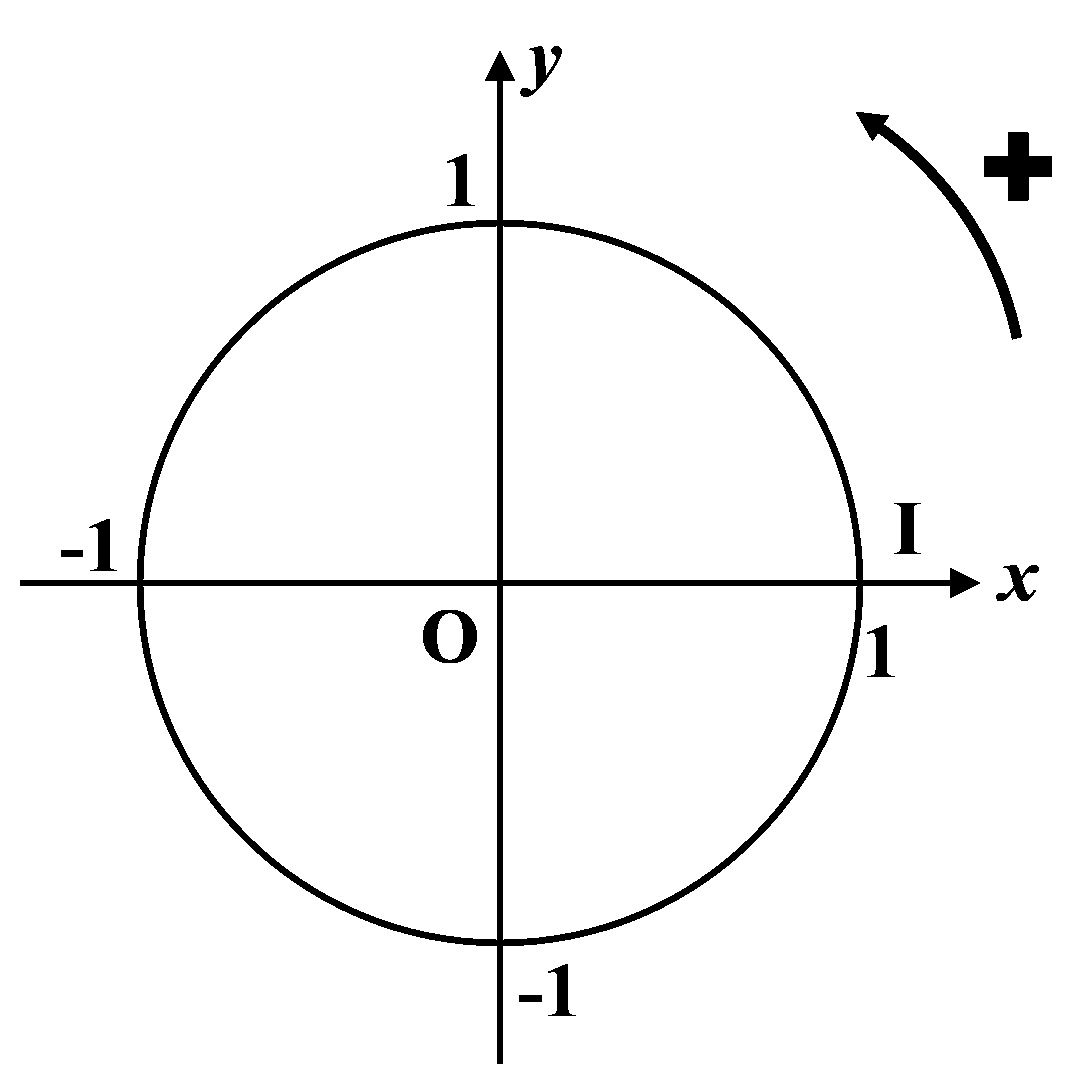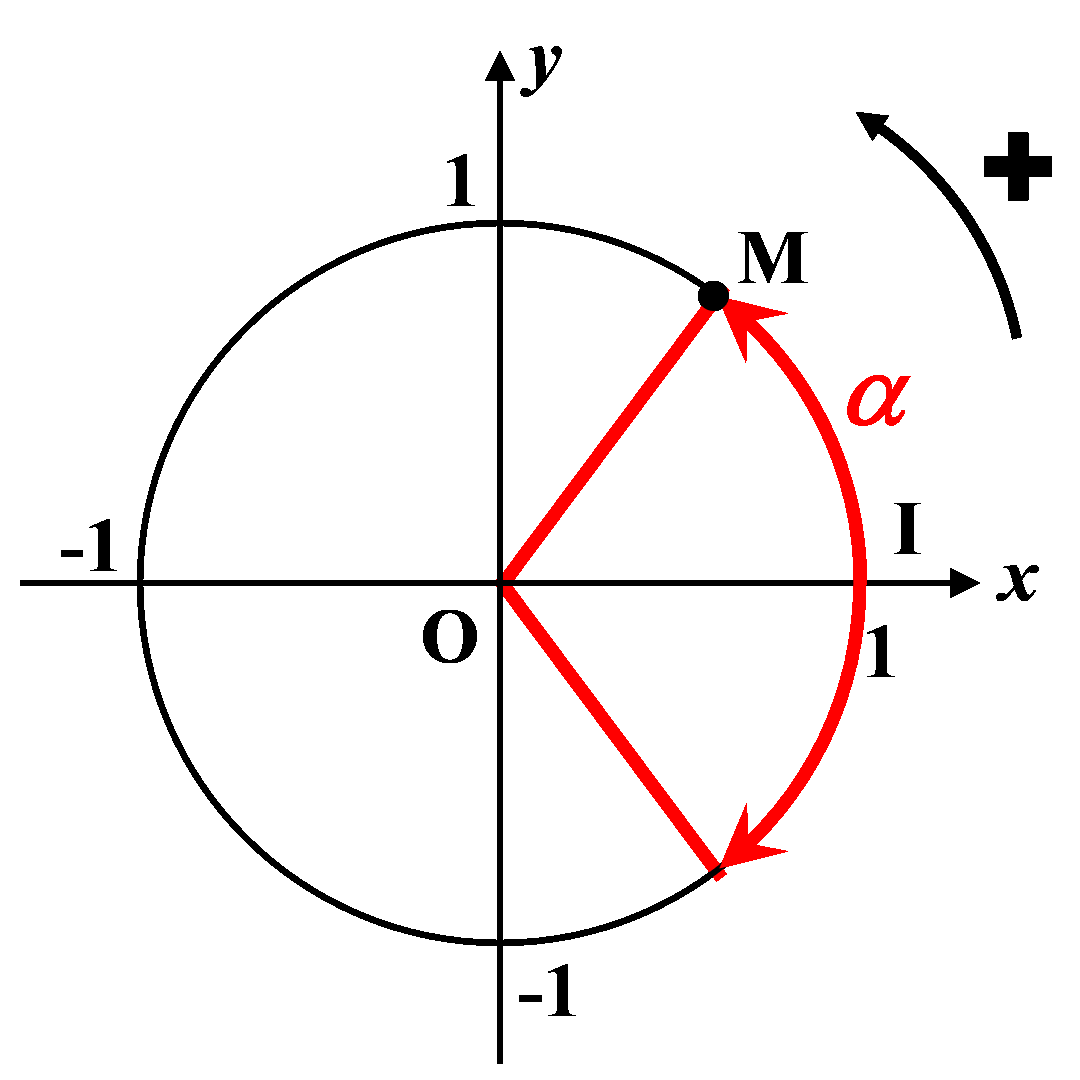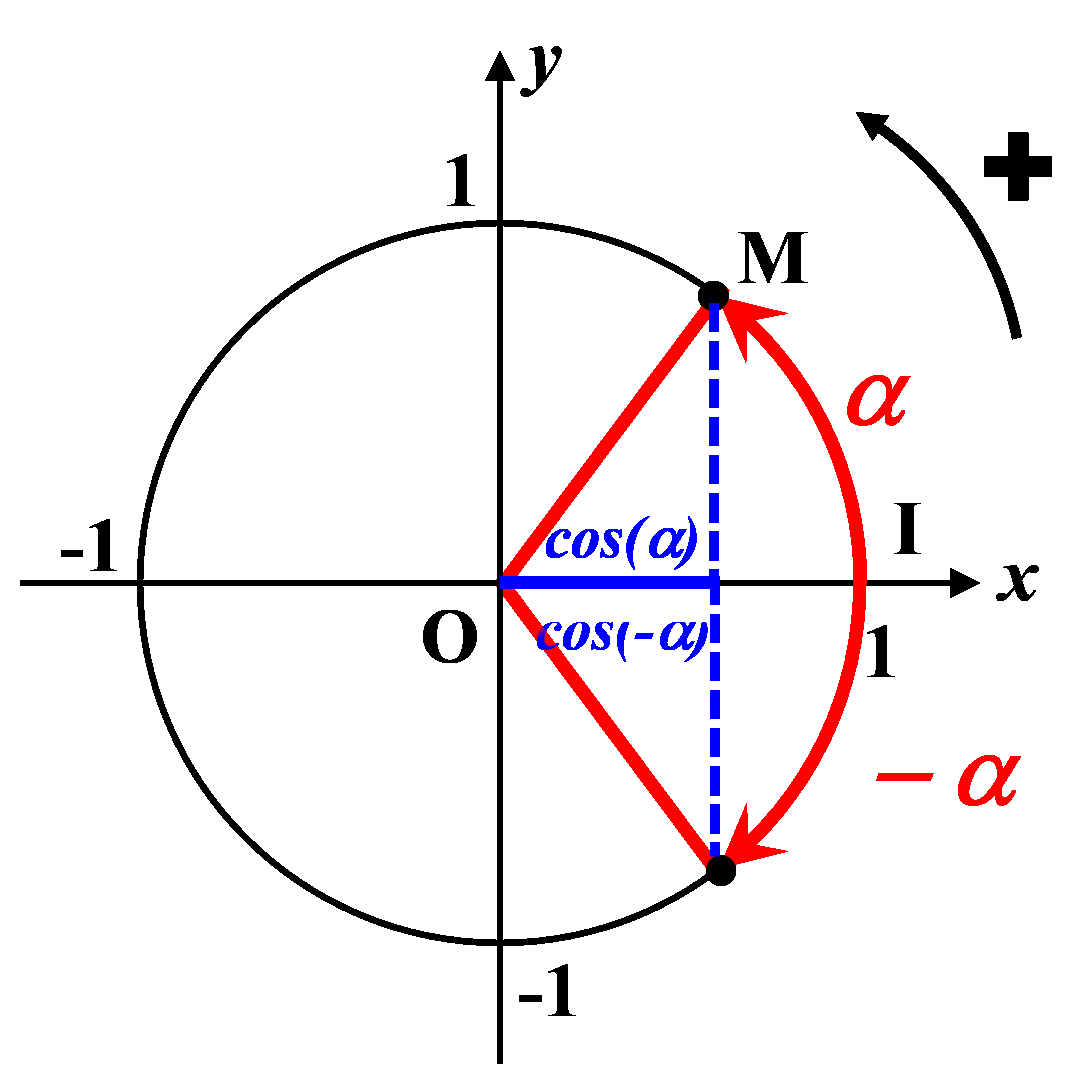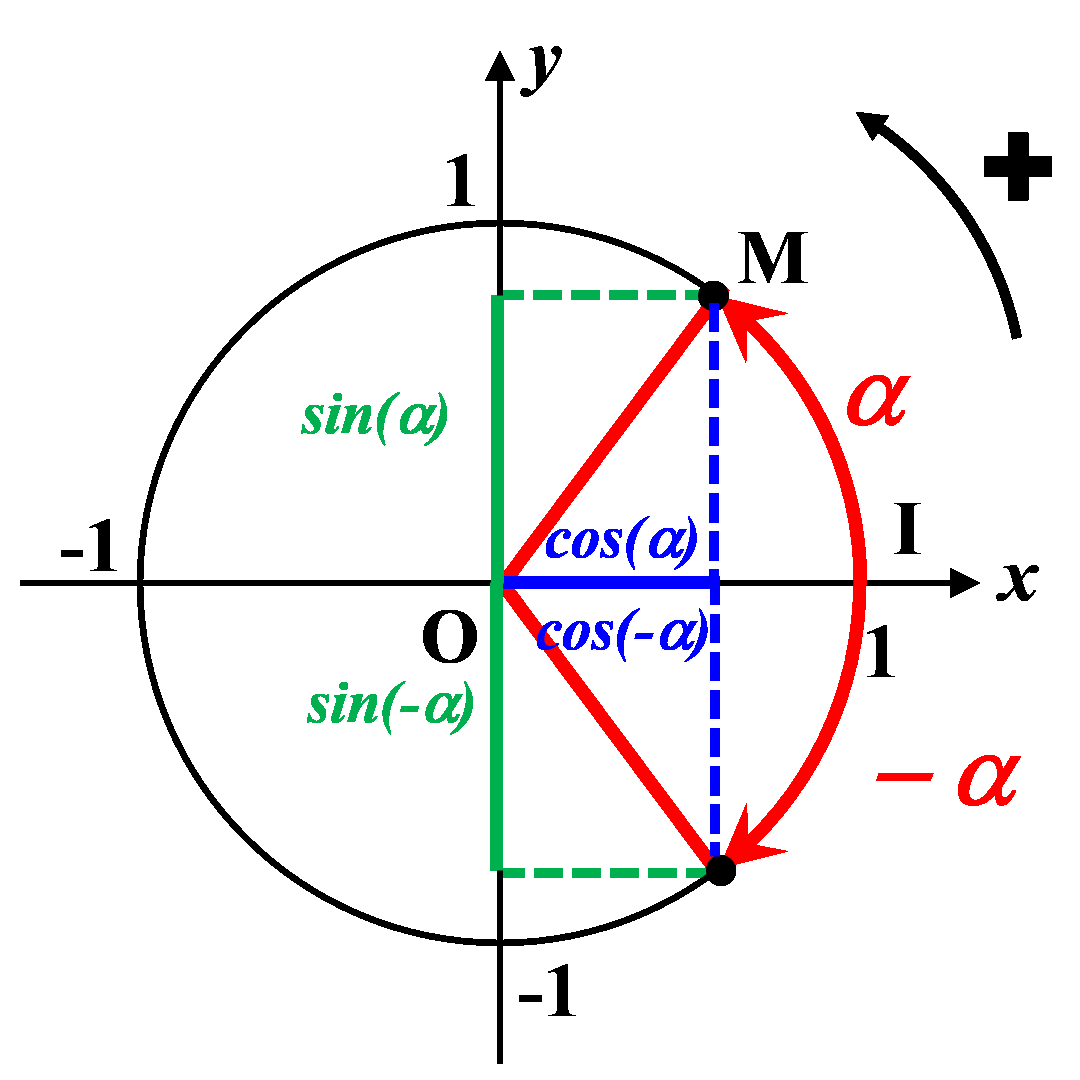 |
C42. Angles complémentaires.
|
$\bullet$ Deux sont dits "complémentaires" lorsque leur somme est égale à $\dfrac{\pi}{2}$. $\bullet$ Le sinus de l’angle complémentaire est égal au cosinus de cet angle. $sin \left (\dfrac{\pi}{2}-\alpha \right ) \ = \ cos(\alpha)$
$\bullet$ Le cosinus de l’angle complémentaire est égal au sinus de cet angle. $cos\left (\dfrac{\pi}{2}-\alpha \right ) \ = \ sin(\alpha)$ |
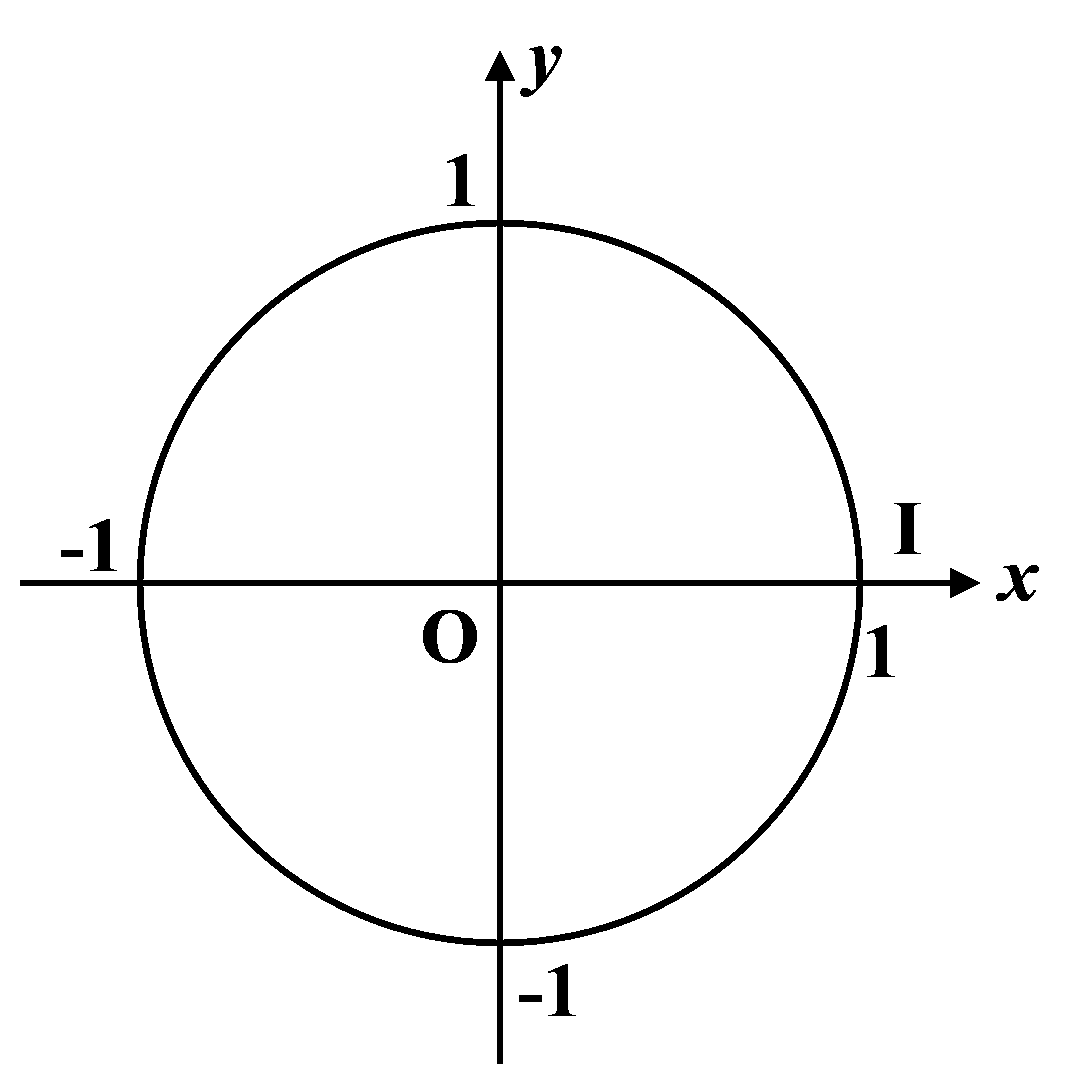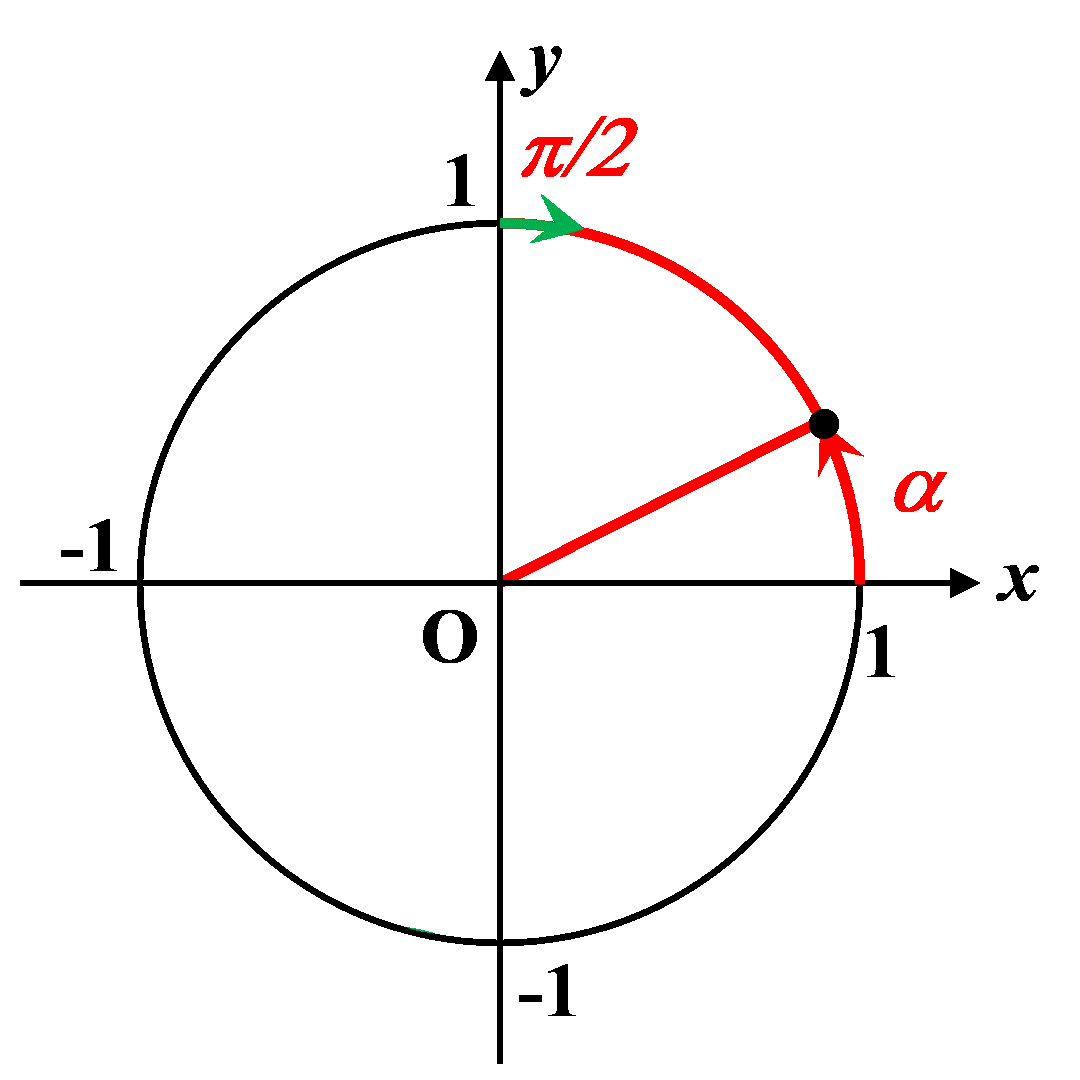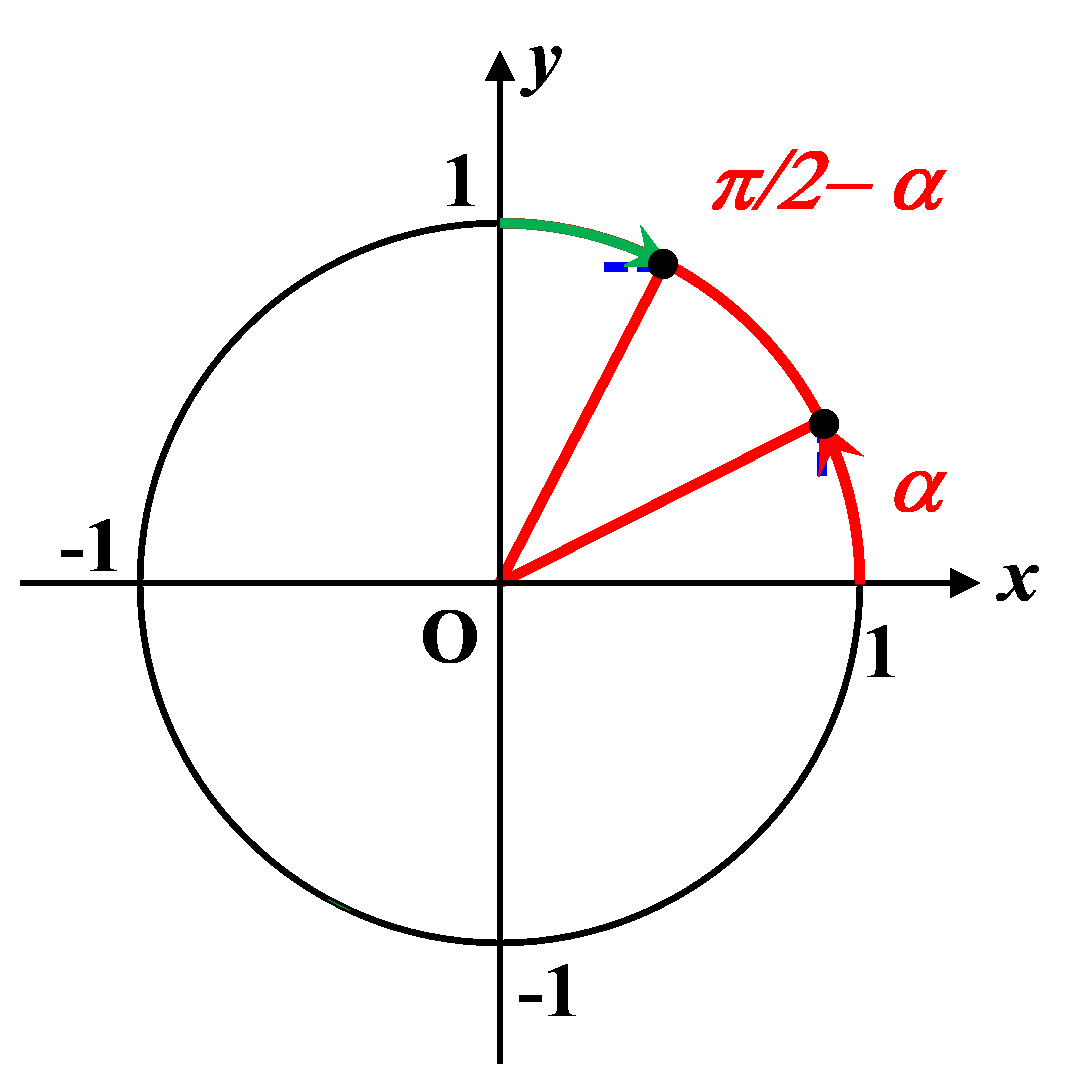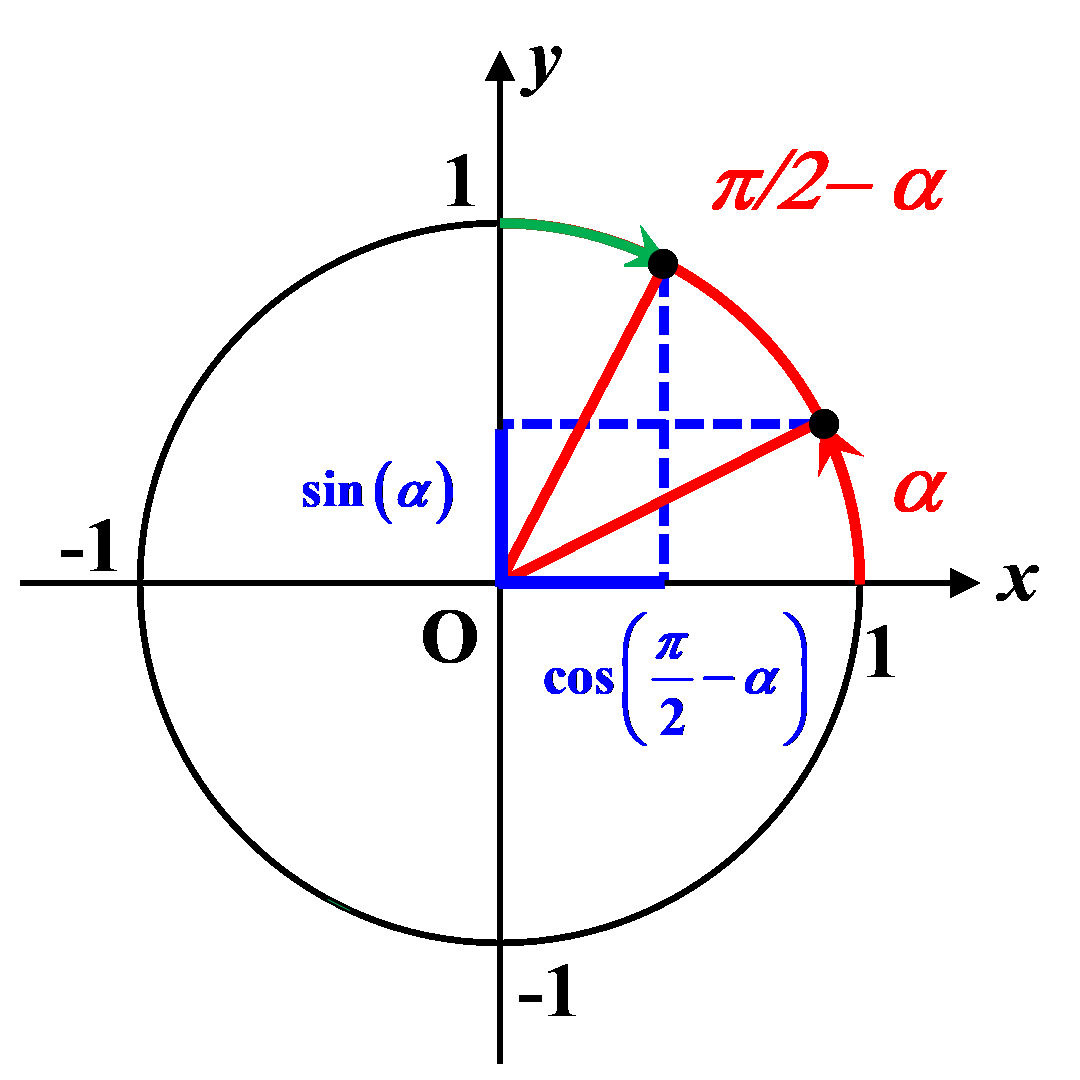 |
C43. Angles supplémentaires.
|
$\bullet$ Deux sont dits "complémentaires" lorsque leur somme est égale à $\pi$. $\bullet$ Les cosinus de deux angles supplémentaires sont opposés. $cos \left (\pi-\alpha \right ) \ = \ - \ cos(\alpha)$
$\bullet$ Les sinus de deux angles supplémentaires sont égaux. $sin \left (\pi-\alpha \right ) \ = \ sin(\alpha)$ |
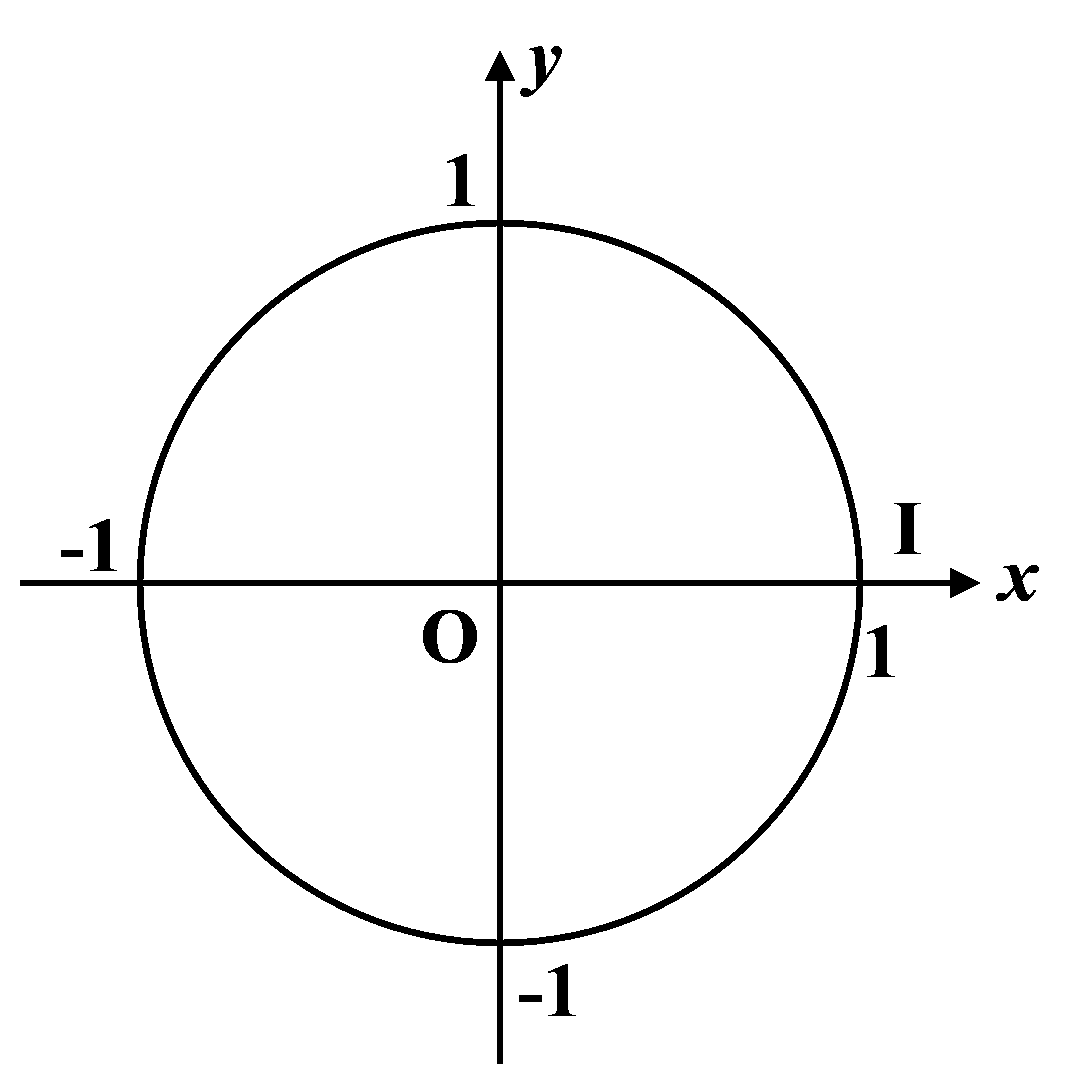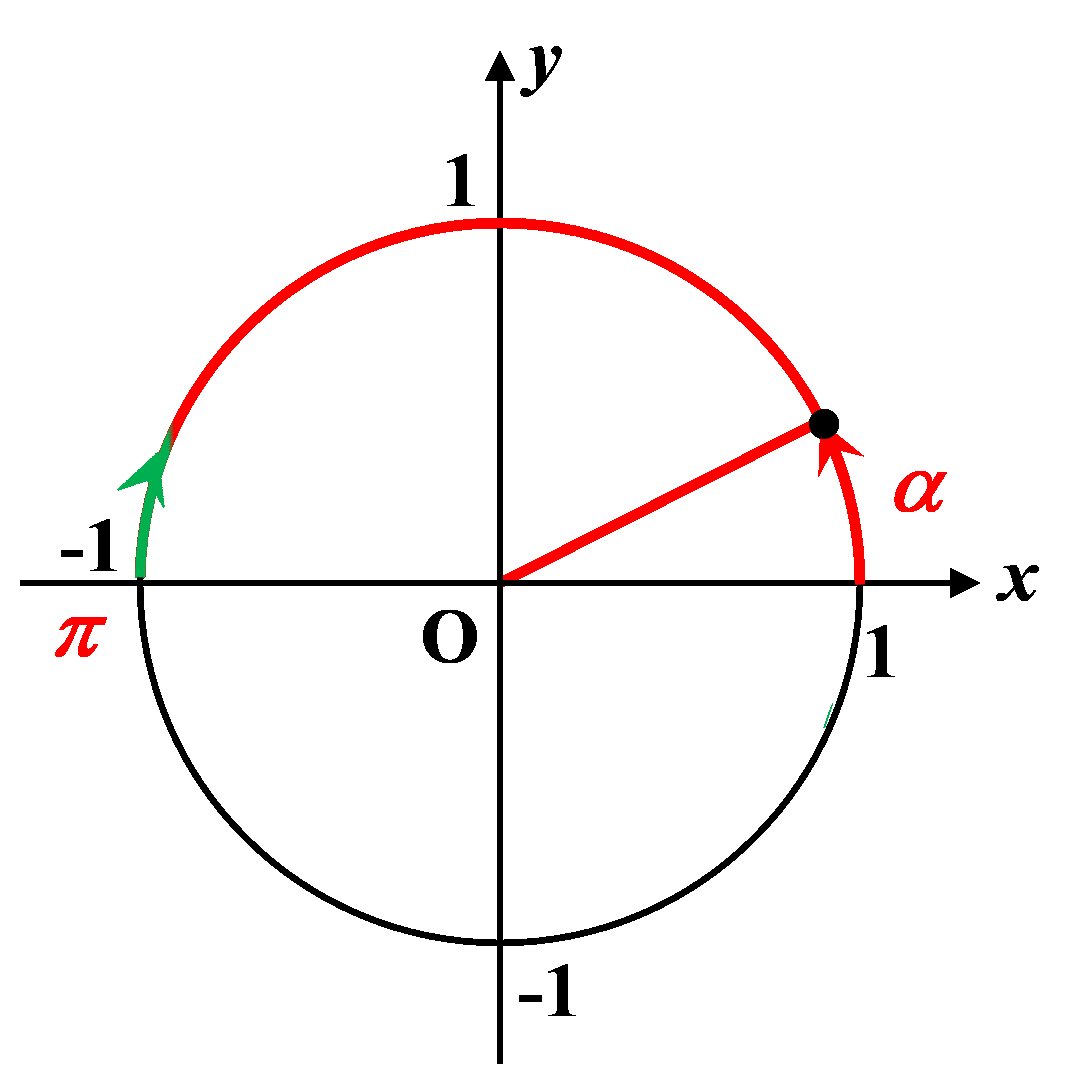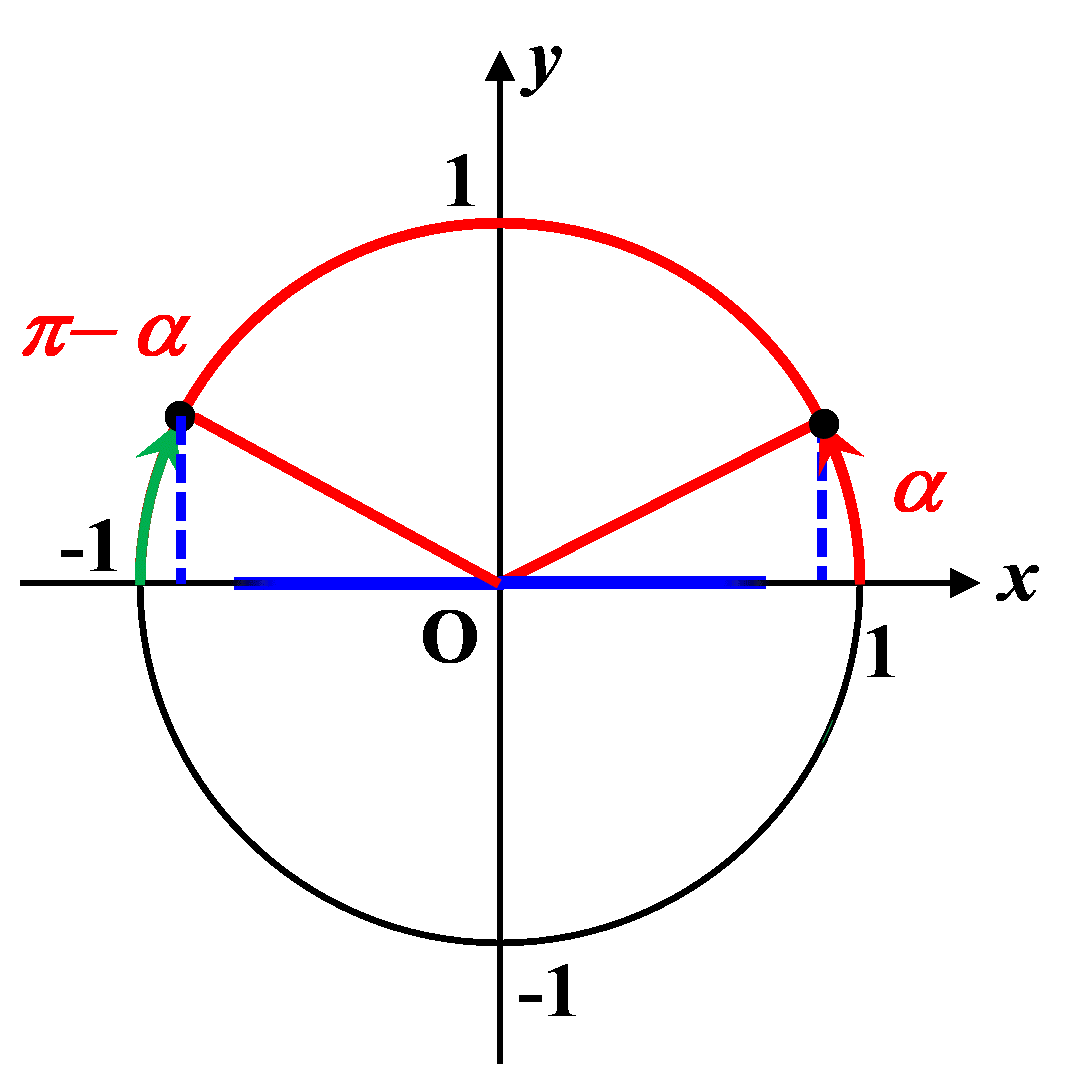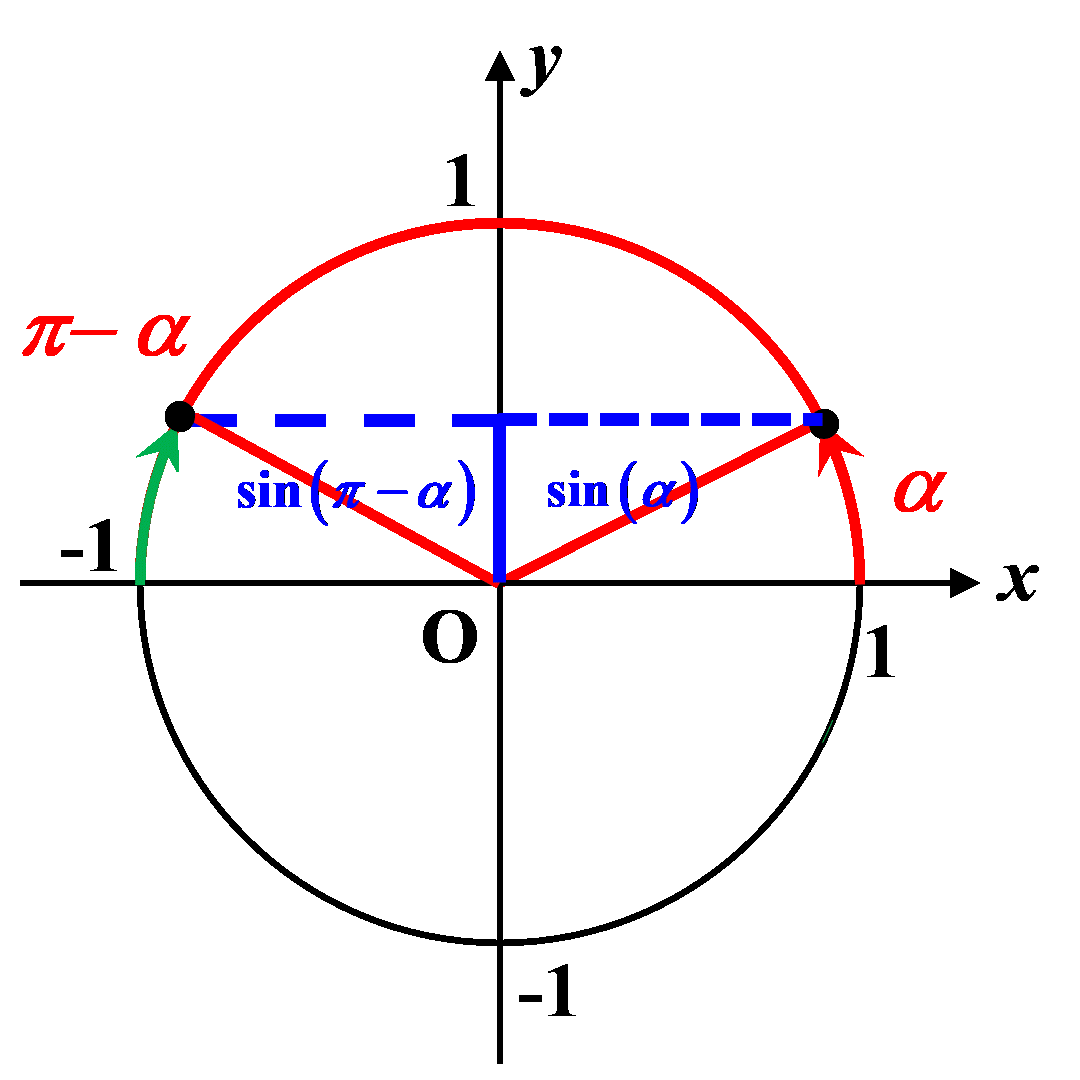 |
C44. Au-delà de $\dfrac{ \pi}{2}$.
|
$\bullet \ sin \left (\dfrac{\pi}{2}+ \alpha \right ) \ = \ - \ cos(\alpha)$
$\bullet \ cos\left (\dfrac{\pi}{2}+ \alpha \right ) \ = \ - \ sin(\alpha)$ |
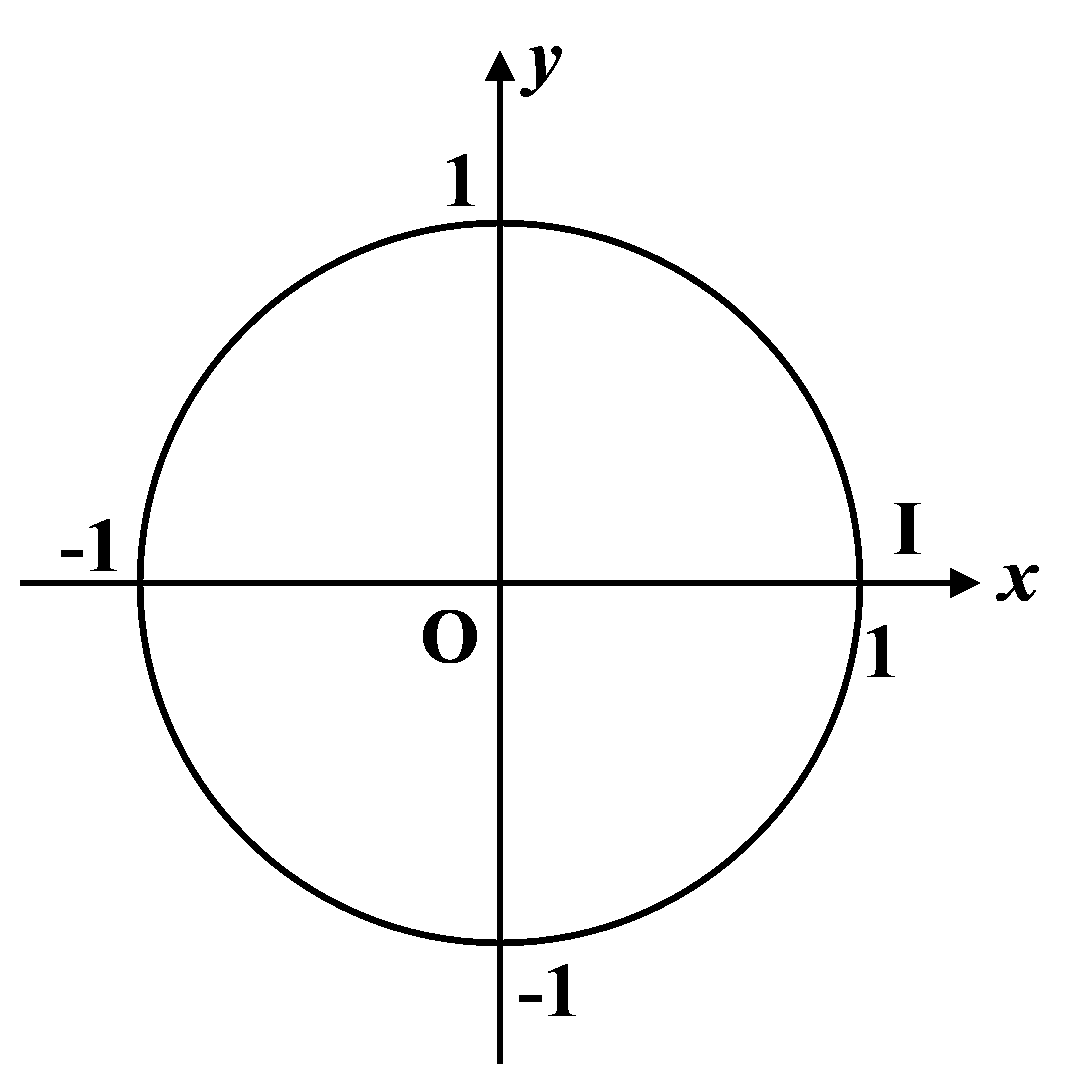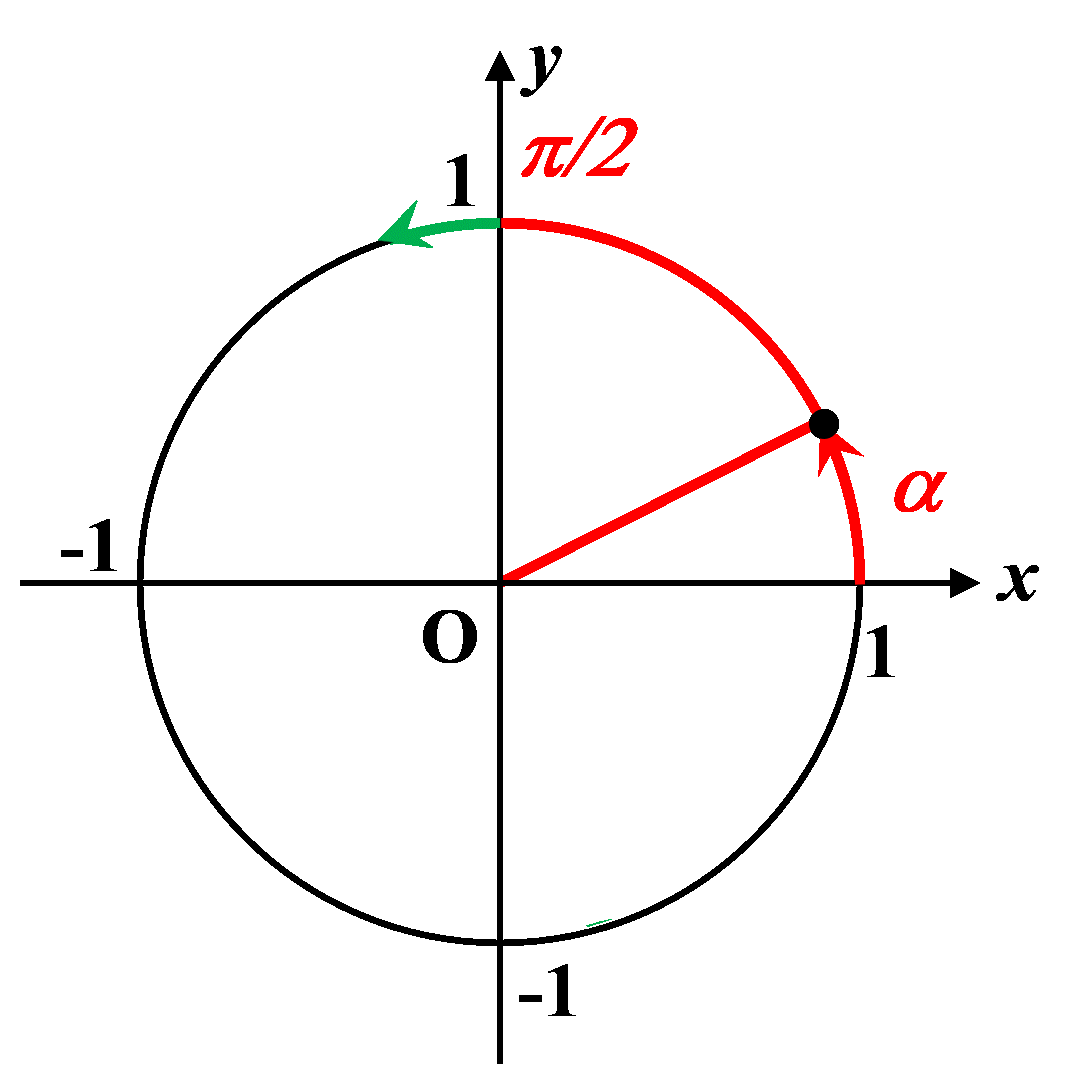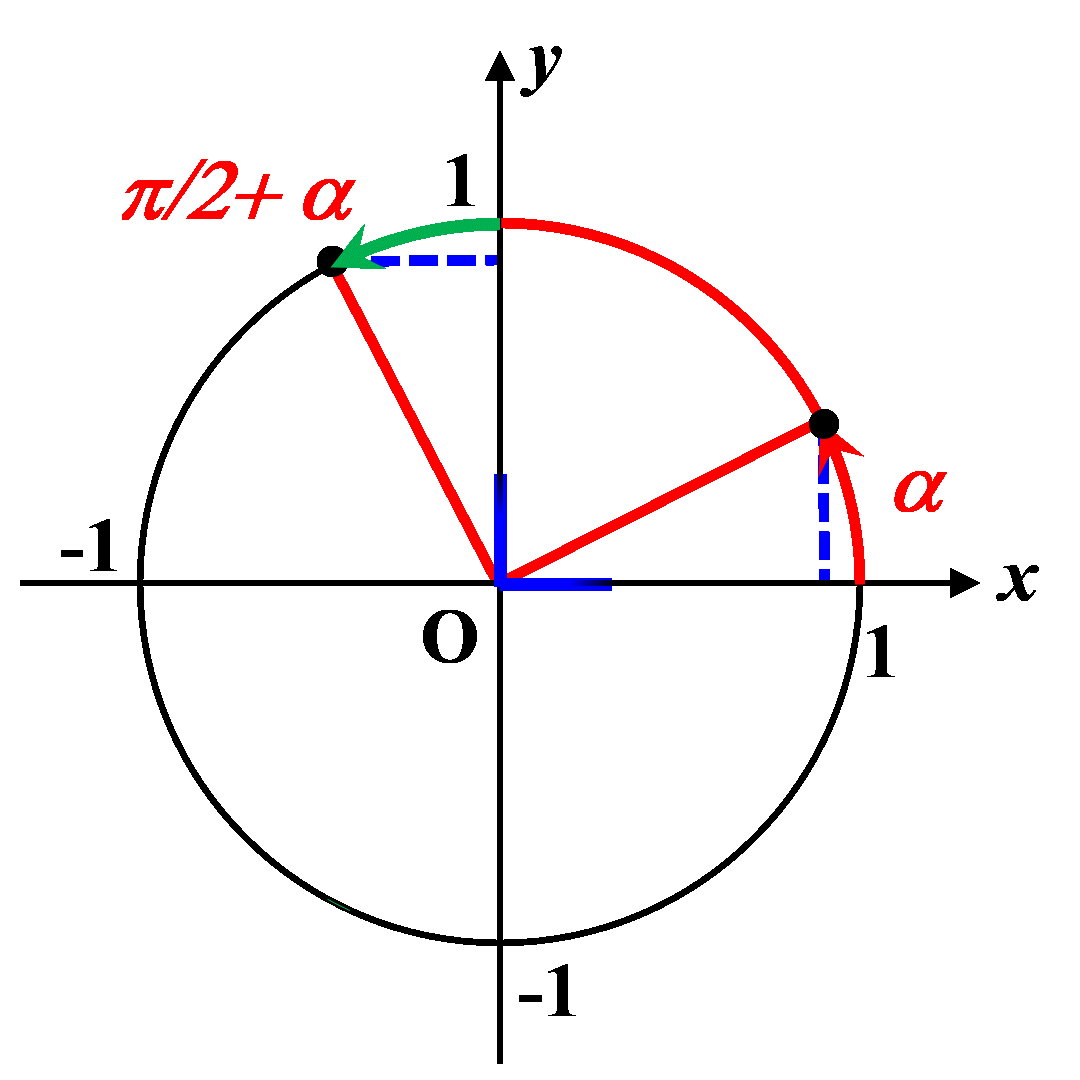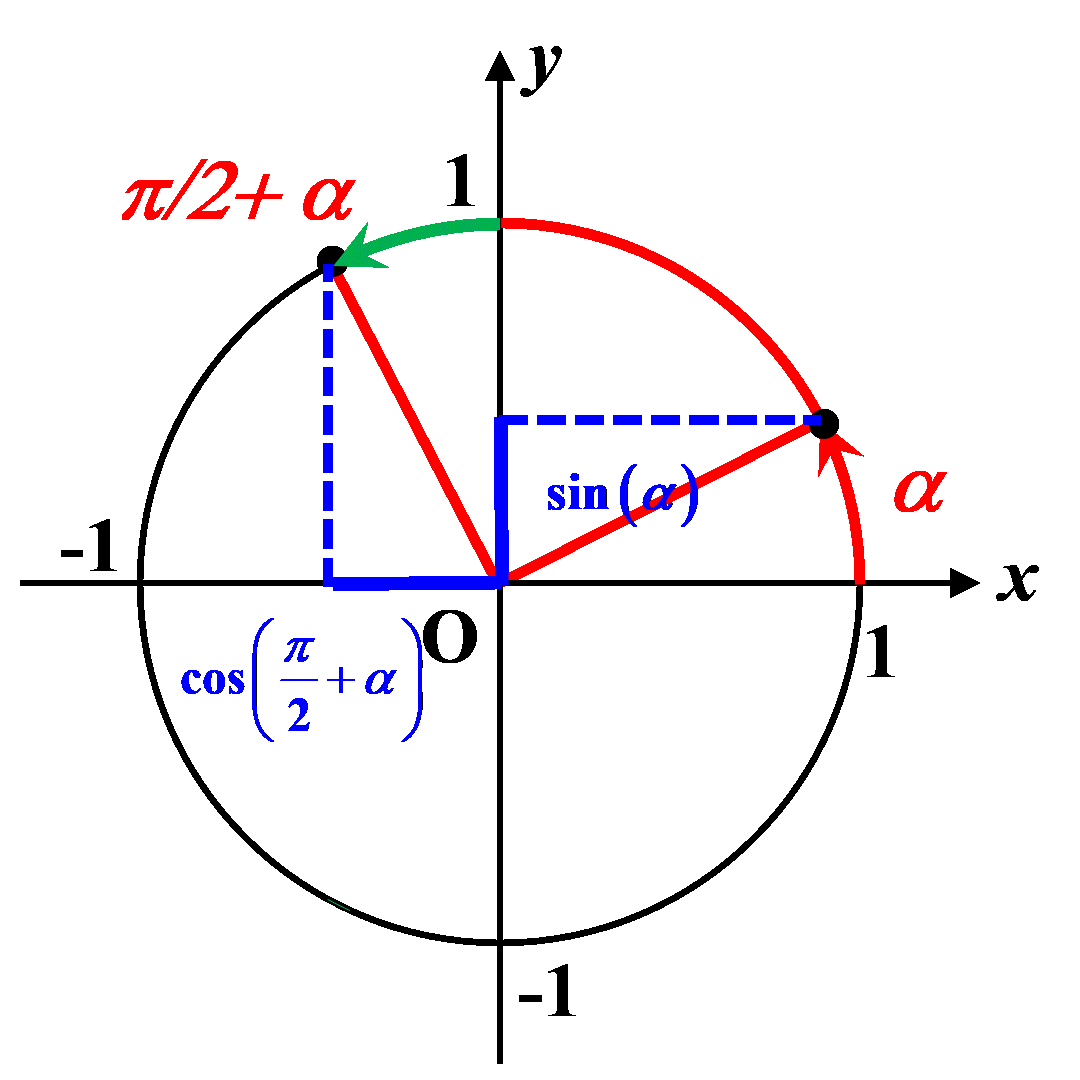 |
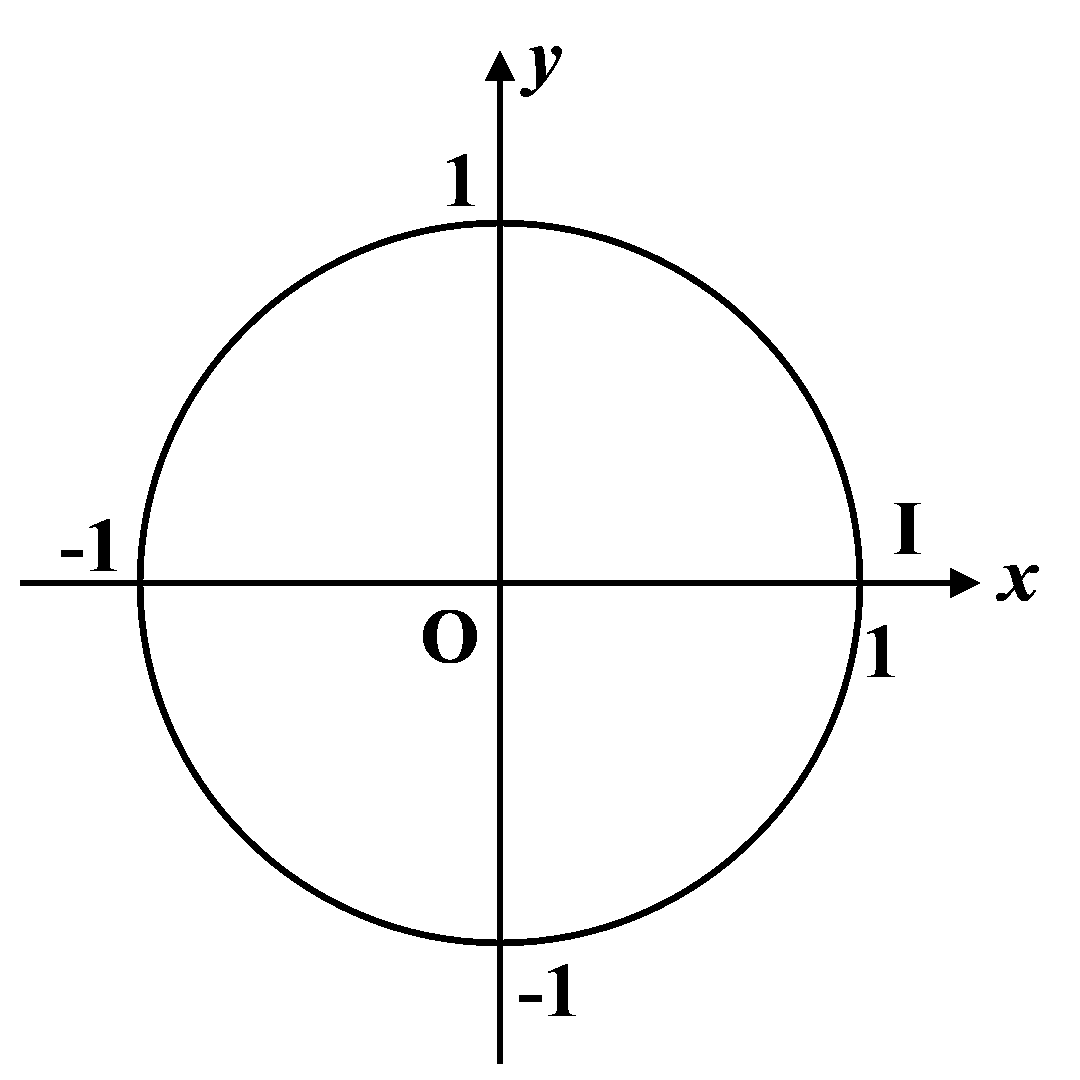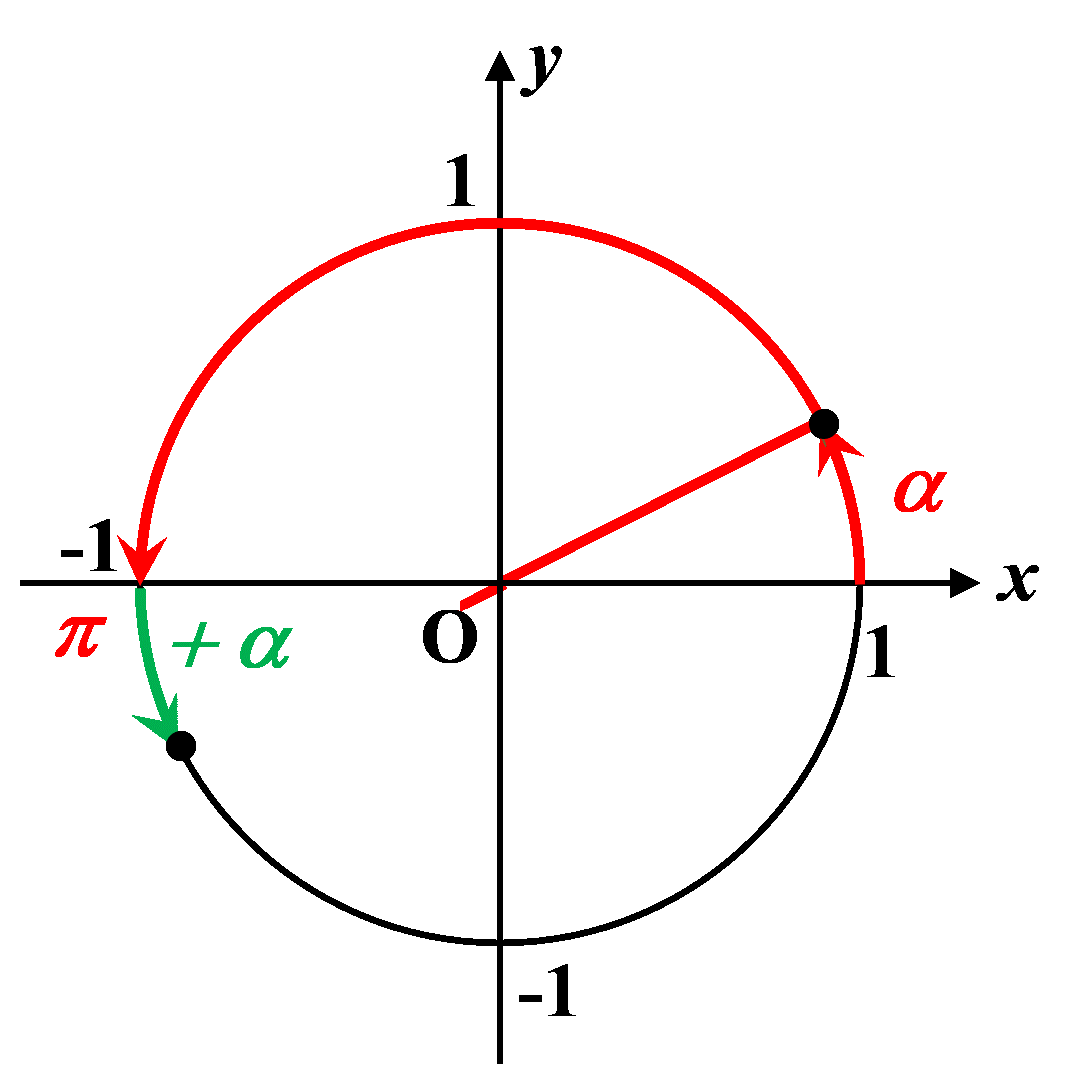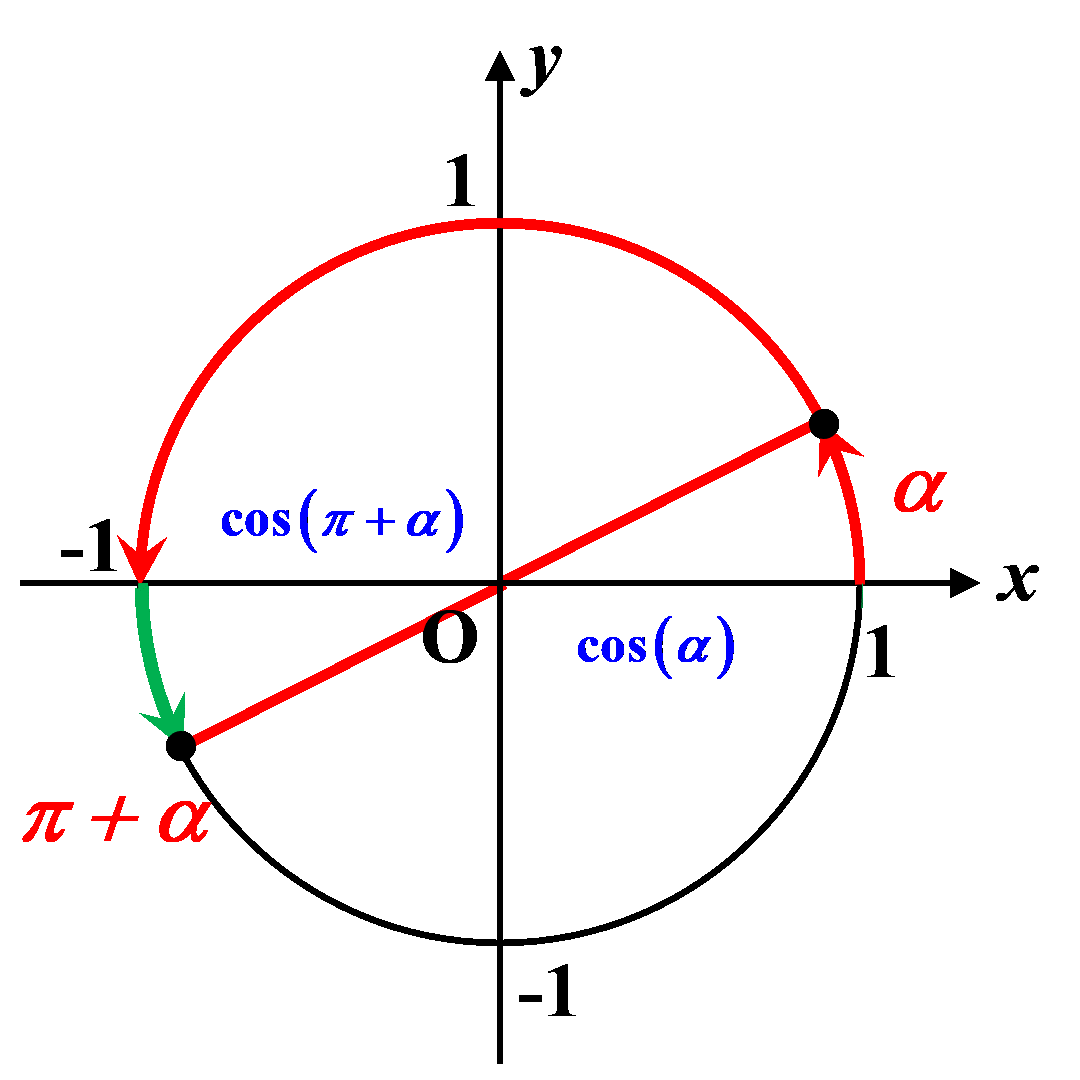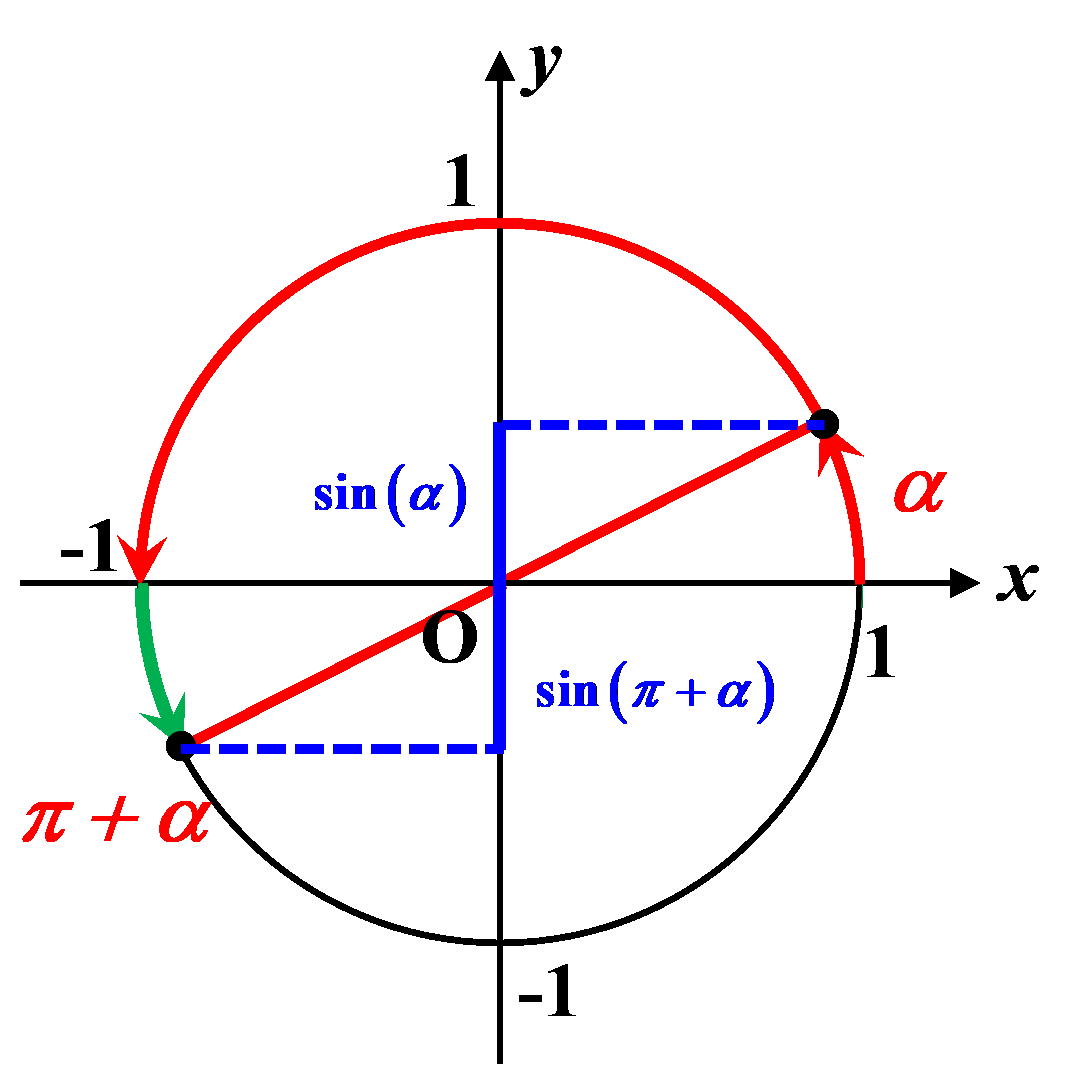
C44. Au-delà de $\pi$.
|
$\bullet \ cos \left (\pi + \alpha \right ) \ = \ - \ cos(\alpha)$
$\bullet \ sin \left (\pi + \alpha \right ) \ = \ sin(\alpha)$ |
 |
C5. Fonctions numériques.
C51. La fonction sinus.
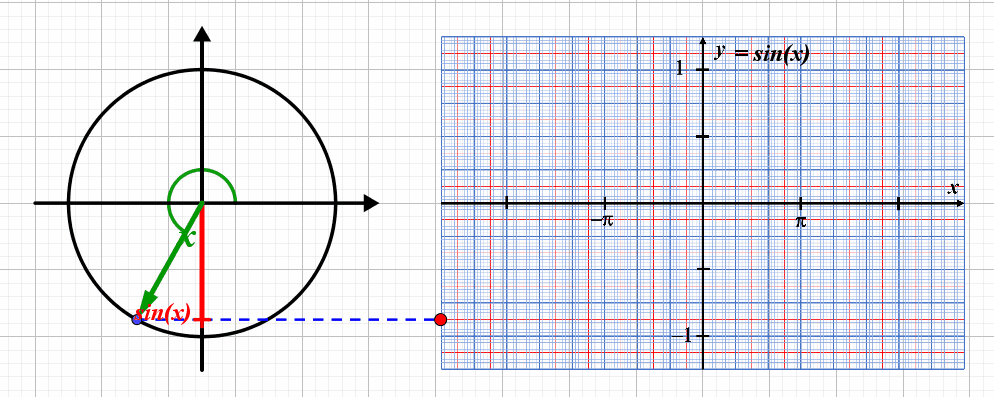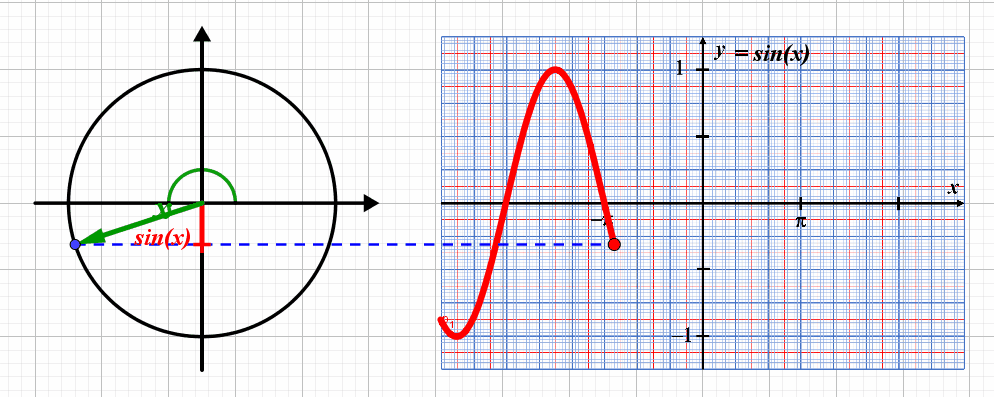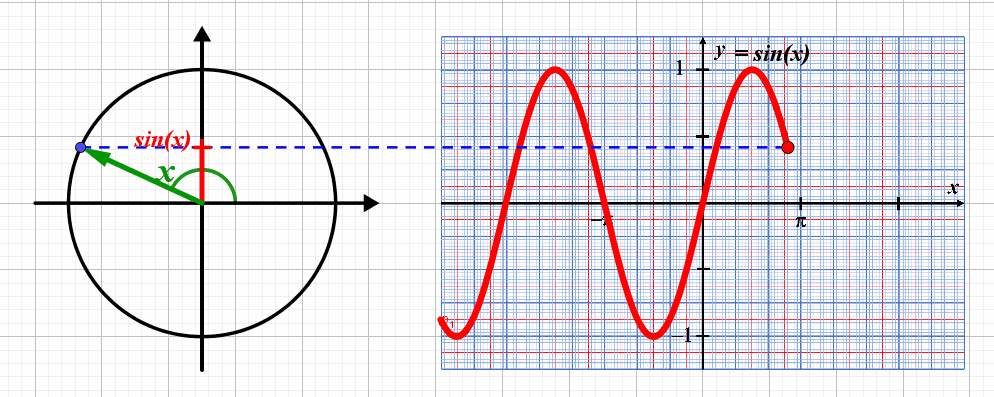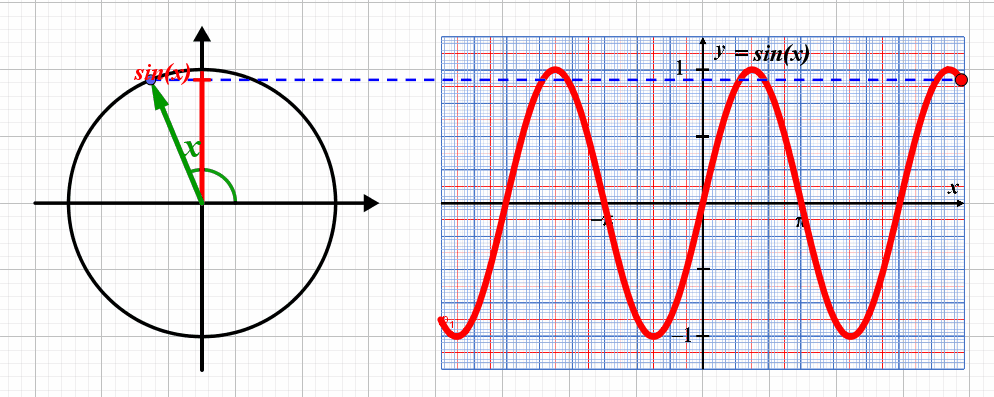
Lorsque le point correspondant au point de coordonnées $\left ( cos(x) \ ; \ sin(x) \right )$ , la valeur du sinus varie entre les valeurs $-1$ et $+1$ : la fonction a une amplitude égale à $1$.
La courbe représentative se répète tous les $2 \pi$ : la fonction $x \mapsto sin(x)$ est $2 \pi$-périodique.
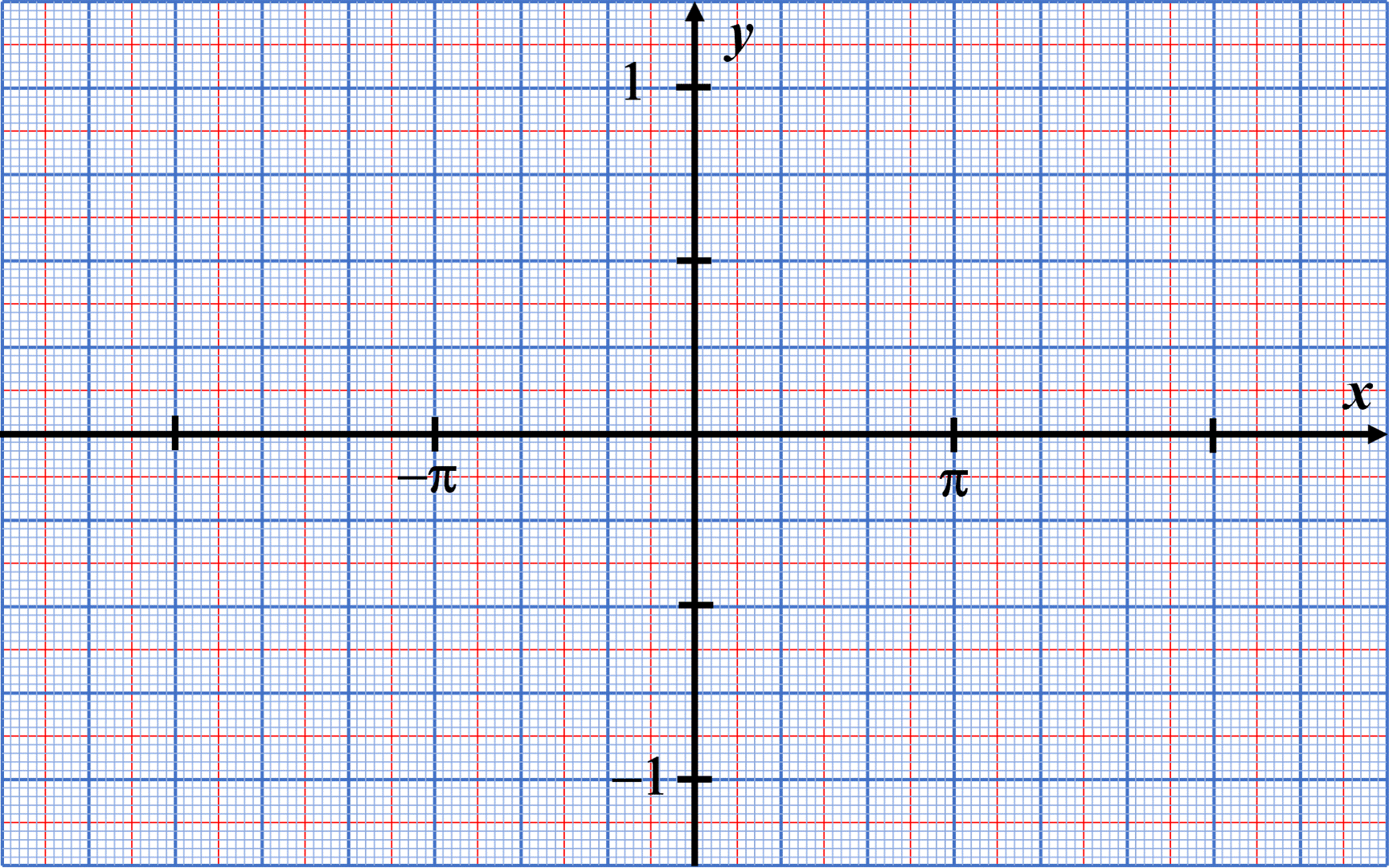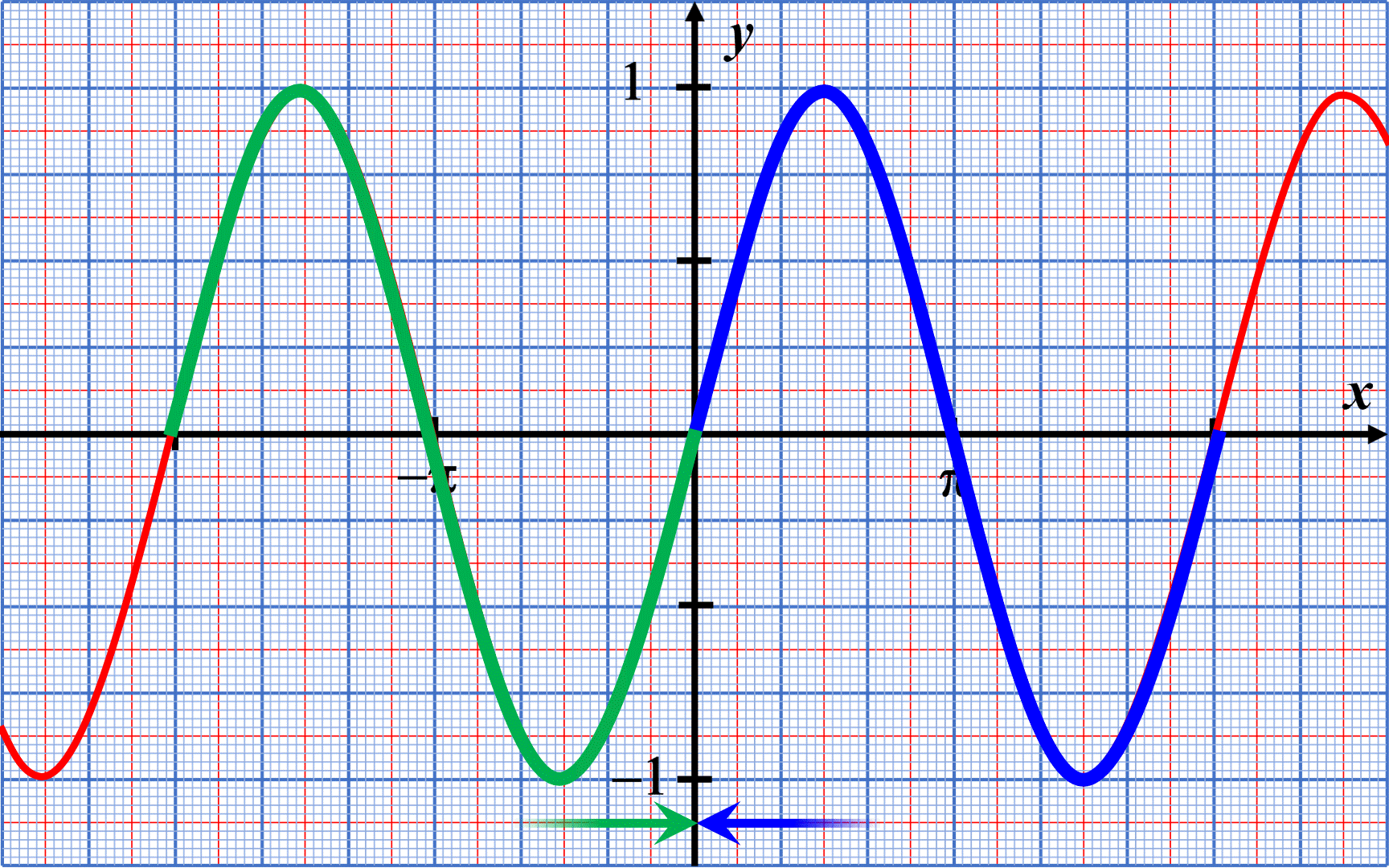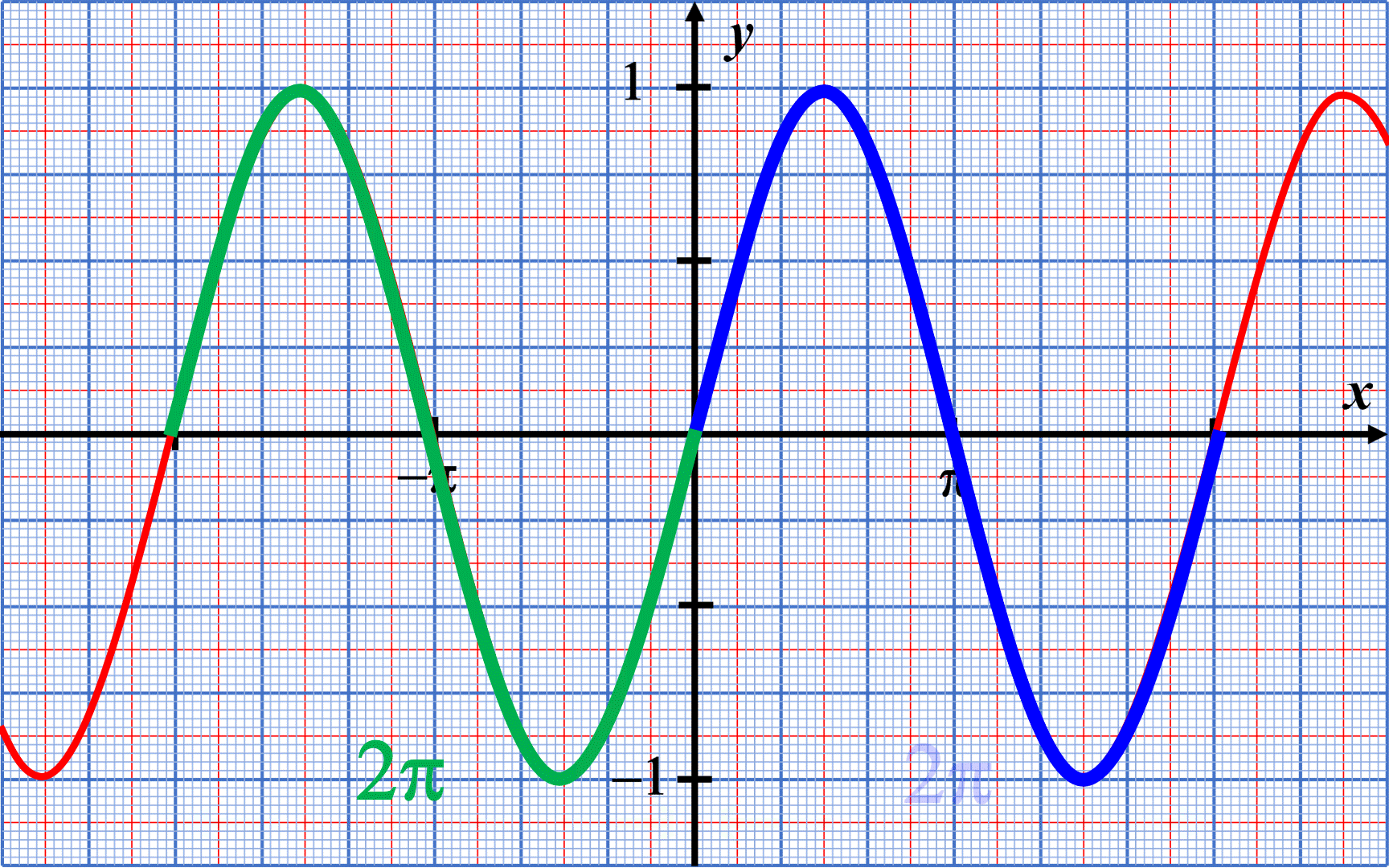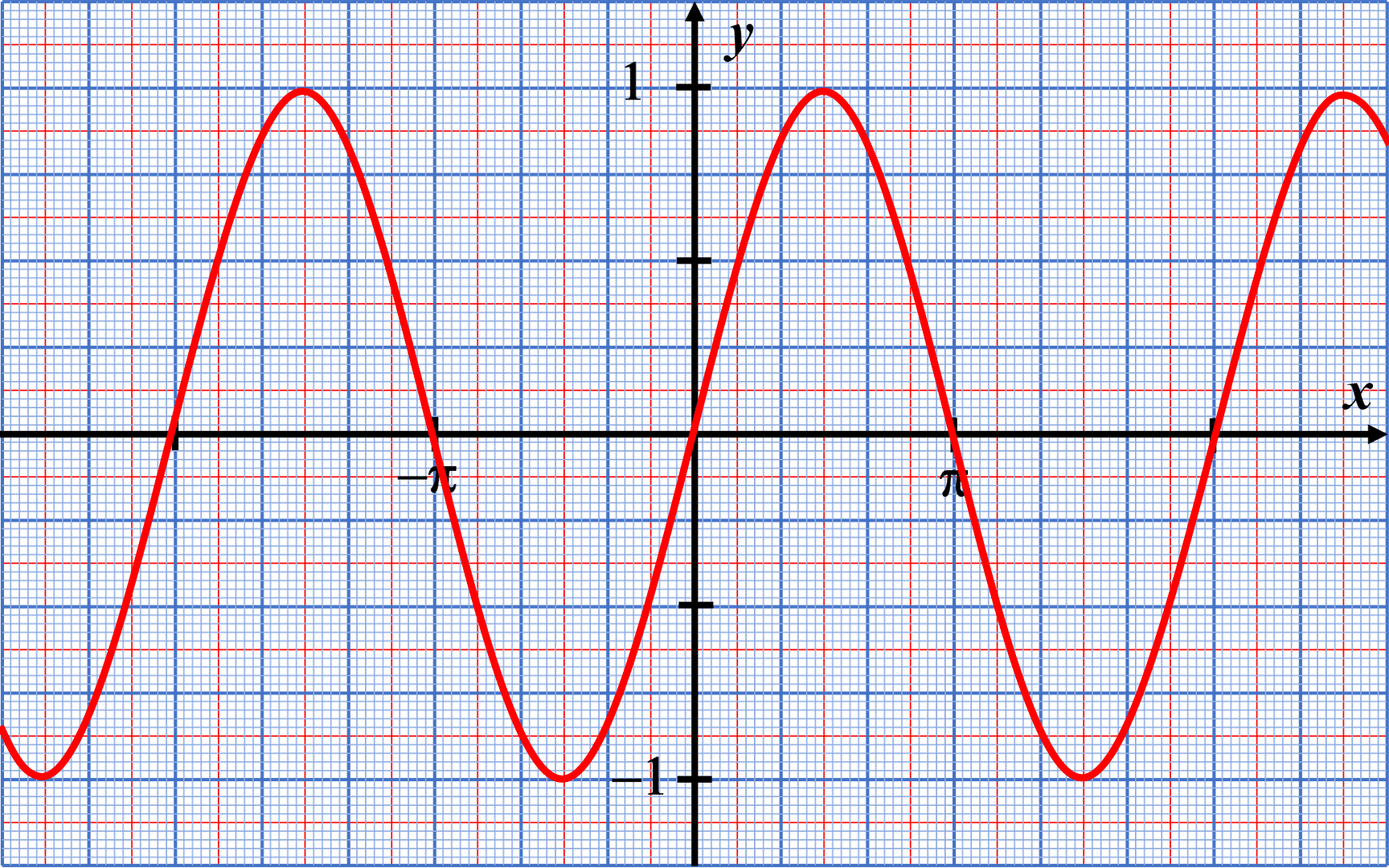
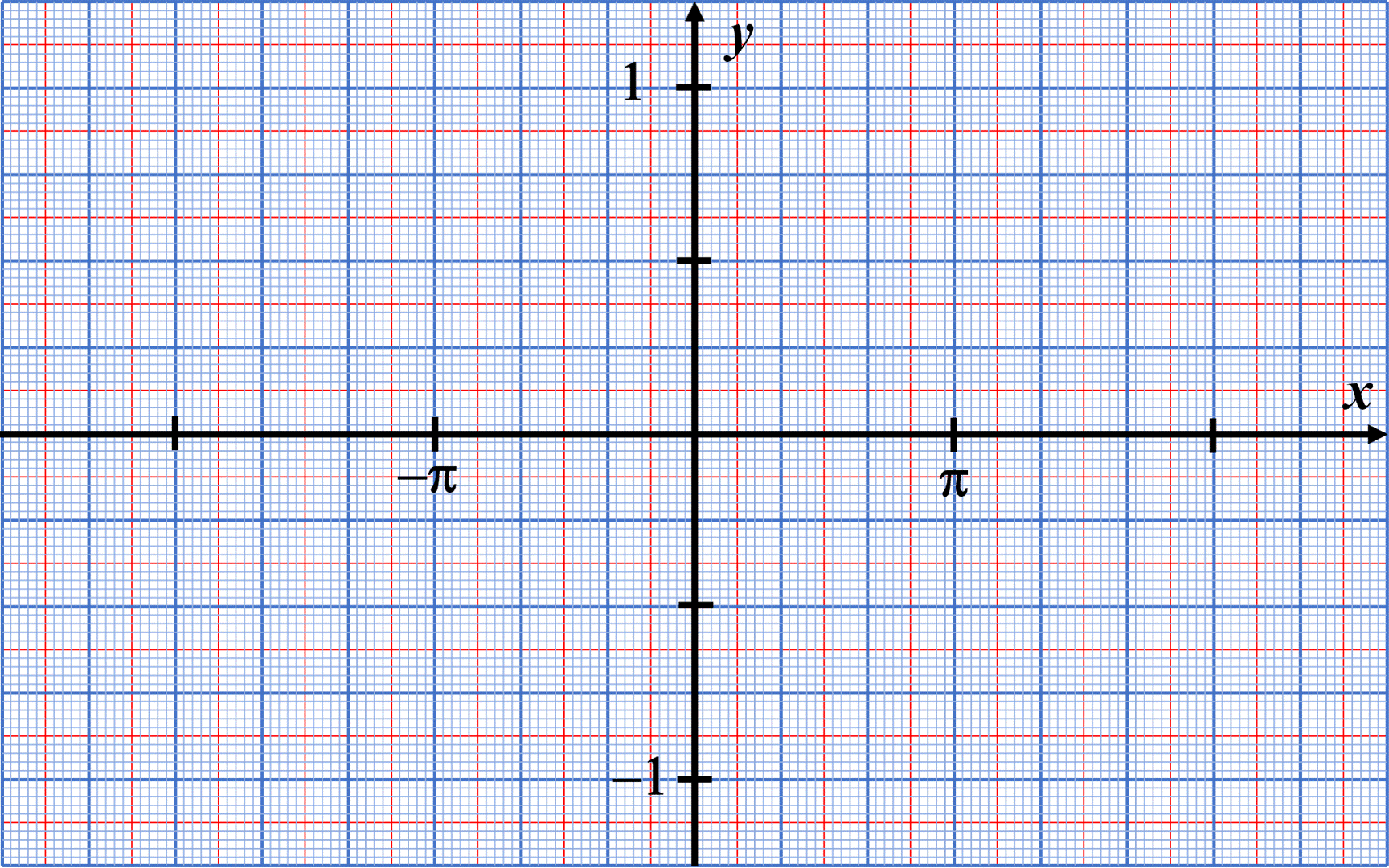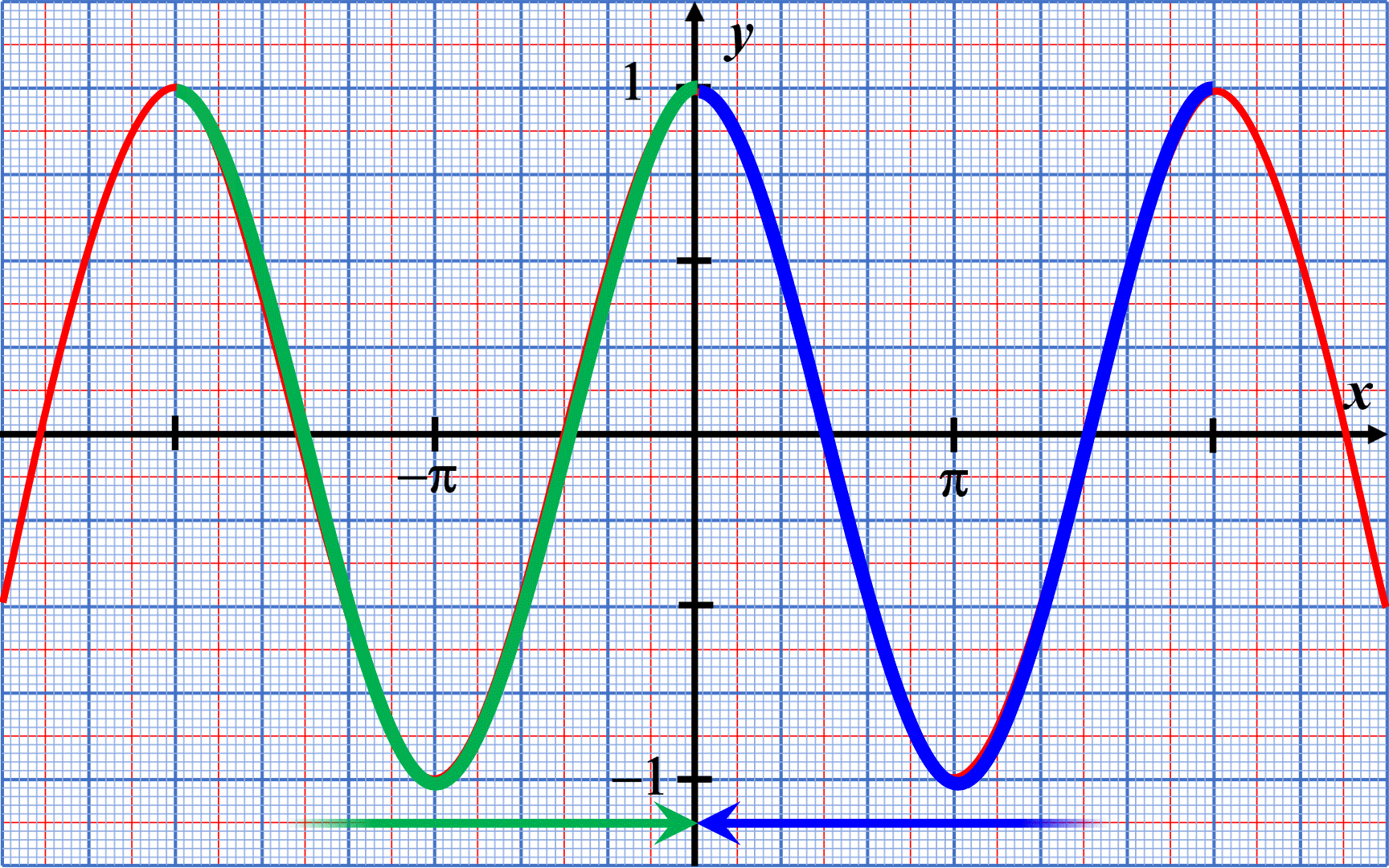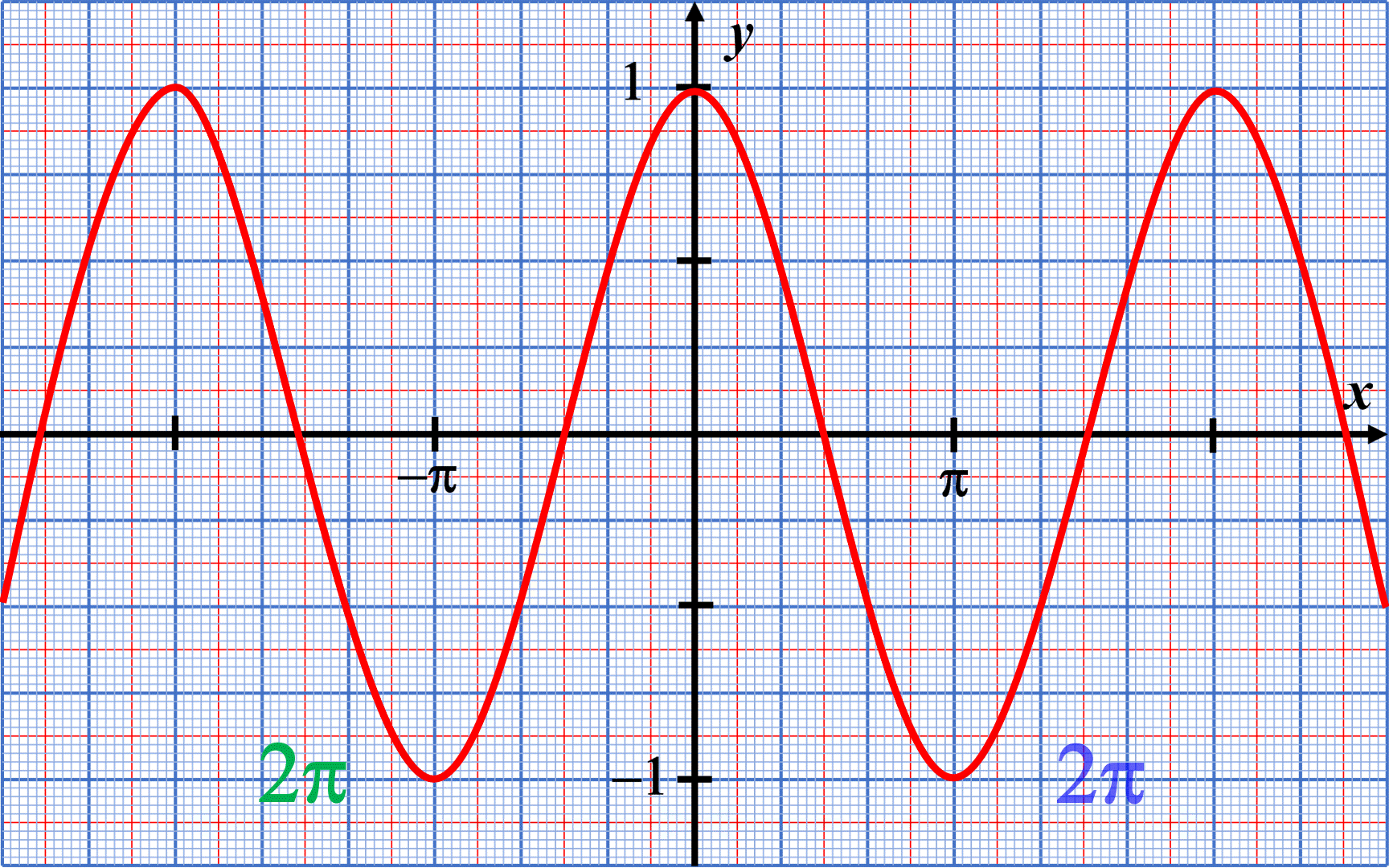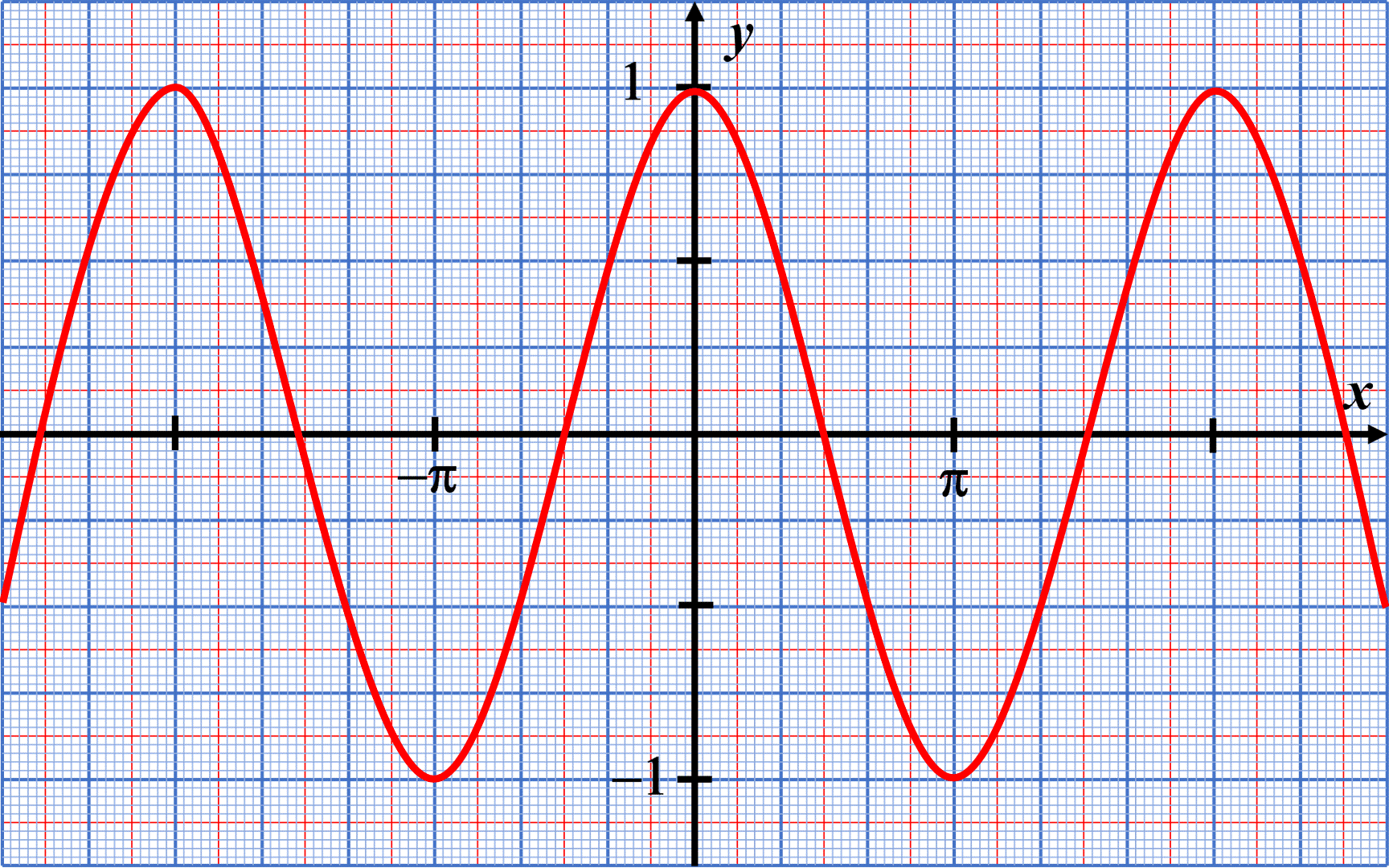
C52. La fonction cosinus.
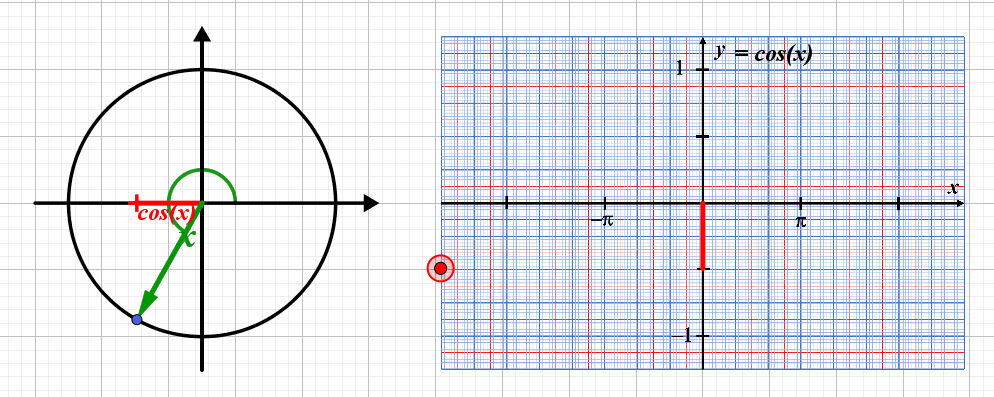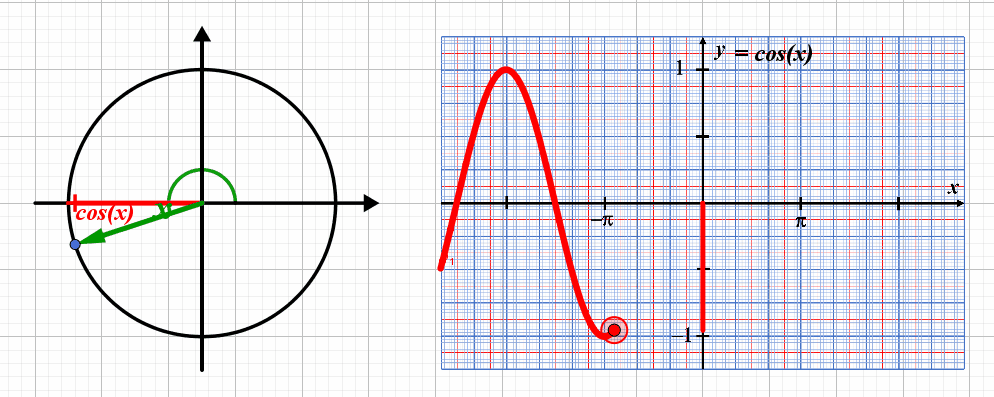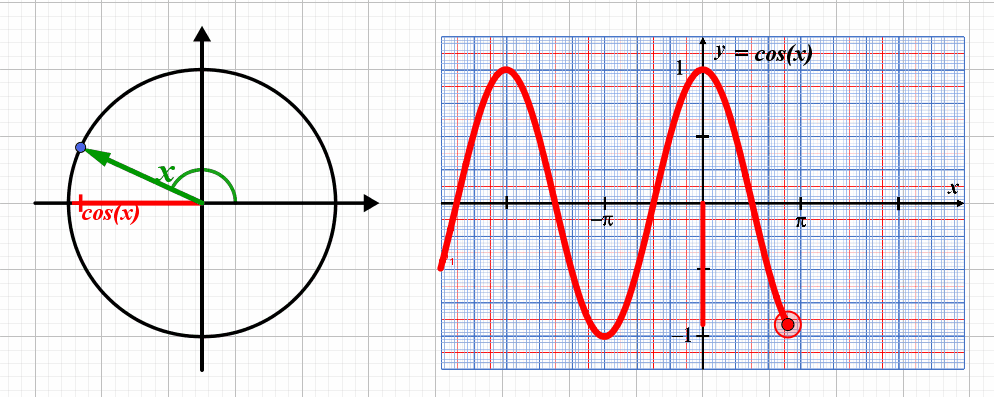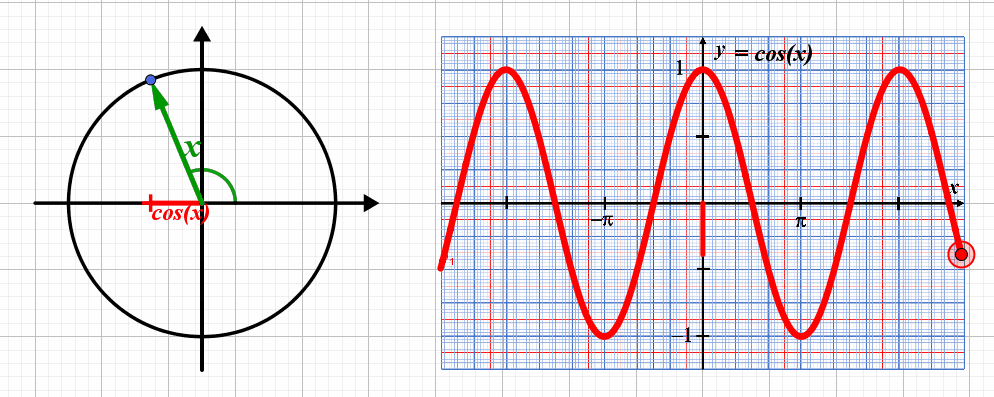
Lorsque le point correspondant au point de coordonnées $\left ( cos(x) \ ; \ sin(x) \right )$ , la valeur du sinus varie entre les valeurs $-1$ et $+1$ : la fonction a une amplitude égale à $1$.
La courbe représentative se répète tous les $2 \pi$ : la fonction $x \mapsto cos(x)$ est $2 \pi$-périodique.
Ajouter un commentaire