2ème Loi de Newton
ACTIVITES
A1 : Centre de masse d'un système.
Lorsqu’on décrit le mouvement d’un système et les actions mécaniques qui s’exercent sur lui, nous réduisons le système à un point G appelé centre de masse.
Comment localiser ce point ou comment justifier sa position si elle nous est donnée ?
|
|
|
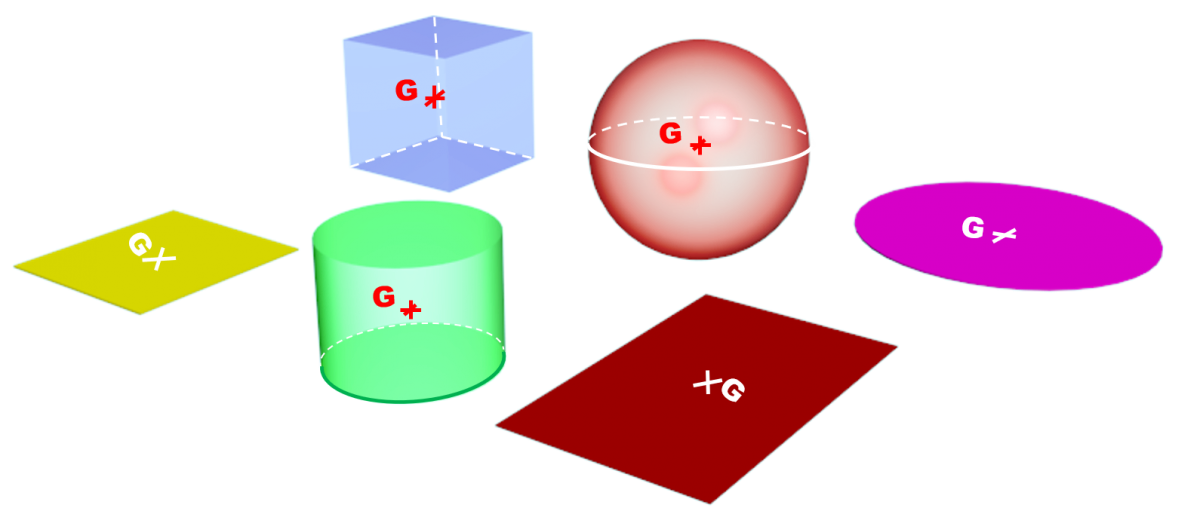
• Mettre en œuvre le dispositif expérimental du doc 2.
• Comparer les positions des centres de masse G pour chaque objet.
• Que peut-on en déduire de la position du centre de masse de l'objet par rapport à sa forme ?
• Comparer les trajectoires du centre de masse G et des autres points du système.
• Que peut-on en déduire de la trajectoire du centre de masse ?
• Comment peut-on justifier la position du centre de masse d'un système ?
• Estimer la position du centre de masse du marteau en expliquant votre démarche.
A1 : Référentiel galiléen.
Un référentiel est un objet par rapport auquel on étudie le mouvement d'un autre objet. Il est dit "galiléen" si les lois de la Physique de Newton s'y appliquent.
Tous les référentiels qui nous entourent sont-ils galiléens ?
|
|
|
Doc 4 : Principe d’inertie ou 1re loi de Newton Dans un référentiel galiléen, tout corps persévère dans son état de repos ou de mouvement rectiligne uniforme si les actions mécaniques qui s’exercent sur lui se compensent. |
• Que peut-on dire des forces qui modélisent les actions mécaniques exercées sur le mobile autoporteur ?
• Quel est le référentiel d’étude dans le cas du document 2 ? Décrire le mouvement du système dans ce cas.
• Quel est le référentiel d’étude dans le cas du document 3 ? Décrire le mouvement du système dans ce cas.
• Qu’est-ce qu’un référentiel galiléen ? Donner des exemples.
A3 : Deuxième loi de Newton.
La deuxième loi de Newton permet de relier le mouvement d’un système et les forces qui s’exercent sur lui.
Objectif : Utiliser la deuxième loi de Newton pour déterminer la norme d’une force.
|
Doc 1 : Protocole du mouvement d'un objet sur un plan incliné.
|
|
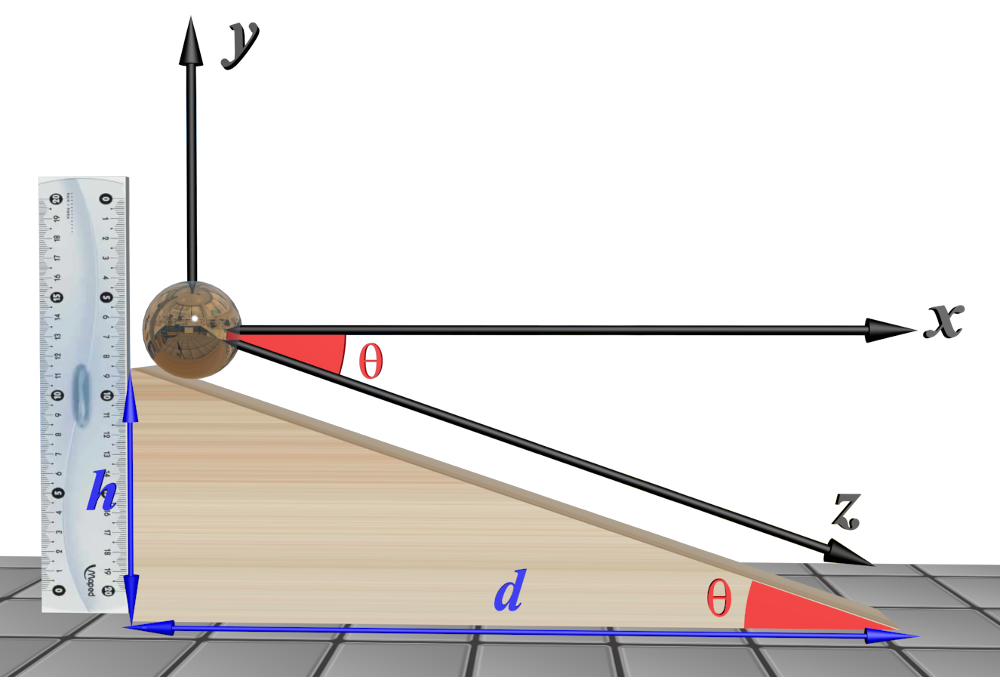
Doc2 : schéma. |
• Mise en place :
- Mesurer la masse du mobile : ……………………………………………
- Mesurer l'angle d'inclinaison du plan : ……………………………………………
- Positionner la règle qui servira d'étalon : ……………………………………………
- Filmer, pointer.
• Faire le bilan des forces s'exerçant sur le mobile (on négligera les frottements de l'air), les frottements sur le support seront modélisés par une force constante $\vec f $ .
• Représenter ces forces sur le schéma ci-dessous.
• Utiliser la 2ème loi de Newton pour montrer que la coordonnée az de l'accélération sur l'axe (Oz) s'écrit :
$ a_{z} = -g \times sin \theta - \dfrac {f}{m} $ .
• En déduire l'équation horaire de la position z(t) :
• Comparaison avec la théorie :
- Y a-t-il adéquation entre la théorie est l'expérimentation ?
- En considérant que le modèle est valide, déterminer la valeur de la norme f de la force de frottement.
• Expliquer comment la deuxième loi de Newton peut être utilisée pour calculer la norme d’une force.
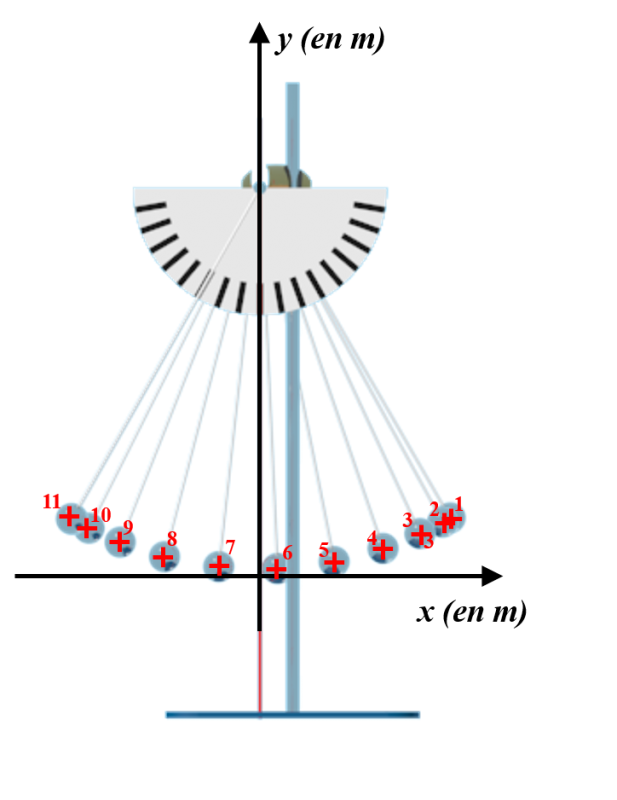
A4 : Mouvement d'un pendule.
|
Un pendule simple suit un mouvement de rotation autour de son point d'accroche.
La deuxième loi de Newton permet de comprendre son mouvement. |
 |
|
|
• Calculer les valeurs des vitesses aux points 4, 5, 8 et 9:
• Tracer les vecteurs variation de vitesse aux points 4 et 8 :
• Calculer les valeurs des accélérations aux points 4 et 10, puis les normes des vecteurs $m.\overrightarrow {a_{4}}$ et $m.\overrightarrow {a_{8}}$ .
• Tracer ces vecteurs en précisant l'échelle choisie.
• Calculer la norme du poids $\vec P $ . En utilisant la même échelle que celle choisie précédemment, tracer le poids aux points 4 et 8.
• En utilisant la 2ème loi de Newton, donner l'expression du vecteur $\vec T $ .
• Construire ce vecteur aux points 4 et 8, en utilisant les vecteurs précédemment tracés. Mesurer les normes des vecteurs .
• Les vecteurs $\vec T $ sont, en théorie, dirigés en tout point vers le point d’attache du pendule. Est-ce le cas ici ? Sinon, proposer des raisons expliquant les écarts constatés.
• Expliquer comment la deuxième loi de Newton peut être utilisée pour relier le vecteur et les forces appliquées sur un système.
EXERCICES : 11, 14, 18, 20, 22, 29 et 31 P 279 à 283.
COURS
C1. Centre de masse d'un système.
C11. Définition.
Le centre de masse G d'un système quelconque est le point situé à la position moyenne de la masse de ce système.
On l'appelle aussi centre de gravité ou centre d'inertie.
C12. Position du centre de masse.
|
Dans un champ de gravité uniforme, le centre de masse se situe au centre de gravité, généralement noté G. C'est le barycentre des masses. Dans le cas d'un système homogène, il se situe au centre géométrique du système. Dans le cas d'un système non homogène, il se trouve du côté où le système est plus massique. |
|
Détermination de sa position. On peut déterminer expérimentalement sa position de différentes façons, il se trouve :
C'est le point du système qui a un mouvement particulier lorsque le système est en mouvement. |
 |
C13. Propriété du centre de masse.
Le centre de masse d'un système est celui qui a la trajectoire la plus simple lorsque ce système est en mouvement.
Dans le cas du marteau lancé dans le laboratoire, le centre de gravité se déplace selon une parabole, tandis que l'extrémité du manche... ??
On étudiera le mouvement d'un système en considérant que toute la masse est portée en son centre de gravité.
C2. Référentiel galiléen.
C21.Référentiel.
|
Un référentiel est un objet par rapport auquel on étudie le mouvement d'un système. Il est muni d'un repère et d'une échelle de temps.
• Le référentiel terrestre, lié à la Terre est adapté à l'étude du mouvement d'un objet proche de la Terre. • Les référentiels astrocentriques sont liés au centre d'un astre et associés à des axes de directions fixes par rapport à des étoiles lointaines |
 |
C22.Référentiel galiléen.
Un référentiel est dit galiléen si dans ce référentiel, la première loi de Newton (ou principe d'inertie) est vérifiée :
| Il existe une famille de référentiels, appelés galiléens, dans lesquels un point matériel isolé ou pseudo-isolé est au repos ou bien en mouvement rectiligne uniforme. |
NB : tout référentiel immobile ou en translation rectiligne uniforme par rapport à un référentiel galiléen est donc galiléen.
C23.Exemples.
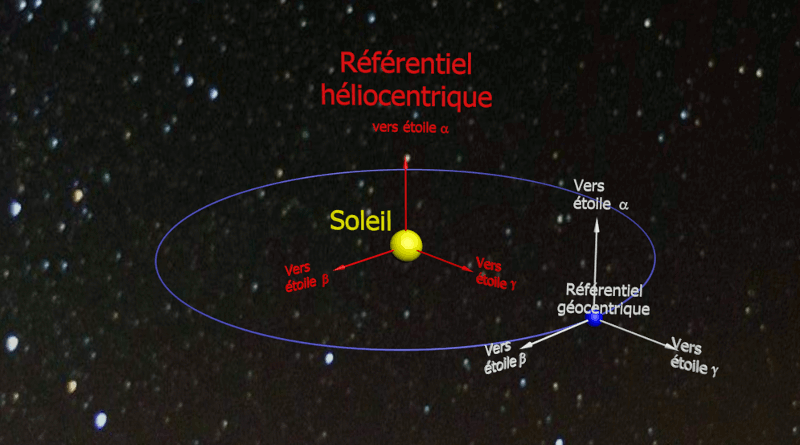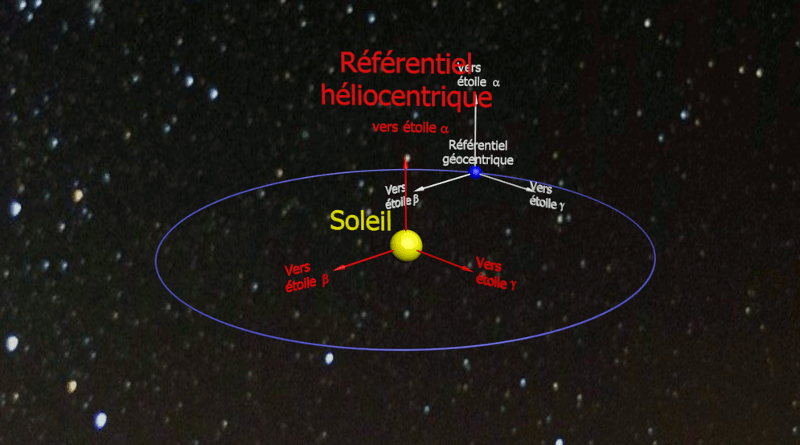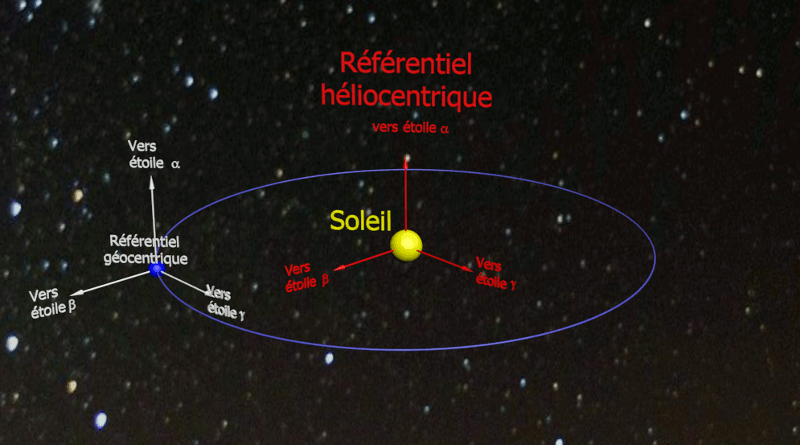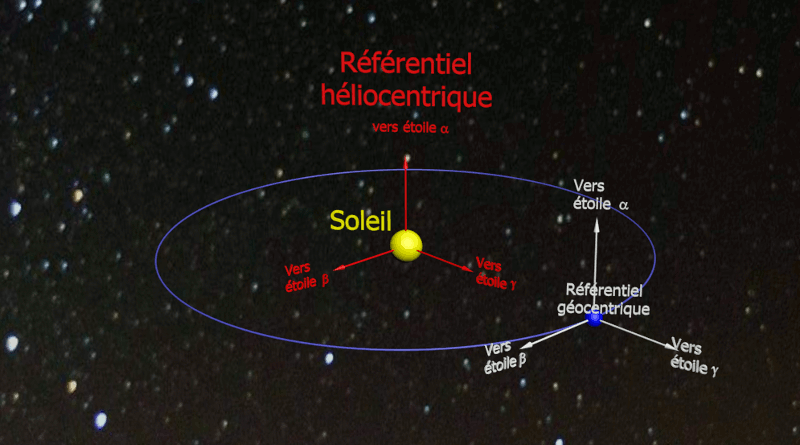
Le référentiel héliocentrique (repère situé au centre du Soleil) muni de trois axes dirigés vers des étoiles est considéré comme galiléen.
Le référentiel géocentrique (repère situé au centre de la Terre) muni de trois axes dirigés vers des étoiles pourra être considéré comme galiléen sin on étudie le mouvement d'un système n'excédant pas quelques heures.
Le référentiel terrestre (repère situé à la surface de la Terre) muni de trois axes dirigés vers des étoiles pourra être considéré comme galiléen sin on étudie le mouvement d'un système n'excédant pas quelques minutes.
C24.Référentiel non galiléen.
|
Inversement, si un système au repos est soumis à des actions mécaniques qui ne se compensent pas dans un référentiel, alors le principe d'inertie ne s'applique pas et le référentiel n'est pas galiléen.
Tout référentiel en mouvement de translation accéléré ou ralenti, ou en rotation par rapport à un référentiel galiléen n'est pas galiléen.
Dans l'exemple ci-contre, le référentiel lié à une cabine n'est pas galiléen, contrairement à celui lié au manège. |
 |
C3. Deuxième loi de Newton.
C31.Enoncé.
|
 |
C32.Equilibre d'un système.
|
Un système à l'équilibre dans un référentiel galiléen est en équilibre si et seulement si les vecteurs vitesse et accélération sont nuls :
$\vec v = \vec 0\;\; et\;\; \vec a = \vec 0 $
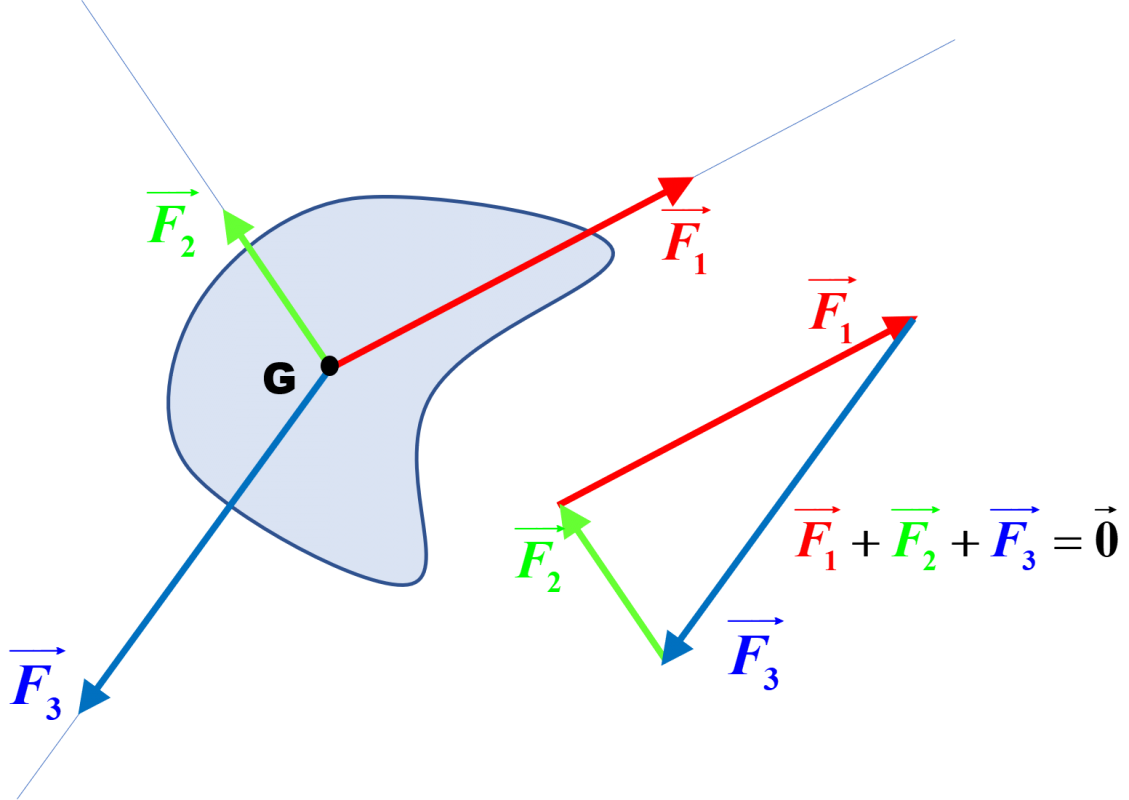
Il en résulte que la somme des forces appliquées à ce système est nulle :
$\sum {\overrightarrow {F_{ext}}} = \vec 0 $
NB : ce n'est pas parce-que la somme des "vecteurs force" se compense que le système est immobile. |
 |
C33. Des forces à l'accélération... et même au-delà !!
|
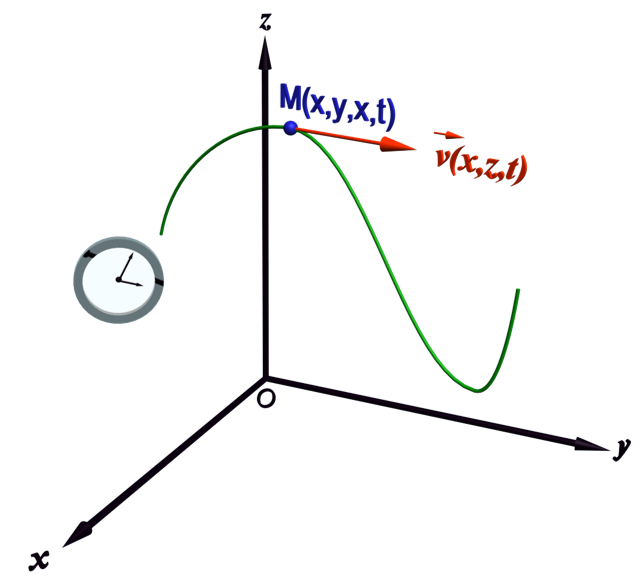
• En appliquant la deuxième loi de Newton : $\sum {\overrightarrow {F_{ext}}} = m.\overrightarrow {a_{G}} $ , on pourra ainsi déterminer le vecteur accélération du système et ses composantes dans le référentiel choisi. |
 |
|
• En "intégrant" par rapport au temps, on pourra ainsi accéder aux composantes temporelles de son vecteur vitesse, en prenant en compte les composantes initiales de la vitesse $ \left ( \vec {a(t)} = \dfrac {d \overrightarrow {v(t)}} {dt} \right ) $.
|
 |
|
• En "intégrant" par rapport au temps une nouvelle fois, on pourra ainsi accéder aux composantes temporelles de sa position $ \left ( \vec {v(t)} = \dfrac {d \overrightarrow {OG(t)}} {dt} \right ) $.
• Pour finir, un lien entre ces composantes temporelles permettra donc d'accéder à l'équation spatiale de sa trajectoire dans le référentiel choisi. |
 |
Commentaires
-

- 1. ghomari Le 30/01/2023
comment puis-je telecharger les differents logiciels-

- bob_coyoteLe 01/02/2023
Bonjour. J'ai mis des liens, au-dessous de chacun d'eux.
-

- 2. ghomari Le 30/01/2023
comment puis-je telecharger les differents logiciels
Ajouter un commentaire