La Lunette Astronomique
ACTIVITES
A1 : Réalisation d'une lunette astronomique.
|
Depuis le XVIIe siècle sont apparues, les lunettes astronomiques se sont perfectionnées mais comportent toujours au moins deux lentilles convergentes.
Objectif : réaliser étudier un modèle de lunette astronomique. |
 |
|
|
|
|
Réaliser.
• Calculer les distances focales $f'_0$, $f'_1$, $f'_2$, et $f'_3$ des lentilles utilisées.
S'approprier :
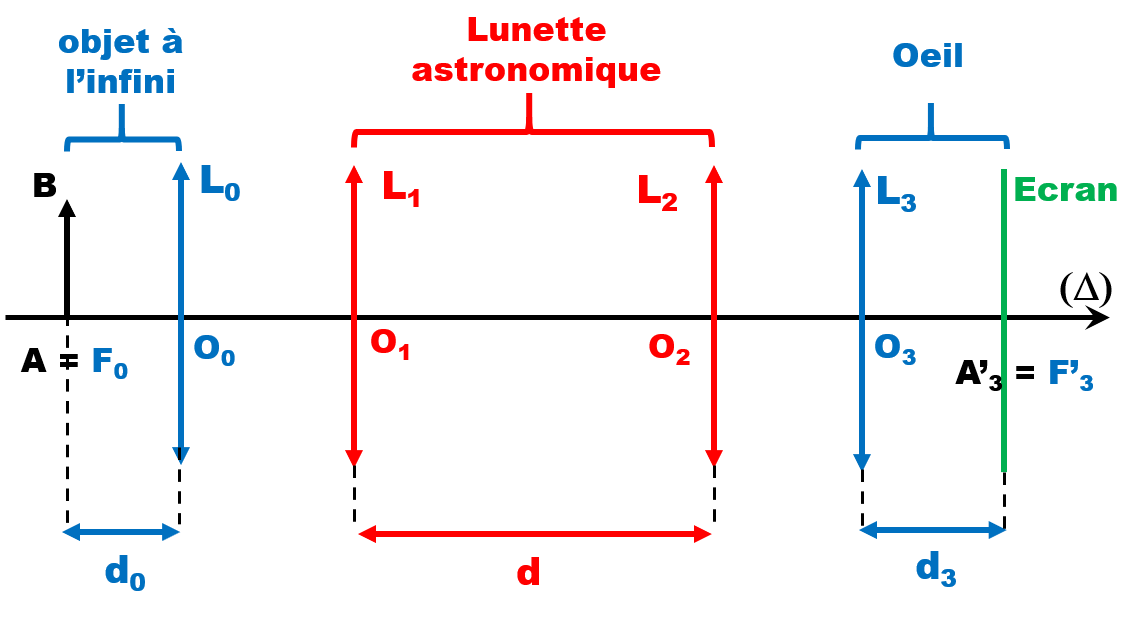
• Lire les protocoles 1 et 2 et préciser les expressions et valeurs des distances $f'_0$, $d$ et $d_3$ matérialisées sur le schéma du doc4.
Réaliser.
• Réaliser sur le banc optique les montages du protocole un point adapter si nécessaire la distance entre $f'_0$ et l'écran pour que l'image soit bien nette.
• Mesurer sur l'écran la taille de l'image définitive obtenue. L'image est-elle dans le même sens que l'objet ou renversée par rapport à l'objet ?
Analyser - Raisonner :
• Ajouter la maquette de lunette astronomique (protocole 2). Ajuster si nécessaire la position de la lentille $f'_0$ pour que l'image soit nette.
• Noter la position de $A_1B_1$ et calculer les didtances $O_1A_1$ et $A_1O_2$. Commenter.
• Mesurer sur l’écran la taille de l’image. Quelle est son orientation ?
• Le grossissement $G$ de la lunette peut ici être calculé comme un quotient. Lequel ? faire le calcul.
Réaliser.
• Calculer $G \ = \ \dfrac{C_2}{C_1}$ avec son expression théorique . Comparer les deux valeurs.
• Retirer l’objet et l’œil simulés, et observer à l’aide de la lunette un objet éloigné. Décrire les observations.
• Réaliser les deux schémas des deux situations étudiées ici, à une échelle que l’on précisera :
- Schéma sans la lunette ;
- Schéma avec la lunette ;
On tracera le trajet de trois rayons issus de B à travers les lentilles.
A2. Lunettes astronomiques commerciales.
Depuis l’invention, au début du XVIIe siècle, de la lunette astronomique par Johannes Kepler, les astronomes amateurs et professionnels ont utilisé cet instrument pour observer le ciel.
Objectif : Exploiter les données caractéristiques d’une lunette commerciale.
|
Doc 1 : Extraits des caractéristiques de deux lunettes.
|
|
|
Doc 3 : Cercle oculaire. Pour observer à travers une lunette, l’œil doit être placé sur le cercle oculaire, qui est l’image de l’objectif par l’oculaire. A cet endroit, le faisceau lumineux sortant de la lunette est le plus étroit.
|
S'approprier :
• Pour les deux lunettes du document 1, déterminer les valeurs des grossissements possibles avec les oculaires fournis.
• Quels grossissements obtiendrait-on en adaptant les oculaires du document 2 à la lunette du modèle 2 ?
• Les oculaires du document 2 sont adaptables sur la monture du modèle 2 mais ont des hauteurs différentes.
• Expliquer pourquoi, en utilisant le caractère afocal de la lunette astronomique.
Analyser-raisonner
• Monter que le diamètre du cercle oculaire (document 3) est égal au diamètre de l’objectif divisé par le grossissement de la lunette.
• Estimer le diamètre de la pupille d’un œil.
• Pour une bonne observation, le diamètre du cercle oculaire doit être inférieur au diamètre de la pupille de l’œil. Pourquoi ? Est-ce le cas pour les deux lunettes du doc.1 avec tous les oculaires fournis ?
Communiquer
• Le grossissement de la lunette est un paramètre important. Expliquer pourquoi, d’après les prix des deux lunettes présentes, ce n’est pas certainement pas le seul.
• Le diamètre de l’objectif est une donnée cruciale. Pour une même distance focale, vaut-il mieux un diamètre élevé ou faible ? Pourquoi ? En quoi cela limite-t-il le grossissement ?
EXERCICES : 13 ; 14 ; 16 ; 19 ; 24 ; 29 ; 30 ; 34 ; 37 P465 à 471
COURS
C0. Rappels.
C01. Caractéristiques.
• Une lentille convergente est un objet transparent de symétrie sphérique capable de réfracter la lumière.
• Une lentille convergente est caractérisée par sa distance focale $f$. Cette grandeur s’exprime en mètres.
NB :
1. dans les métiers de l’optique, on utilise plutôt la vergence C, inverse de la distance focale :
$C=\dfrac {1}{f'} $
Cette grandeur s’exprime en dioptrie de symbole δ (équivalent au m-1).
2. Cette distance focale peut être déterminée simplement : c’est la distance entre la lentille et le point de convergence de tous les rayons provenant de l’infini.
• L’axe de symétrie d’une lentille est appelé axe optique. Il est orienté dans le sens de propagation de la lumière.
• Le centre de symétrie O de la lentille est appelé centre optique. Il se trouve sur l’axe optique.
• Le foyer image F’ est le point de l’axe optique situé à une distance f’ après O.
• Le foyer objet F est le point de l’axe optique situé à une distance f’ avant O.
$\color{red}{OF=OF'=f'=\dfrac {1}{C} >0}$
C02 Construction graphique.
• Tout rayon qui passe par le centre optique O n’est pas dévié.
• Tout rayon qui passe par le foyer objet F émerge parallèlement à l’axe optique.
• Tout rayon parallèle à l’axe optique émerge en passant par F’.
Un objet est représenté par une flèche verticale AB, perpendiculaire à l’axe optique (A est sur l’axe optique).
Son image A’B’ est aussi perpendiculaire à l’axe optique.
Tous les rayons passant par B se croisent en B’.
Il suffit donc de tracer deux des trois rayons particuliers définis précédemment pour déterminer sa position.
A’ est sur l’axe optique.
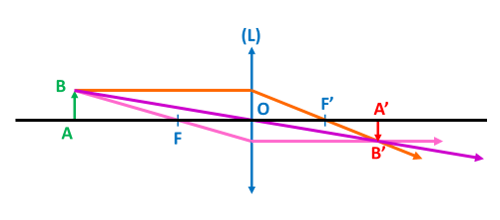
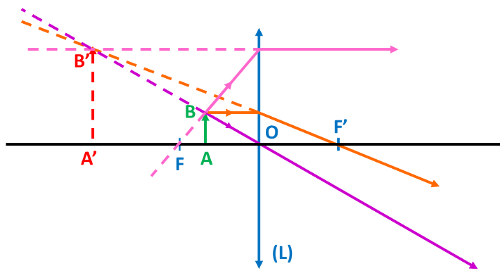
C03 Image réelle ou virtuelle.
• L’image réelle est observable sur un écran au croisement des rayons émergeant de la lentille.
• L’image virtuelle ne peut être observée sur un écran. Elle se trouve avant la lentille, du même côté de l’objet. On l’observe en se plaçant après la lentille.
 |
 |
C04. Relation de conjugaison.
Pour mesurer les positions des points images et objets, on doit définir un repère :
- Son origine est le centre optique O de la lentille.
- L’axe des abscisses (Ox) est l’axe optique de la lentille, orienté dans le sens de propagation de la lentille.
- L’axe des ordonnées (Oy) est perpendiculaire à l'axe des abscisses.
On peut prévoir la position de l’image A’, en connaissant la position de l’objet A et la distance focale f’ de la lentille.
|
$\color{red}{\dfrac {1}{\overline {OA'}} - \dfrac {1}{\overline {OA}} = \dfrac {1}{f'}}$ |
$\overline {OA}, \overline {OA'}, \ et \ f' \ en \ mètres \ (m) $ |
C05. Grandissement.
Le grandissement caractérise l’aspect de l’image obtenue par rapport à l’objet.
Il est défini par :
$\color{red}{\gamma = \dfrac {1}{\overline {A'B'}} = \dfrac {\overline {OA'}}{\overline {OA}}}$; $\gamma$ n'a pas de dimension.
Sens de l’image :
Le signe du grandissement $\gamma$ indique le sens de l’image par rapport à celui de l’objet.
- Si $\gamma \ > \ 0$ , l’image et l’objet sont dans le même sens, on dit que l’image est droite.
- Si $\gamma \ < \ 0$ , l’image et l’objet n’ont pas le même sens, on dit que l’image est renversée.
Taille de l’image :
La valeur du grandissement $\gamma$ permet de déterminer la taille de l’image par rapport à celle de l’objet.
- Si $\left | \gamma \right | $ , l’image est plus grande que l’objet.
- Si $\left | \gamma \right | $ , l’image est plus petite que l’objet.
C1. La lunette astronomique.
C11. Constitution.
|
La lunette astronomique est constituée : - D'un objectif. - D'un oculaire.
|
 |
Schéma :
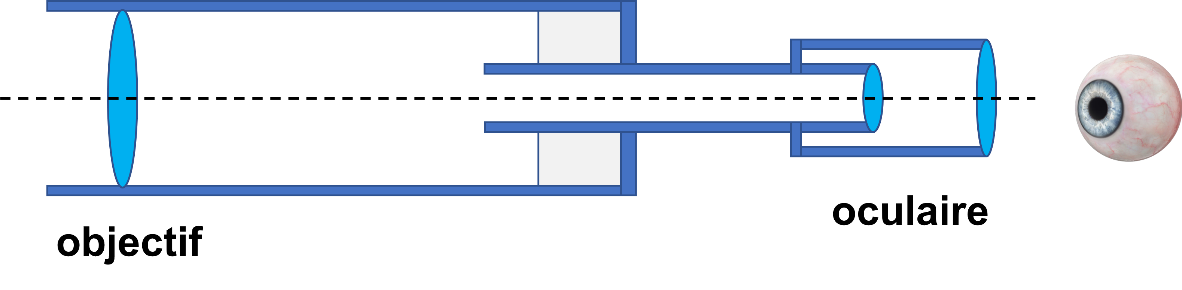
C12. Modélisation.
La lunette étant afocale, le foyer principal image de l'objectif correspond avec le foyer principal objet de l'oculaire.
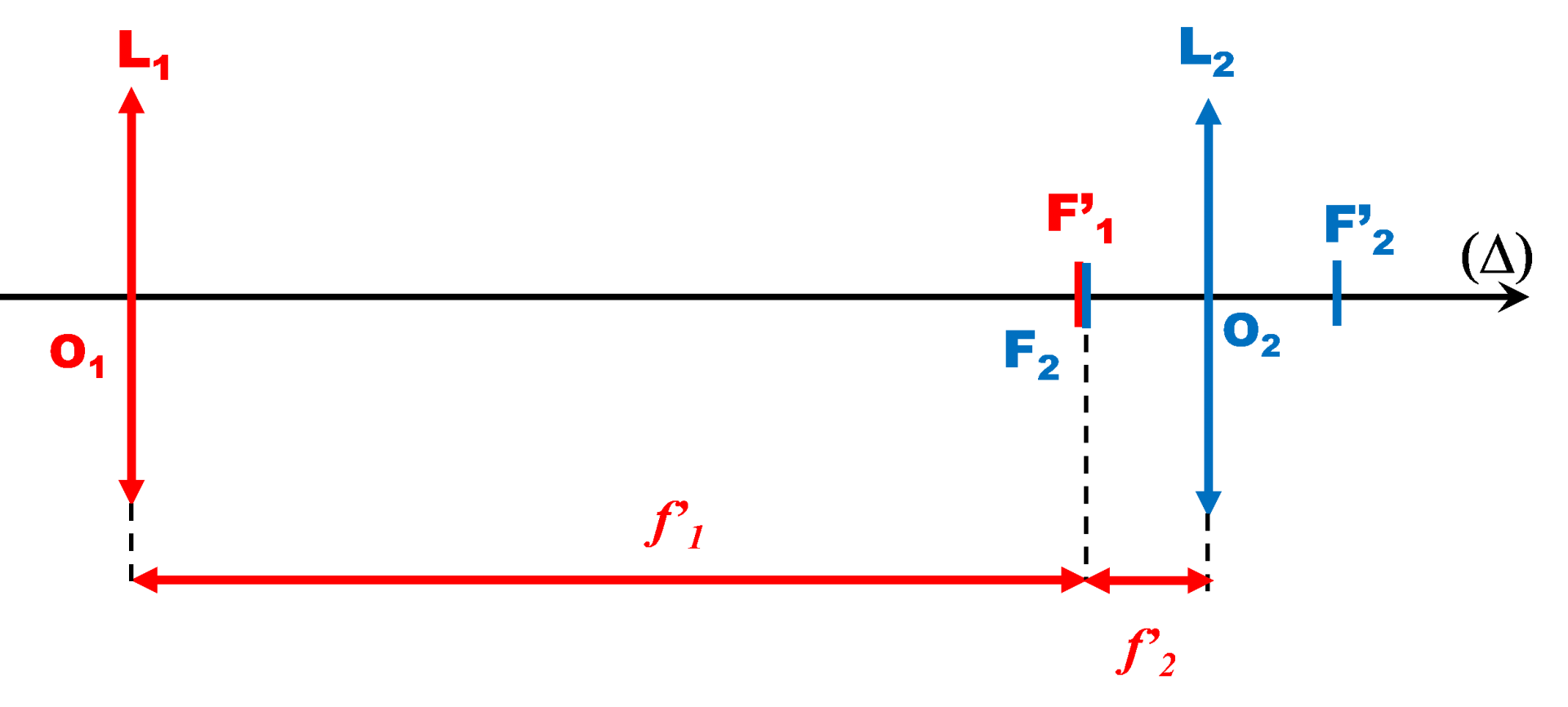
L'objectif de grande distance focale donne de l'objet situé à l'infini une image intermédiaire située dans son plan focal image.
Cette image intermédiaire placée dans le plan focal objet de l'oculaire, renvoie une l'image observée à l'infini.
C2. Formation des images.
C21. Construction graphique.
C21a. Image intermédiaire.
L'astre observé est l'objet AB situé à l'infini.
Le point A, situé sur l'axe optique et les rayons provenant de B pénètrent par l'objectif selon un angle $\theta$ par rapport à l'axe optique.
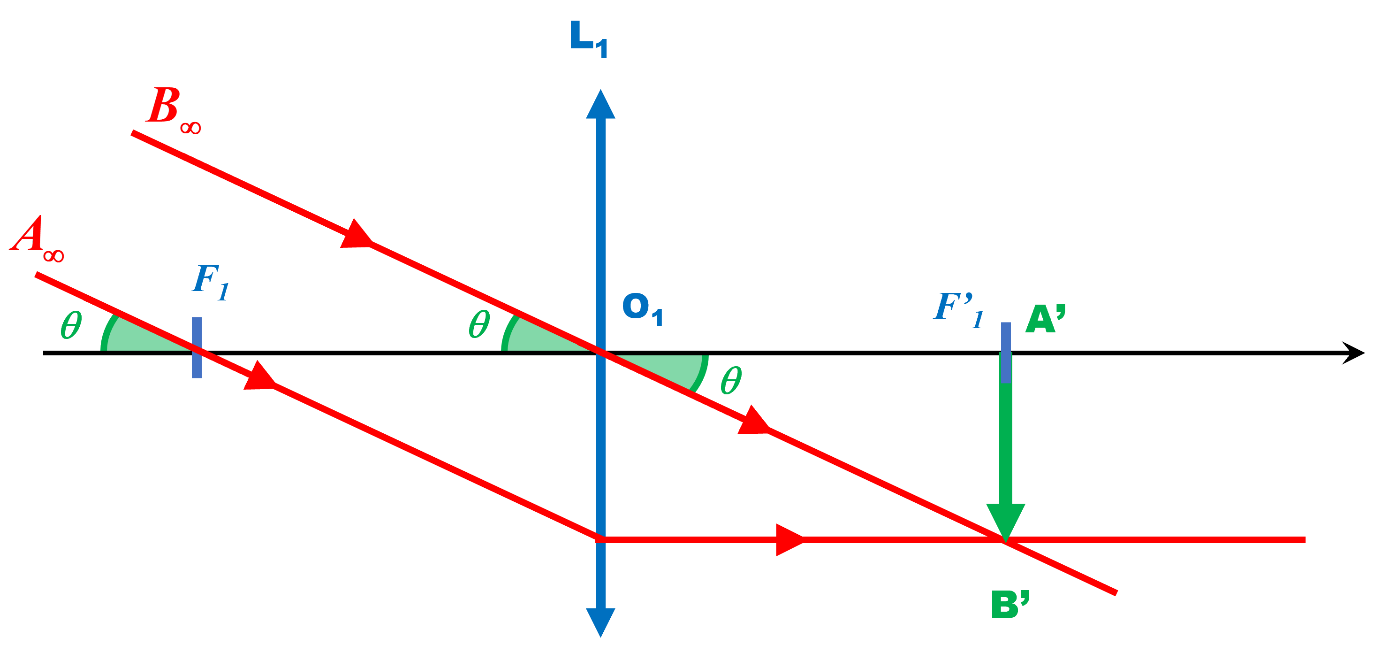
Le rayon provenant de $B$ situé à l'infini et passant par le centre optique $O_1$ de l'objectif n'est pas dévié.
Le rayon provenant de $A$ situé à l'infini et passant par le foyer objet $F_1$ de l'objectif ressort de la lentille parallèlement à son axe optique.
Les deux rayons se croisent en $B'$, image de $B$ dans le plan focal image de l'objectif.
C21b. Image donnée par l'oculaire.
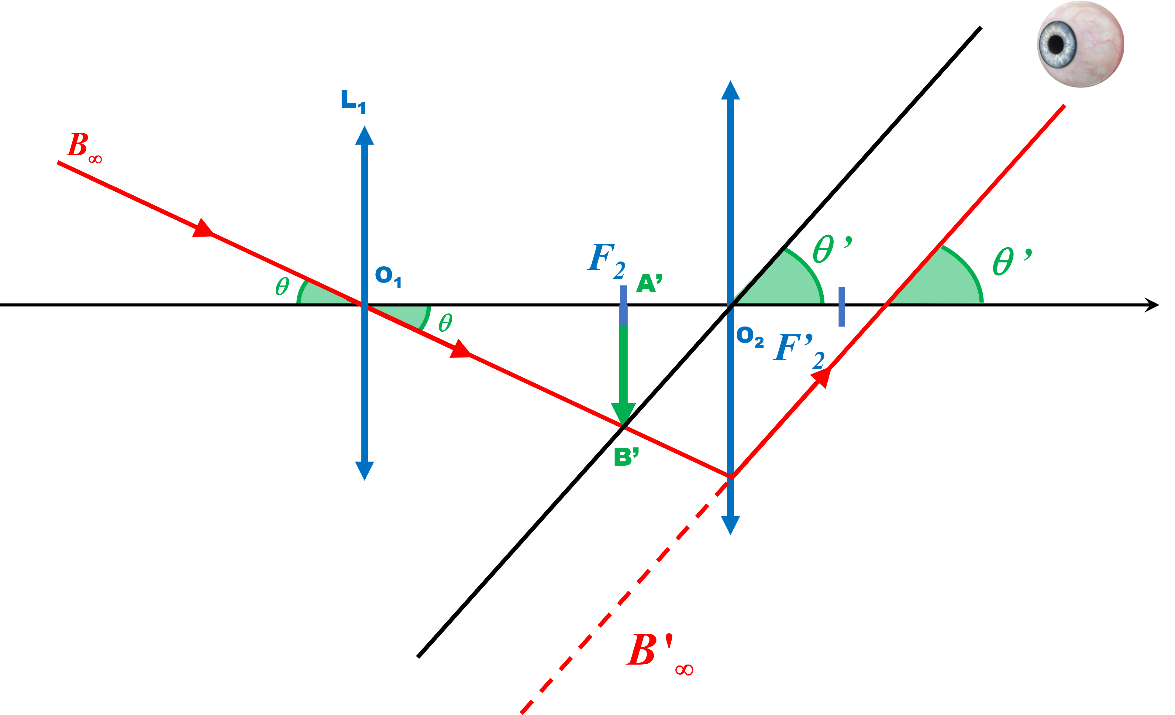
L'image intermédiaire $A'B'$ étant dans le plan focal de l'oculaire, son image sera située à l'infini.
Le rayon passant par $B'$ et $O_2$ n'est pas dévié.
Tous les rayons lumineux émergents ressortent parallèlement à ce rayon selon une direction $\theta '$ par rapport à l'axe optique.
L'astre observé est l'objet AB situé à l'infini.
Le point A, situé sur l'axe optique et les rayons provenant de B pénètrent par l'objectif selon un angle $\theta$ par rapport à l'axe optique.

Le rayon provenant de $B$ situé à l'infini et passant par le centre optique $O_1$ de l'objectif n'est pas dévié.
Le rayon provenant de $A$ situé à l'infini et passant par le foyer objet $F_1$ de l'objectif ressort de la lentille parallèlement à son axe optique.
Les deux rayons se croisent en $B'$, image de $B$ dans le plan focal image de l'objectif.
C21b. Image donnée par l'oculaire.

L'image intermédiaire $A'B'$ étant dans le plan focal de l'oculaire, son image sera située à l'infini.
Le rayon passant par $B'$ et $O_2$ n'est pas dévié.
Tous les rayons lumineux émergents ressortent parallèlement à ce rayon selon une direction $\theta '$ par rapport à l'axe optique.
la
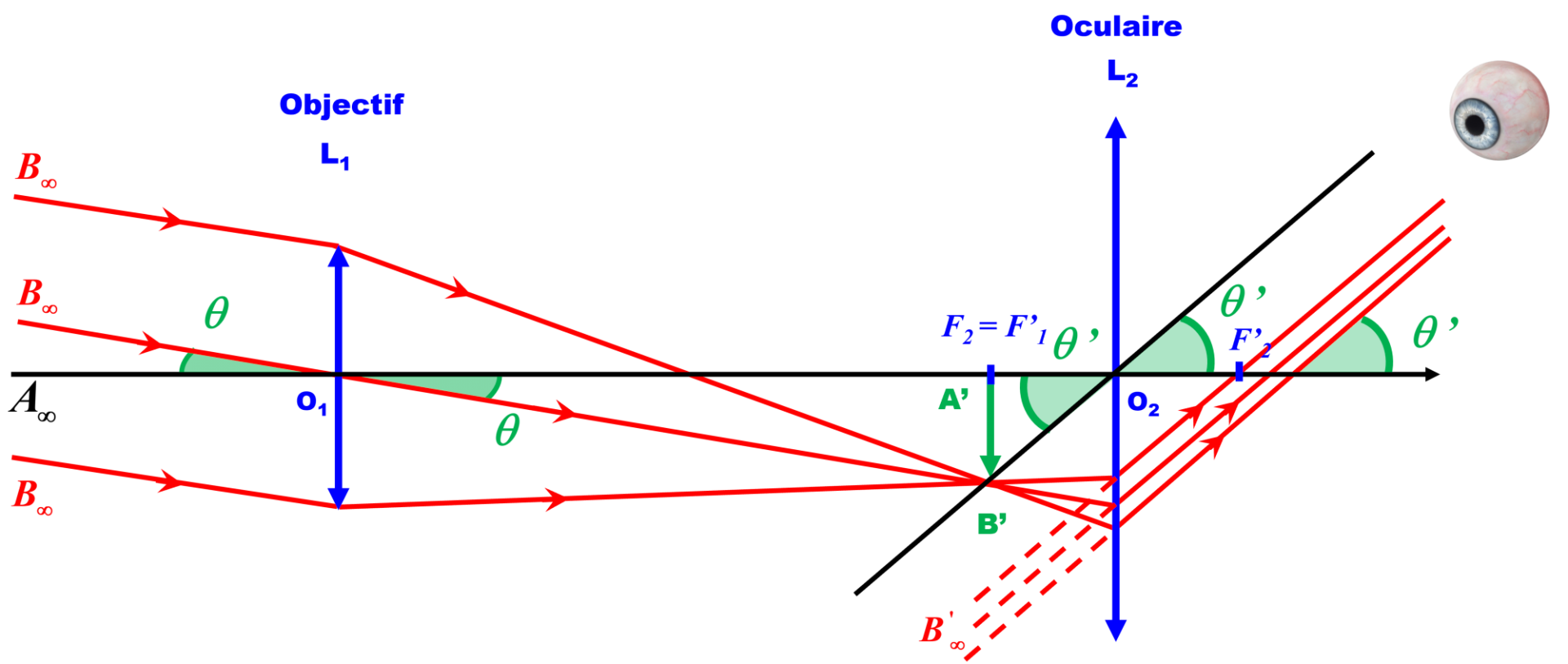
C21c. Construction finale.
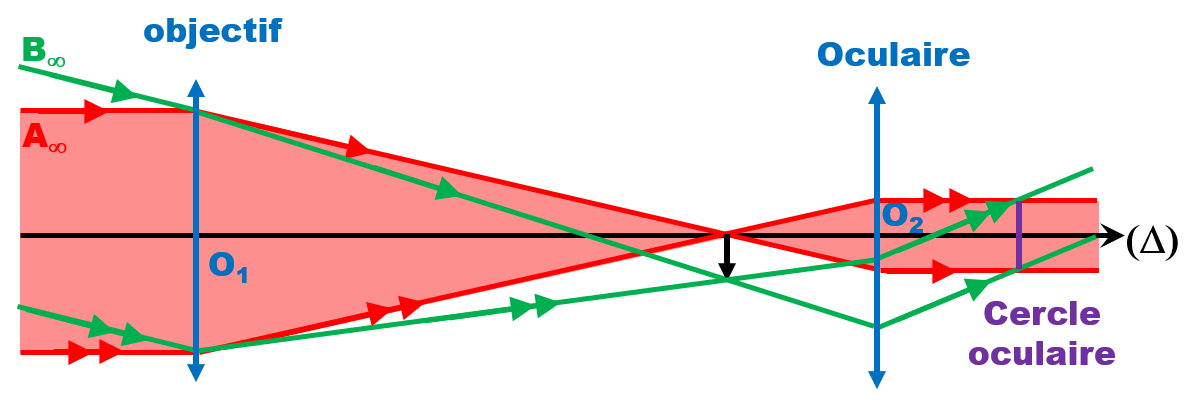
Marche de trois rayons à travers la lunette afocale.
C22. Relations de conjugaisons.
C22a. A l'objectif.
$\dfrac{1}{\overline{O_1A^ \prime}} \ - \ \dfrac{1}{\overline{O_1A}} \ = \ \dfrac{1}{f_1} \ \ \ \ \Leftrightarrow \ \ \ \ \dfrac{1}{\overline{O_1A^ \prime}} \ = \ \dfrac{1}{f_1} \ + \ \dfrac{1}{\overline{O_1A}}$
L'objet étant à l'infini, on a : $\dfrac{1}{\overline{OA^ \prime }} \ = \ \dfrac{1}{f_1}$ soit : $\overline{OA^ \prime} \ = \ {f_1} \ = \ \overline{O_1F_1^ \prime}$
C22b. A l'oculaire.
$\dfrac{1}{\overline{O_2A_{finale}}} \ - \ \dfrac{1}{\overline{O_2A^ \prime}} \ = \ \dfrac{1}{f_2} \ \ \ \ \Leftrightarrow \ \ \ \ \dfrac{1}{\overline{O_2A_{finale}}} \ = \ \dfrac{1}{f_2} \ + \ \dfrac{1}{\overline{O_2A^{ \prime}}}$
L'objet étant à l'infini, on a : $\overline{O_2A_{finale}} \ = \ -f_2^ \prime \ = \ - \overline{O_2F_2^ \prime} \ = \ \overline{O_2F_2}$
C23. Conclusion.
Le point $A^{ \prime}<$ style="font-family:arial black ; color:red; font-size:24px;">C2. Formation des images.
C21. Construction graphique.
C21a. Image intermédiaire.
L'astre observé est l'objet AB situé à l'infini.
Le point A, situé sur l'axe optique et les rayons provenant de B pénètrent par l'objectif selon un angle $\theta$ par rapport à l'axe optique.

Le rayon provenant de $B$ situé à l'infini et passant par le centre optique $O_1$ de l'objectif n'est pas dévié.
Le rayon provenant de $A$ situé à l'infini et passant par le foyer objet $F_1$ de l'objectif ressort de la lentille parallèlement à son axe optique.
Les deux rayons se croisent en $B'$, image de $B$ dans le plan focal image de l'objectif.
C21b. Image donnée par l'oculaire.

L'image intermédiaire $A'B'$ étant dans le plan focal de l'oculaire, son image sera située à l'infini.
Le rayon passant par $B'$ et $O_2$ n'est pas dévié.
Tous les rayons lumineux émergents ressortent parallèlement à ce rayon selon une direction $\theta '$ par rapport à l'axe optique.
L'astre observé est l'objet AB situé à l'infini.
Le point A, situé sur l'axe optique et les rayons provenant de B pénètrent par l'objectif selon un angle $\theta$ par rapport à l'axe optique.

Le rayon provenant de $B$ situé à l'infini et passant par le centre optique $O_1$ de l'objectif n'est pas dévié.
Le rayon provenant de $A$ situé à l'infini et passant par le foyer objet $F_1$ de l'objectif ressort de la lentille parallèlement à son axe optique.
Les deux rayons se croisent en $B'$, image de $B$ dans le plan focal image de l'objectif.
C21b. Image donnée par l'oculaire.

L'image intermédiaire $A'B'$ étant dans le plan focal de l'oculaire, son image sera située à l'infini.
Le rayon passant par $B'$ et $O_2$ n'est pas dévié.
Tous les rayons lumineux émergents ressortent parallèlement à ce rayon selon une direction $\theta '$ par rapport à l'axe optique.
la
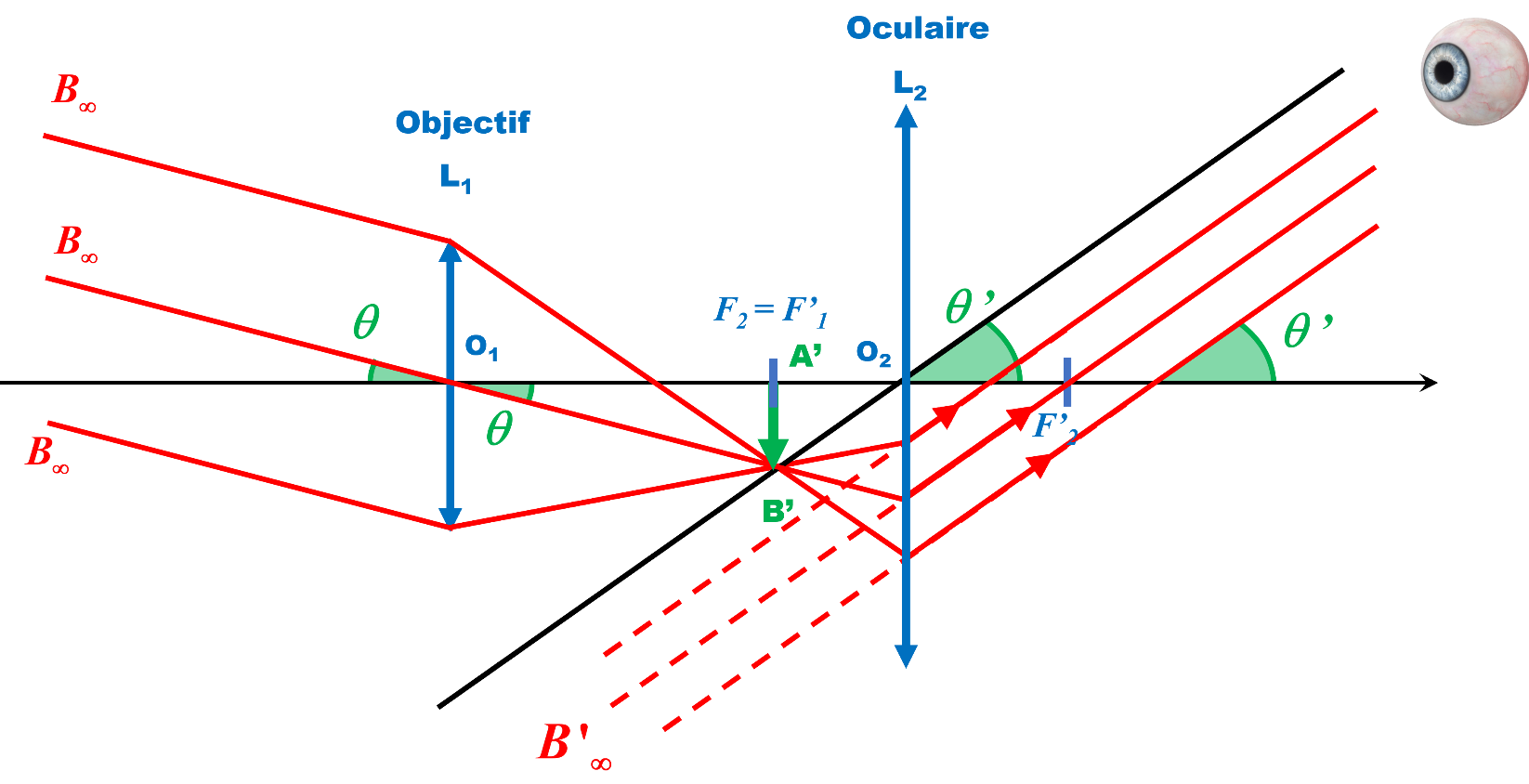
C21c. Construction finale.
Marche de trois rayons à travers la lunette afocale.
C22. Relations de conjugaisons.
C22a. A l'objectif.
$\dfrac{1}{\overline{O_1A^ \prime}} \ - \ \dfrac{1}{\overline{O_1A}} \ = \ \dfrac{1}{f_1} \ \ \ \ \Leftrightarrow \ \ \ \ \dfrac{1}{\overline{O_1A^ \prime}} \ = \ \dfrac{1}{f_1} \ + \ \dfrac{1}{\overline{O_1A}}$
L'objet étant à l'infini, on a : $\dfrac{1}{\overline{OA^ \prime }} \ = \ \dfrac{1}{f_1}$ soit : $\overline{OA^ \prime} \ = \ {f_1} \ = \ \overline{O_1F_1^ \prime}$
C22b. A l'oculaire.
$\dfrac{1}{\overline{O_2A_{finale}}} \ - \ \dfrac{1}{\overline{O_2A^ \prime}} \ = \ \dfrac{1}{f_2} \ \ \ \ \Leftrightarrow \ \ \ \ \dfrac{1}{\overline{O_2A_{finale}}} \ = \ \dfrac{1}{f_2} \ + \ \dfrac{1}{\overline{O_2A^{ \prime}}}$
L'objet étant à l'infini, on a : $\overline{O_2A_{finale}} \ = \ -f_2^ \prime \ = \ - \overline{O_2F_2^ \prime} \ = \ \overline{O_2F_2}$
C23. Conclusion.
Le point $A^{ \prime}$, image du point$A$ est donc confondu avec le foyer objet de l'oculaire.
L'image intermédiaire $A^{ \prime}B^{ \prime} $est située dans le plan focal image de l'objectif ET dans le plan focal objet de l'oculaire.
L'image intermédiaire $A^{ \prime}B^{ \prime} $est située dans le plan focal image de l'objectif ET dans le plan focal objet de l'oculaire.
C3. Caractéristiques de la lunette..
C31. Grossissement.
A travers la lunette, on voit l'astre comme s'il était situé à une distance plus petite que la distance réelle à laquelle il se situe réellement.
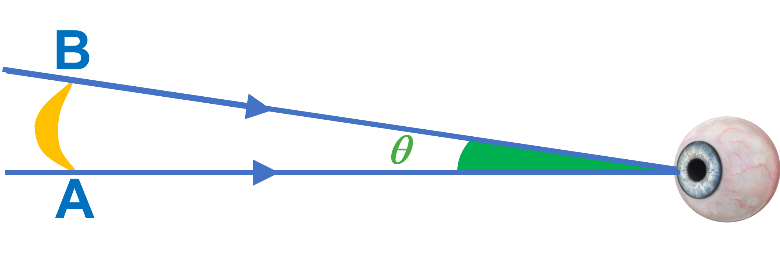
L'angle $\theta$ sous lequel l'astre est vu depuis le lieu d'observation est appelé DIAMETRE APPARENT.
|
Diamètre apparent d'un objet observé à l'œil nu.
|
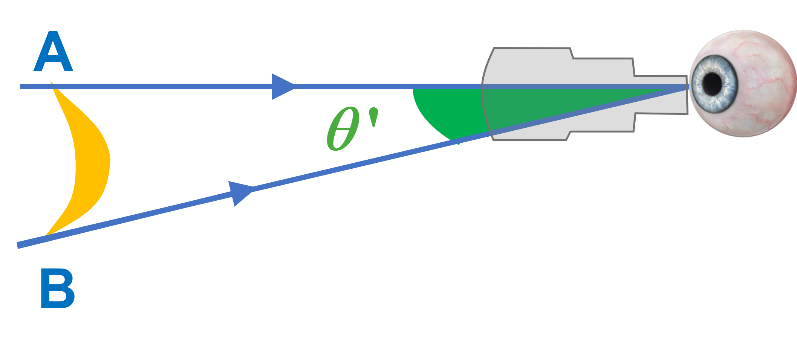
Image virtuelle, renversée et grossie vue à travers la lunette.
|
Le grossissement $\overline{G}$ de la lunette est défini selon : $\overline{G} \ = \ \dfrac{\theta \prime}{\theta}$
Dans le cas de la lunette afocale, $F_1^ \prime$, $F_2$ et $A^ \prime$ sont confondus.

Dans les triangles $O_1A^ \prime B^ \prime$ et $O_2B^ \prime A^ \prime$, rectangles en $A^ \prime$, on peut donc écrire :
$tan \theta \ = \ \theta \ = \dfrac{\overline{A^ \prime B^ \prime}}{\overline{O_1A^ \prime}} \ = \ \dfrac{\overline{A^ \prime B^ \prime}}{f_1}$ et : $tan \theta^ \prime \ = \ \theta^ \prime \ = \dfrac{\overline{A^ \prime B^ \prime}}{\overline{O_2A^ \prime}} \ = \ \dfrac{\overline{A^ \prime B^ \prime}}{-f_2}$
Soit :
$\dfrac{\theta^ \prime}{\theta} \ = \ \dfrac{\dfrac{\overline{A^ \prime B^ \prime}}{-f_2}}{\dfrac{\overline{A^ \prime B^ \prime}}{f_1}} \ = \ \dfrac{f_1}{-f_2} $
Le grossissement (sans unité) est donc : $\overline G \ = \ \dfrac{\theta^ \prime}{\theta} \ = \ = \ \dfrac{f_1}{-f_2}$
Remarque :
Cette valeur est négative.
Pour que le grossissement soit le plus grand possible, il faudra que le rapport $\dfrac{f_1}{f_2}$ soit supérieur à 1 est donc que la distance focale de l'objectif soit supérieure à celui de l'oculaire.
C32. Diamètre de l'objectif.
Les faisceaux lumineux qui entrent dans la lunette sont limités par la monture de l'objectif.
Le cercle oculaire de la lunette correspond à l'image donnée par l'oculaire de la monture.
C'est à cet endroit qu'il faut placer l'œil pour recevoir un maximum de lumière.
Plus le diamètre de l'objectif sera grand, plus la quantité de lumière sera grande.
NB : pour l'observation du Soleil, on diminue ce diamètre en plaçant un obturateur permettant de limiter cette quantité de lumière évitant ainsi de détériorer le matériel d'observation qui ne sera pas l'œil.
Ajouter un commentaire