Action mécanique sur un système

ACTIVITES

A1. Modéliser une action par une force.

Ginette et le clou.

Doc 1 :Situation.

Ginette l'araignée aperçoit un clou et un aimant posés sur une table.

Elle s'approche, suspendue à son fil en soie pour observer plus près.

Gérard regarde la scène et vient y mettre son grain de sel.

Doc 2 :Diagramme objets-interactions.

Lors de l'étude d'un système, celui-ci subit des interactions avec d'autres systèmes extérieurs. Il est utile de construire un diagramme objets-interactions (DOI)

A11. Analyser.

$\bullet$ Définir les différents systèmes de la situation (doc1).

$\bullet$ Représenter le DIO pour chaque système.

A12. Réaliser.

$\bullet$ Représenter, nommer l'(les) action(s) par un vecteur.

$\bullet$ Quels sont les effets de ces actions sur chaque système ?

A2. Archimède.

Doc 1 : Histoire.

La légende veut d'Archimède prit un bain pour réfléchir, et qu'il remarqua que la baignoire débordait quand il entrait.

Il comprit alors que l'immersion d'un corps déplace une quantité d'eau équivalente à son volume. Il se serait alors élancé nu dans la rue en criant : "Eurêka !"

Enoncé :

"Tout corps plongé dans un fluide au repos, entièrement mouillé par celui-ci ou traversant sa surface libre, subit une force verticale, dirigée de bas en haut et égale et opposée au poids du volume de fluide déplacé. Cette force est appelé poussée d'archimède. Elle s'applique au centre de masse du fluide déplacé appeler centre de poussée."

Doc 2 : Modélisation d'une action mécanique par une force.

Une action mécanique exercée sur un système (S) par un système (S') est modélisée par un vecteur $\overrightarrow {F_{S/S'}}$ caractérisé par :

$\bullet$ Son point d'application.

$\bullet$ Sa direction.

$\bullet$ Son sens.

$\bullet$ La valeur de son intensité exprimée en newton (N)

Masse

La Terre exerce sur une masse une force de valeur $P = m \times g$.

m : masse en kg, $g = 10 \ N.kg^{ \ -1}$, P en N.

Doc 3 : "mesurer" une force.

L'intensité de force se mesure en Newton, de symbole N.

Elle se mesure à l'aide d'un dynamomètre.

Doc 4 : Matériel à disposition.

$\bullet$ Une éprouvette graduée.

$\bullet$ Différentes de masses et de volumes différentes.

Archimede

Doc 4 : protocole.

$\bullet$ Pour différentes masses :

$\bullet$ Mesurer la valeur de son poids.

$\bullet$ Introduire la masse dans l'éprouvette.

$\bullet$ Déterminer son volume.

$\bullet$ Mesurer alors la valeur de la force résultante appliquée sur la masse.

$\bullet$ En déduire la valeur de la poussée d'Archimède s'exerçant sur la masse.

$\bullet$ Représenter la situation en faisant apparaître les différentes forces en utilisant une échelle appropriée.

$\bullet$ Compléter le tableau ci-dessous :

masse	$M_1$	$M_2$	$M_3$	$M_4$
$M \ (g)$
$V \ (cm^{ \ 3})$
$P \ (N)$

$\bullet$ Vérifier la relation donnée dans le document 2.

$\bullet$ Mesurer la valeur de la poussée d'Archimède $P_a$ appliquée sur la masse.

masse	$M_1$	$M_2$	$M_3$	$M_4$
$P_a \ (N)$

$\bullet$ Déterminer la masse d'eau déplacée et calculer le poids correspondant. (On rappelle la relation $\rho \ = \ \dfrac{m}{V}$ )

masse	$M_1$	$M_2$	$M_3$	$M_4$
$P_{eau} \ (N)$

$\bullet$ Représenter la situation dans chaque cas.

$M_1$	$M_2$	$M_3$	$M_4$

$\bullet$ Vérifier alors les propos d'Archimède.

A3. La force d'interaction gravitationnelle.

En 1687, Newton élabora une théorie universelle qui permit d'expliquer à la fois le mouvement d'une pomme tombant sur Terre, mais aussi de la Lune autour de la Terre et de toutes les planètes autour du Soleil.

Comment représenter la force gravitationnelle ?

Doc 1 : Textes de Newton.

Proposition VI. théorème VI.

Tous les corps gavitente vers chaque planète, et sur la même planète quelconque leur poids, à égale distance du centre, sont proportionnels à la quantité de matière que chacun d'eux contient.

Proposition LXXVI. Théorème XXXVI.

Deux sphères dont toutes les parties agissent en raison renversée du quarré des distances étant composées l'une et l'autre d'orbes concentriques dont les densités du centre à la circonférence varie suivant une loi quelconque, s'attirent réciproquement avec des forces qui sont en raison renversée du quarré des distances de leurs centres.

Principes mathématiques de la philosophie naturelle, 1726.

Traduction par la comtesse du châtelet.

Doc 2 : Mouvement de la Lune autour de la Terre.

La Lune est un satellite de la Terre qui gravite autour d'elle car la Terre et la Lune exercent mutuellement l'une sur l'autre une attraction gravitationnelle.

Masse de la Terre : $M_T \ = \ 5,98.10^{ \ 24} \ kg$

Masse de la Lune : $M_L \ = \ 7,35.10^{ \ 22} \ kg$

Distance Terre-Lune : $d\ = \ 3,84.10^{ \ 5} \ km$

$\bullet$ Déterminer si la force de gravitation est proportionnelle, inversement proportionnelle ou indépendante des masses de deux systèmes A et B.

$\bullet$ Déterminer si la force de gravitation est proportionnelle, inversement proportionnelle ou indépendante du carré de la distance séparant deux systèmes A et B.

$\bullet$ Déterminer alors l'expression de la force de gravitation :

$\color{black} {\boxed { \ }} \ F_{A/B} \ = \ G \times m_A \times m_B \ \times d^{ \ 2}$	$\color{black} {\boxed { \ }} F_{A/B} \ = \ G \times \dfrac{m_A \times m_B}{d}$
$\color{black} {\boxed { \ }} F_{A/B} \ = \ G \times \dfrac{m_A \times m_B}{d^{ \ 2}}$	$\color{black} {\boxed { \ }} F_{A/B} \ = \ G \times \dfrac{d^{ \ 2}}{m_A \times m_B}$

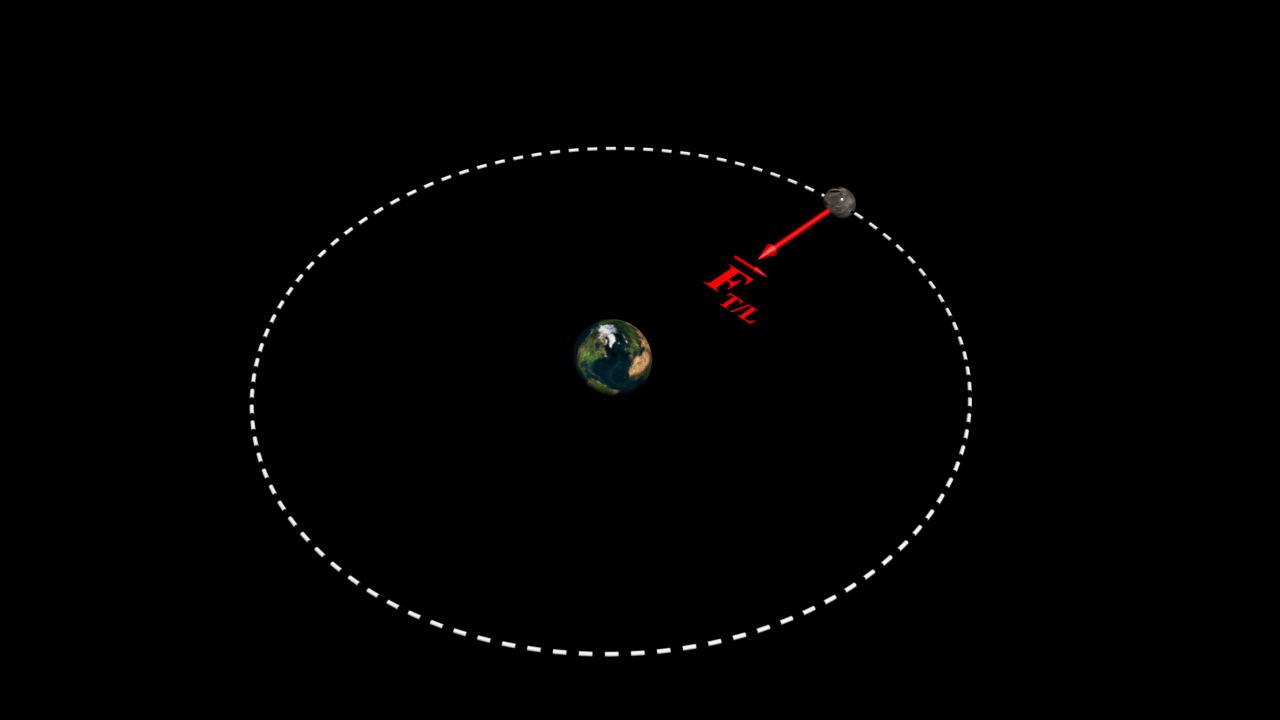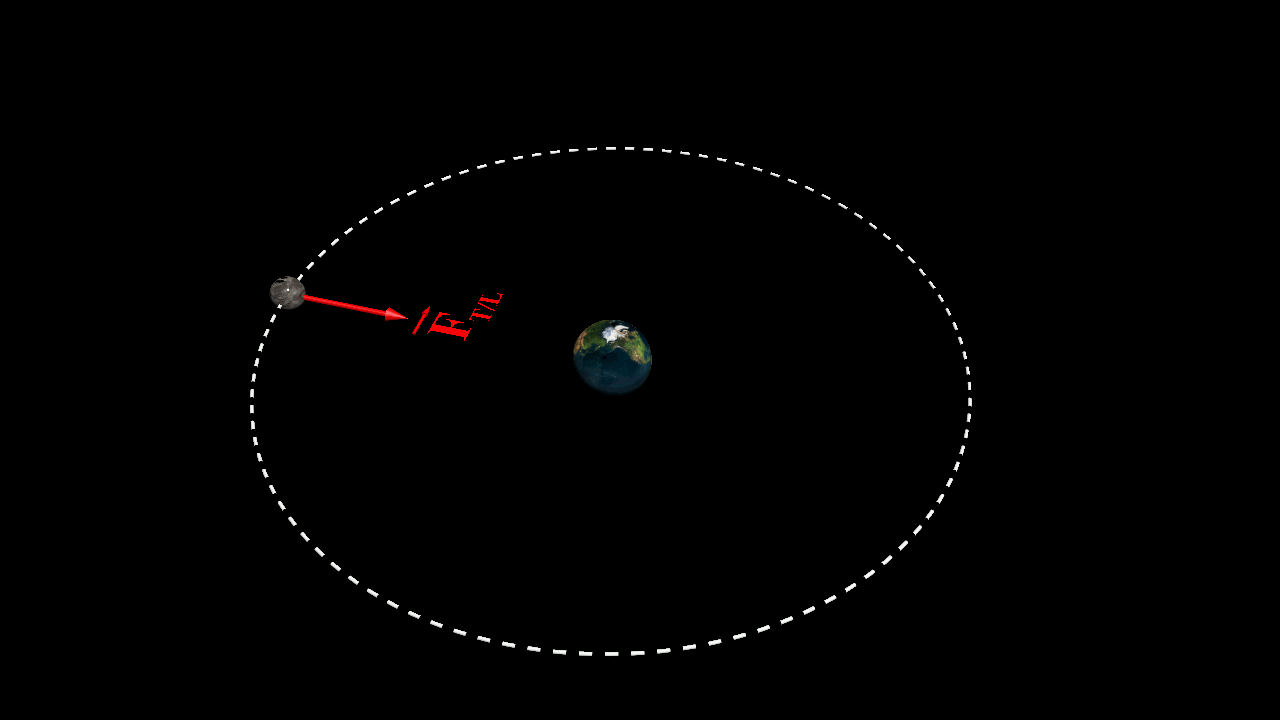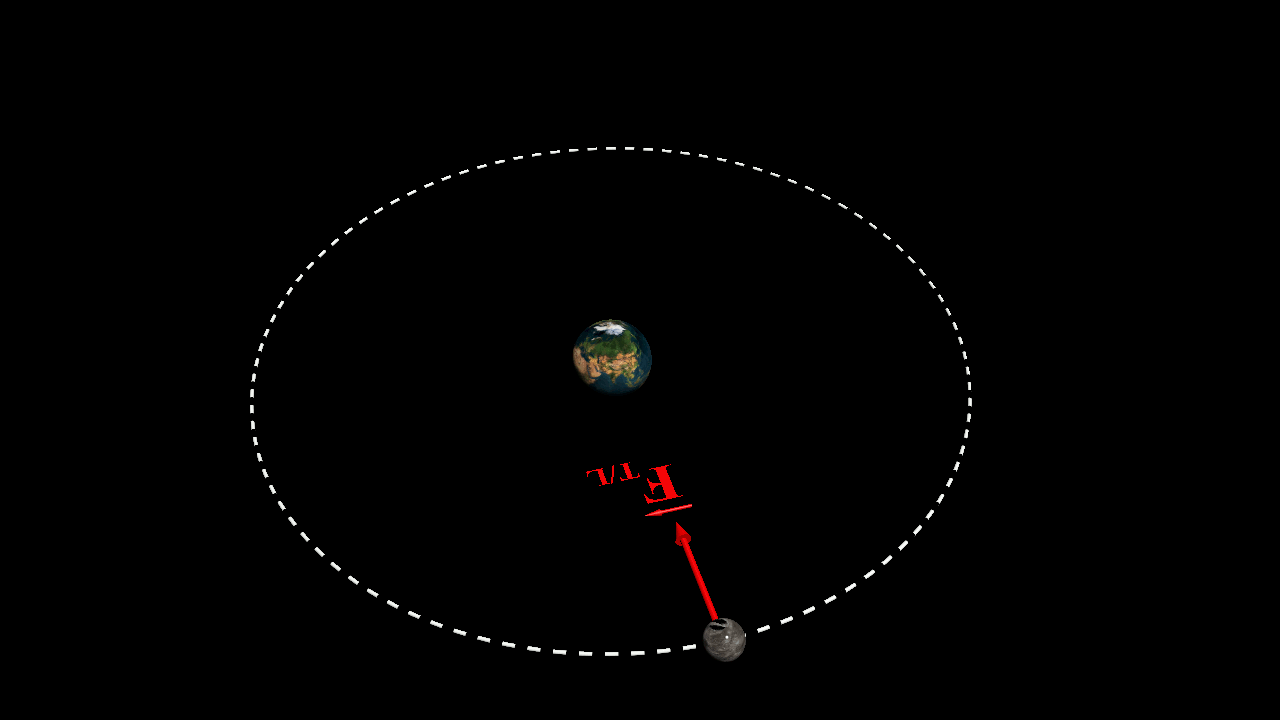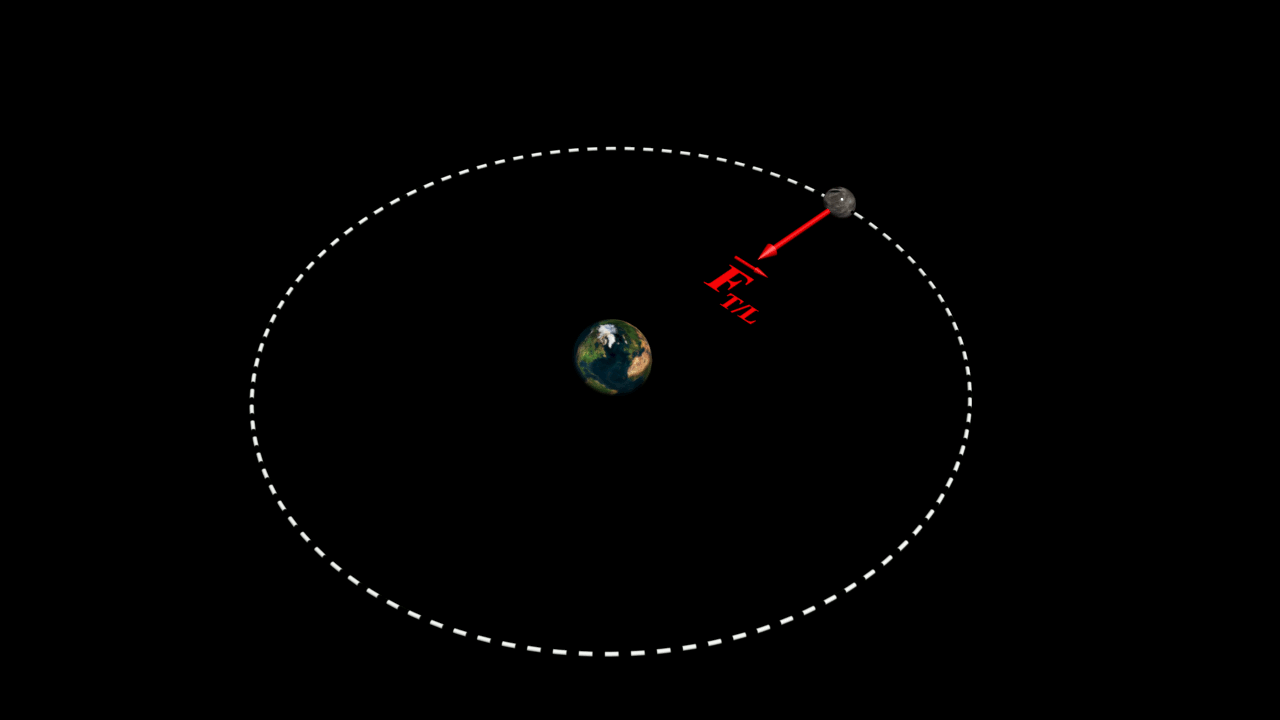
$\bullet$ Déterminer la direction et le sens de la force d'attraction de la Terre sur la Lune.

$\bullet$ Déterminer la direction et le sens de la force d'attraction de la Lune sur la Terre.

$\bullet$ Calculer la valeur de la force d'attraction correspondante.

$\bullet$ Représenter la situation en choisissant une échelle appropriée, sans souci d'échelle pour la distance.

A4. L'action réciproque.

bonjour

Dans un hangar, un ballon est lâché.

Il rebondit jusqu'à rouler et finalement s'arrêter.

Comment expliquer le fait que le ballon rebondisse ?

Doc 1 : Expérience.

A disposition :

$\bullet$ Deux dynamomètres.

$\bullet$ Une ficelle.

$\bullet$ Deux supports.

$\bullet$ A l'aide du matériel proposé, reproduire l'expérience décrite.

$\bullet$ Nommer les différentes forces exercées par chacun des sytèmes présents.

$\bullet$ Etablir un schéma représentant le situation.

$\bullet$ Pour diverses positions des supports, comparer les valeurs indiquées par les dynamomètres.

$\bullet$ Expliquer alors la situation du ballon.

$\bullet$ Tenter d'expliquer l'évolution observée.

EXERCICES P163 à 172 :

16 ; 17 ; 18 ; 20 ; 22 ; 25 ; 26 ; 29 ; 31 ; 33 ; 35 ; 36 ; 40 ; 48.

COURS

C1. Action mécanique et force.

C11. Action mécanique.

Lorsqu'un système extérieur agit sur un système est étudié, il y a une action mécanique du premier qui s'exerce sur le second.

Les actions mécaniques peuvent avoir différents effets sur le système étudié : le mettre en mouvement (action du club sur la balle), modifier sa trajectoire (action de l'aimant sur la bille) et/ou sa vitesse, ou encore le déformer (vent sur le drapeau).

C12. Action à distance et action de contact.

S'il y a contact entre les systèmes étudiés, on parle d'action mécanique de contact.

Dans le cas où il n'y a pas de contact entre les deux systèmes, on parle d'action mécanique à distance.

C13. Diagramme objets-interaction.

Le diagramme objet interaction permet de dresser schématiquement le bilan des actions mécaniques qui s'exercent sur le système étudié.

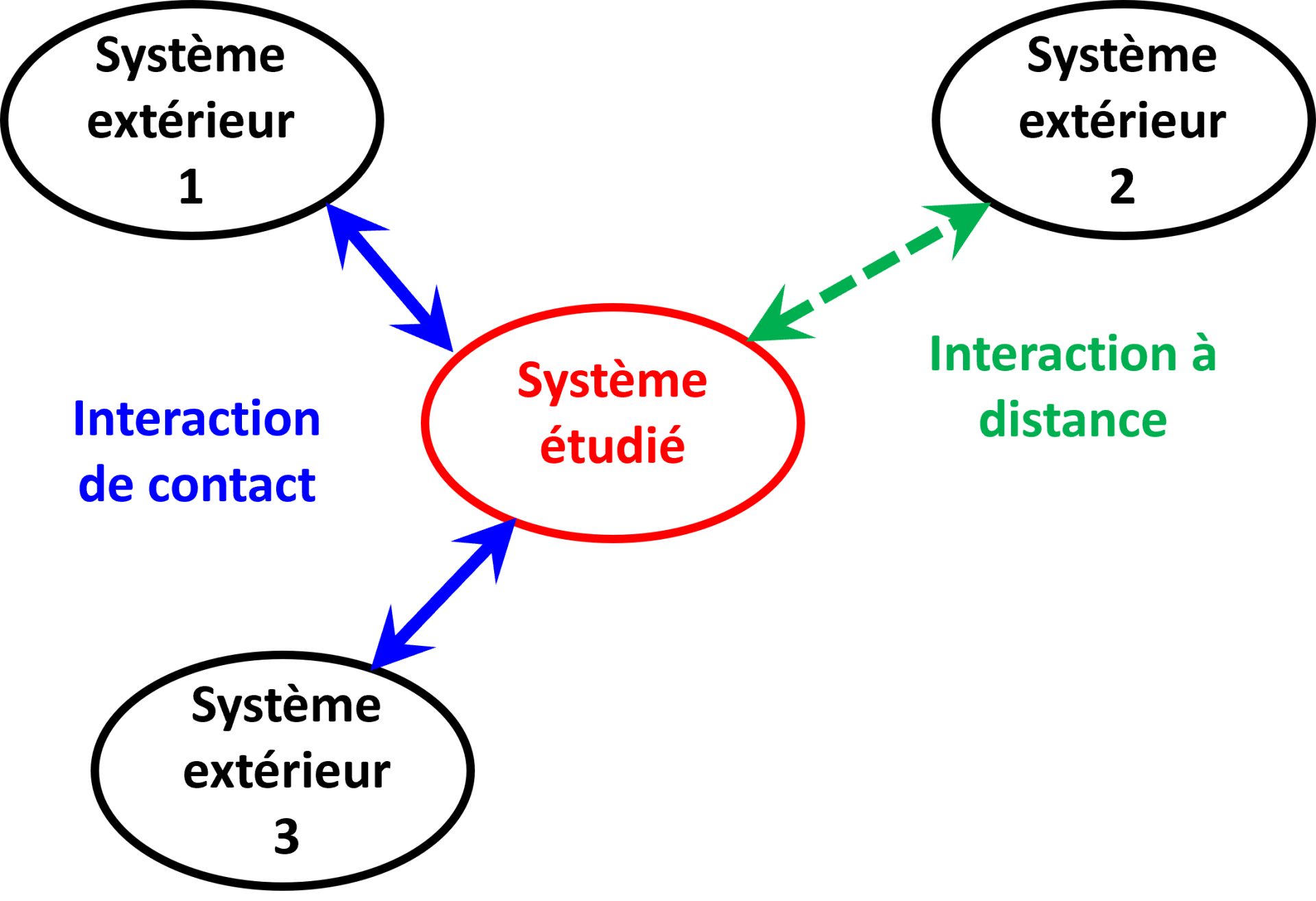C14. Modélisation de l'action mécanique.

Pour modéliser l'action mécanique d'un système A sur un système B, on la modélise par une force représentée par un vecteur $\overrightarrow{F_{A/B}}$ .

Les caractéristiques d'un vecteur $\overrightarrow{F_{A/B}}$ sont :

$\bullet$ L'origine, le point représentant le système étudié

$\bullet$ La direction, celle de l'action mécanique.

$\bullet$ Le sens, celui de l'action mécanique.

$\bullet$ La norme est proportionnelle à la valeur de la force, exprimé en Newton (N).

La valeur de la force se mesure à l'aide d'un dynamomètre.

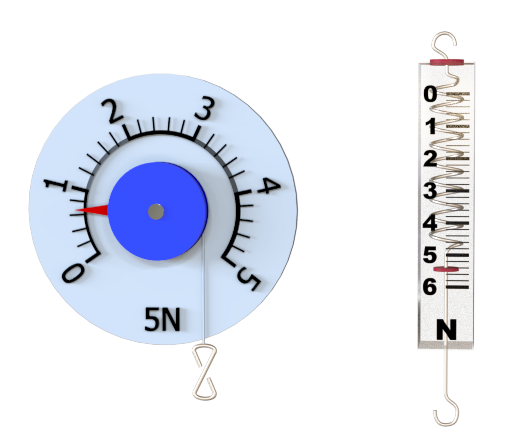C2. Exemples de forces.

C21. La force d'interaction gravitationnelle.

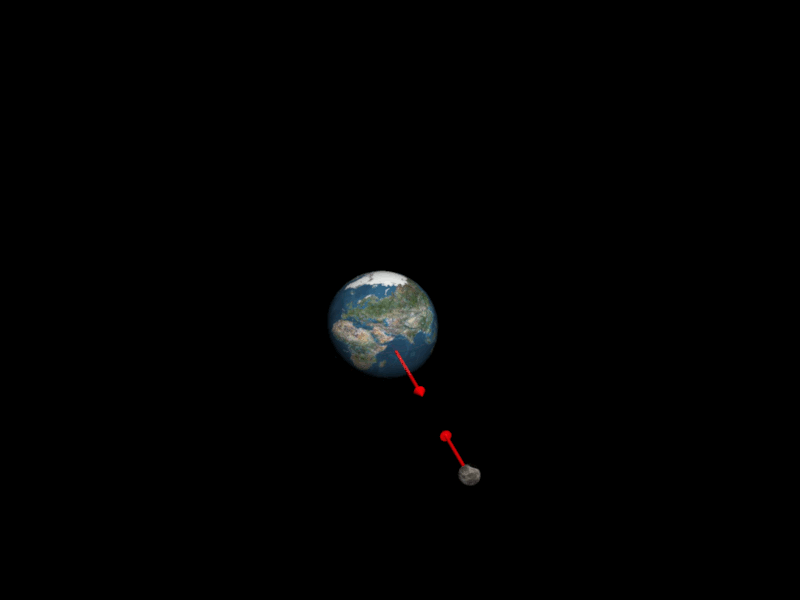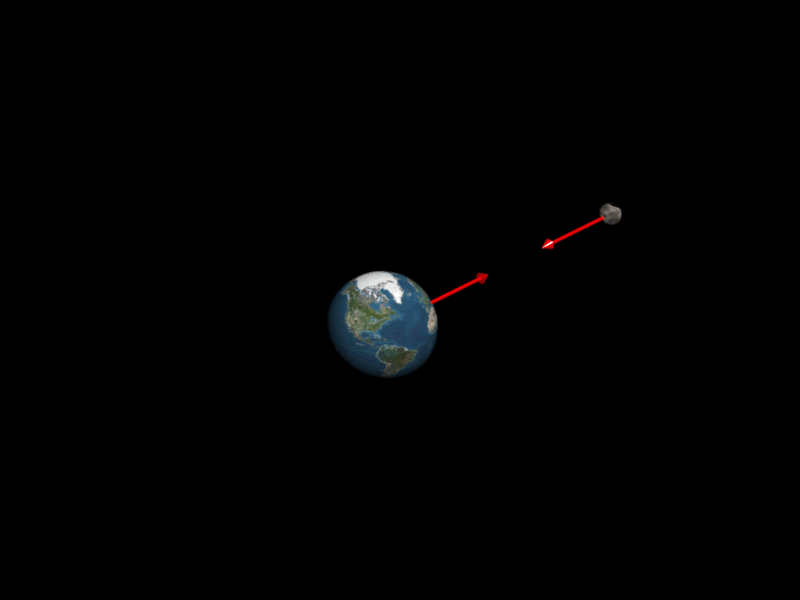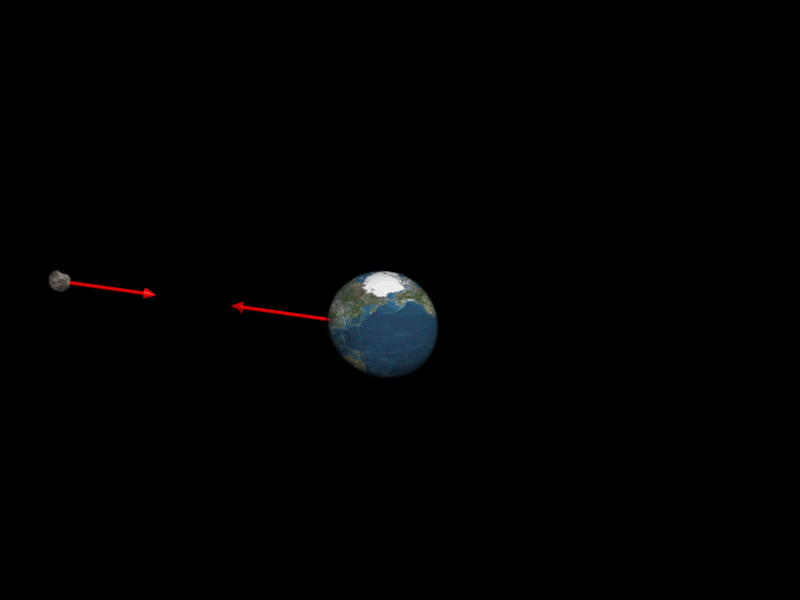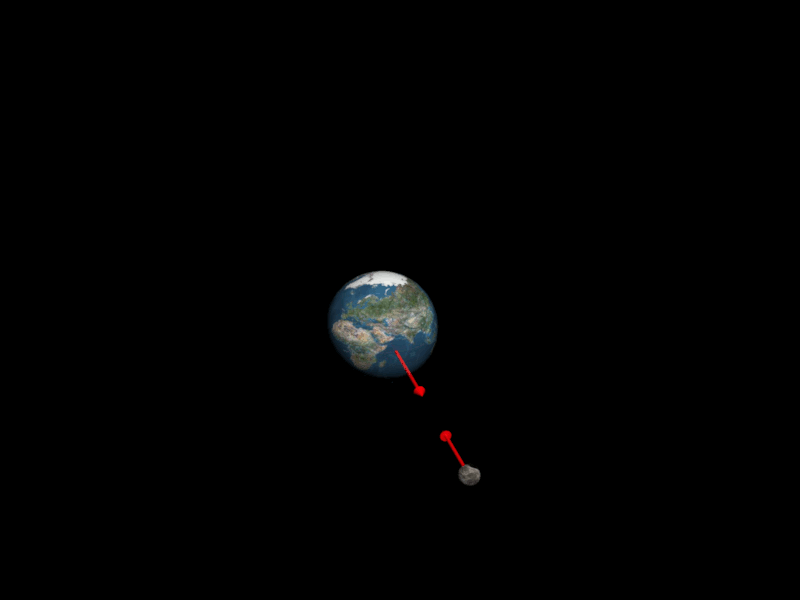
Gravite terre lune

Forces d'interactions entre la Terre et la Lune

Deux systèmes $A$ et $B$ de masses respectives $m_A$ et $m_B$, séparés d'une distance $d$, exerce l'un sur l'autre des actions mécaniques attractives modélisées par des forces appelées forces d'interaction gravitationnelle, de même intensité, de même direction, mais de sens opposés.

Ces forces d'interactions sont à l'origine des planètes autour du Soleil, et des satellites autour des planètes

$\color{red}{\overrightarrow{F_{A/B}} \ = \ - \ \overrightarrow{F_{A/B}} \ = \ G \times \dfrac{m_Am_B}{d^{ \ 2}} \times \overrightarrow{u}_{B \rightarrow A}}$

$m_A, \ m_B$ : masses en kg.

$G = 6,67.10^{ \ -11}$ : constante de gravitation universelle ($m3.kg^{ \ -1}.s^{ \ -2}$).

$d$ : distance en m.

$\overrightarrow{u}_{B \rightarrow A}$ : vecteur unitaire dirigé de B vers A.

C22. Le poids.

Un système $A$ étudié de masse $m$, se trouvant à proximité d'un astre de masse $M$ et de rayon $R$ subit l'attraction de cet astre.

L'expression du poids de ce système est :

$\color{red}{\overrightarrow{P} \ = \ m \times \overrightarrow{g}}$

$\overrightarrow{P}$ : poids du système (en N)

$m$ : masse du système en kg.

$\overrightarrow{g}$ : champ de pesanteur en $N.kg^{ \ -1}$, vertical vers le centre de l'astre

NB1 :

Par définition, cette force est la même que la force d'interaction gravitationnelle.

Or : $\overrightarrow{F_{M/m}} \ = \ G \times \dfrac{mM}{d^{ \ 2}} \times \overrightarrow{u}_{m \rightarrow M} \ = \ m \times \color{blue}{ \left ( \dfrac{GM}{d^{ \ 2}} \right )} \times \overrightarrow{u}_{m \rightarrow M} $

Donc : $\color{blue}{g \ = \ \dfrac{GM}{d^{ \ 2}}}$

Sur terre la valeur du champ de pesanteur a donc pour valeur : $g \ = \ \dfrac{6,67.10^{ \ -11} \times 5,97.10^{ \ 24}}{\left( 6380.10^{ \ 3} \right )^{ \ 2}} \ = \ 9,80 \ N.kg^{ \ -1}$

NB2 : il ne faut pas confondre masse et poids !

C23. Force exercée par un support.

La réaction $\overrightarrow R$ est l'action exercée par le support sur lobjet en contact avec le support.

$\bullet$ Elle s'applique au point de contact.

$\bullet$ Elle passe par le centre de gravité de l'objet.

$\bullet$ Elle est perpendiculaire au support.

$\bullet$ Du support vers l'objet.

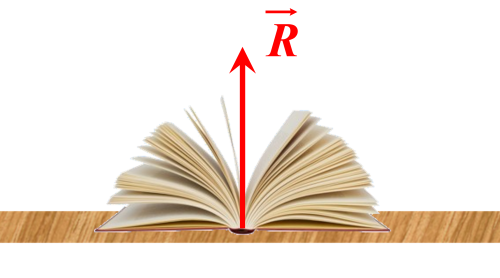
Réaction de la table sur le livre.

Réaction du sol sur le coureur

C24. Tension.

La tension $\overrightarrow T $ est la force exercée par in fil sur le système étudié.

$\bullet$ Elle s'applique au point de liaison.

$\bullet$ Elle a pour direction celle du fil.

$\bullet$ Elle est orientée du système vers le fil.

C3. Principe des actions réciproques.

La tension $\overrightarrow T$ est la force exercée par un fil sur le système étudié.

Troisième loi de Newton :

Lorsqu'un système $A$ applique une action mécanique $\overrightarrow F_{A/B}$ sur un système $B$, alors le système B applique sur le système A une force $\overrightarrow F_{B/A}$ de même intensité et de sens opposé.

$\overrightarrow F_{A/B} \ = \ - \ \overrightarrow F_{B/A}$