Statistiques à deux variables
STATISTIQUES A DEUX VARIABLES
A1. Caractéristiques d'un générateur.
Situation.
|
Un lycée vient de recevoir un lot de 500 générateurs pour équiper les Travaux Pratiques de Sciences Physiques. Les professeurs doivent s'assurer que les caractéristiques des appareils correspondent bien à celles données par le fournisseur : $\bullet$ Force électromotrice : E = 4,45 V. $\bullet$ Intensité de court-circuit : ICC = 9,0 A. |
 |
|
Un test est réalisé sur un échantillon de 20 générateurs. Chacun est branché dans un circuit électrique de résistance variable. On mesure alors la tension $U$ qu’il délivre et l’intensité $I$ dans le circuit. Les mesures relevées pour un appareils sont placées dans le tableau ci-contre. |
|
A11. Représentation des données.
$\bullet$ Placer les points dans le repère ci-dessous.

$\bullet$ Sur quelle courbe semblent se répartir les points obtenus ?
...................................................................................................................
...................................................................................................................
$\bullet$ Tracer cette courbe et déterminer son équation.
...................................................................................................................
...................................................................................................................
...................................................................................................................
...................................................................................................................
A12. Approximation à l'aide d'un tableur.
$\bullet$ A l'aide du document Excel "Activités_stat_2var.xls", effectuer une représentation du nuage de points :
![]() Activites stat 2var (10.4 Ko)
Activites stat 2var (10.4 Ko)
|
$\bullet$ Sélectionner les deux colonnes. $\bullet$ Rendez-vous dans l'onglet "insertion" $\bullet$ Sélectionner "Nuage" $\bullet$ Puis "Nuage de points avec courbe lissée" $\bullet$ Déplacer le graphique dans une nouvelle feuille. $\bullet$ Cliquer "droit" sur la courbe. $\bullet$ Sélectionner "ajouter une courbe de tendance". $\bullet$ Dans l'onglet qui s'affiche, cocher : "linéaire". $\bullet$ Afficher l'équation sur le graphique. |
A13. Conclusion.
$\bullet$ Comparer les résultats obtenus à l'aide des deux méthodes.
...................................................................................................................
...................................................................................................................
...................................................................................................................
$\bullet$ Valider ou non les caractéristiques affichées par le fournisseur :
Le professeur acceptera l'appareil si la tolérance de 5% sur les caractéristiques du fournisseur n’est pas dépassée.
La force électromotrice $E$ est la tension donnée pour une intensité $I \ = \ 0 \ A$.
L’intensité de court-circuit $Icc$ est donnée pour un tension $U \ = \ 0 \ V$.
L'appareil est-il accepté ?
Que représente physiquement le coefficient directeur de la droite ?
...................................................................................................................
...................................................................................................................
...................................................................................................................
...................................................................................................................
...................................................................................................................
A14. Coefficient de corrélation.
$\bullet$ En utilisant le logiciel Excel, déterminer le coefficient de corrélation $R^2$.
...................................................................................................................
...................................................................................................................
A15. En utilisant la calculatrice.
$\bullet$ Reprendre l'étude en utilisant la mode "stat" de votre calculatrice.
$\bullet$ Comparer les résultats.
...................................................................................................................
...................................................................................................................
A2. Prévision temporelle.
Situation.
Le tableau suivant correspond aux émissions de gaz à effet de serre (en millions de tonnes équivalent $CO_2$) relevées en France.
|
 |
A21. Point moyen.
Déterminer les coordonnées $\overline {x_G}$ (moyenne des années) et $\overline {y_G}$ (moyenne des émissions) du point moyen.
...................................................................................................................
...................................................................................................................
A22. Droite d'ajustement.
On suppose que le modèle est assimilable à une variation affine du temps. L'équation de la droite obtenue a pour coefficient directeur $– 3,33$ et passe par le point $G$ déterminé précédemment.
$\bullet$ Déterminer l'équation de cette droite.
...................................................................................................................
...................................................................................................................
...................................................................................................................
...................................................................................................................
$\bullet$ Déterminer l'équation de cette droite.
...................................................................................................................
...................................................................................................................
...................................................................................................................
...................................................................................................................
$\bullet$ Prévoir alors la quantité de gaz à effet de serre en 2025.
...................................................................................................................
...................................................................................................................
...................................................................................................................
...................................................................................................................
$\bullet$ En quelle année cette émission sera-t-elle nulle ?
...................................................................................................................
...................................................................................................................
...................................................................................................................
...................................................................................................................
A23. En utilisant les outils numériques.
A23a. Avec Excel.
$\bullet$ Retrouver les résultats précédents en utilisant le tableur Excel (Activités.xls)
$\bullet$ Imprimer les résultats sur une seule page.
A23b. Avec la calculatrice.
|
$\bullet$ Sélectionner le mode "Statistiques" $\bullet$ Initialiser les colonnes. $\bullet$ Entrer les valeurs du tableau dans les colonnes.
$\longrightarrow$ Onglet CALC $\longrightarrow$ Onglet Set $\bullet$ "1Var XList : List1" $\bullet$ "1Var XFreq : List2" $\bullet$ "2Var XList : List1" $\bullet$ "2Var XFreq : List2" $\bullet$ "2Var YFreq : 1" |
$\longrightarrow$ EXE
$\longrightarrow$ Onglet 2-Var : retrouver les coordonnées du point moyen.
...................................................................................................................
...................................................................................................................
$\longrightarrow$ EXE
$\longrightarrow$ Onglet REG
$\longrightarrow$ Onglet X
$\longrightarrow$ Onglet ax+b : retrouver l'équation de la droite d'ajustement.
...................................................................................................................
...................................................................................................................
A23c. En utilisant un programme "Python".
|
Dans le programme fourni, placer les données de l'activité au bon endroit. Faire afficher l'estimation pour l'année 2025. Comparer avec les outils précédents.
|
 |
COURS
C1. Statistiques à deux variables.
C11. Définition.
|
Une série statistique à deux variables est obtenue lors de l'étude conjointe de deux séries quantitatives. Si les valeurs prises par le premier caractère sont : $\left (x_1;x_2;.....;x_n \right )$ et celles prises par le premier caractère sont : $\left (y_1;y_2;.....;y_n \right )$ L'ensemble des $n$ couples $\left (x_i;y_i \right )$ définit alors les données de la série statistiques à deux variables $X$ et $Y$. |
Exemple: On étudie la taille $y$ (en cm) d'un nourrisson et son âge $x$ (en mois).
|
Rq: Les deux séries sont souvent représentées sous forme d'un tableau.
C12. Représentation.
|
Dans un repère orthogonal, l'ensemble des $n$ points $M_i$ de coordonnées $\left ( x_i;y_i \right )$ forment un nuage de points représentant cette série statistique. |
Exemple (suite) : 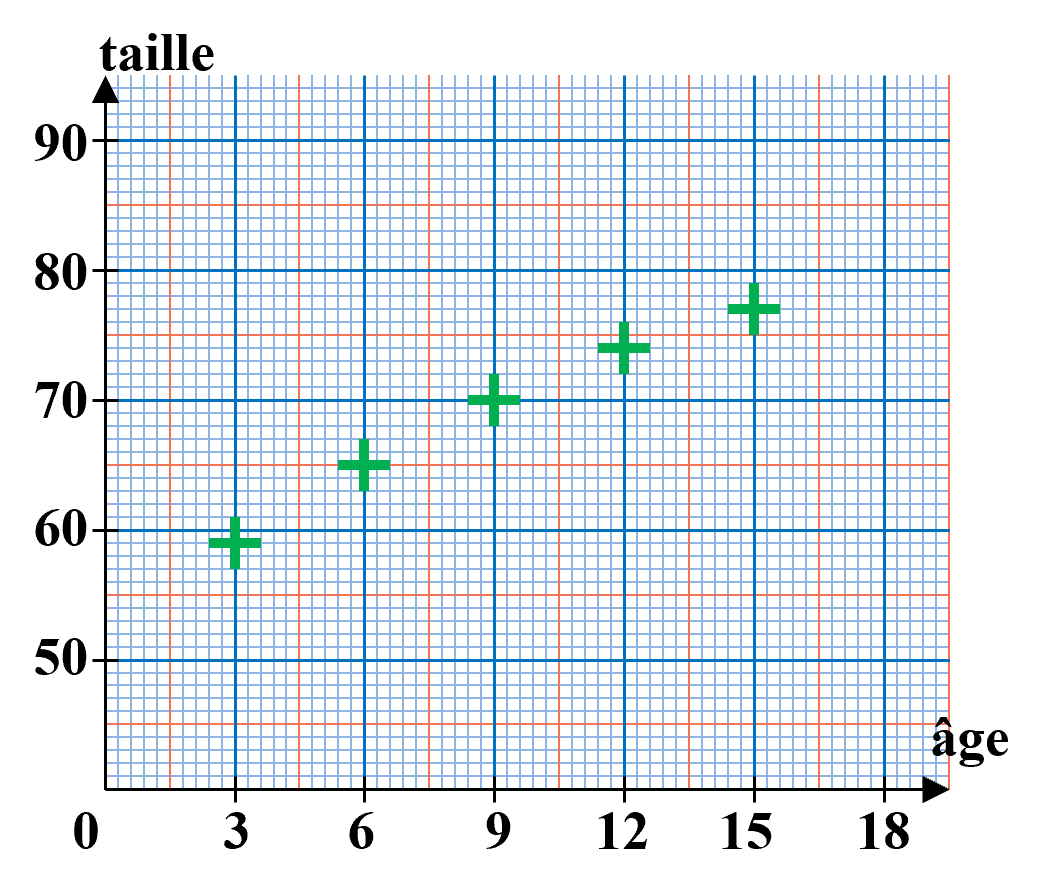 |
C2. Point moyen.
|
Le point moyen G d'un nuage de points $M_i \left ( x_i ; y_i \right )$ a pour coordonnées $\left ( \overline x \ ; \ \overline y \right )$ où $\overline x$ et $\overline y$ sont les moyennes des séries $\left ( x_i \right )$ et $\left ( y_i \right )$ : $\overline x \ = \ \dfrac{\sum_{i=1}^{n} x_i}{n} \ = \ \dfrac{x_1+x_2+....+x_n}{n}$ $\overline x \ = \ \dfrac{\sum_{i=1}^{n} y_i}{n} \ = \ \dfrac{y_1+y_2+....+y_n}{n}$ |
Exemple (suite) : $\overline x \ = \ \dfrac{3+6+9+12+15}{5} \ = \ 9$ $\overline y \ = \ \dfrac{59+65+70+74+77}{5} \ = \ 69$ 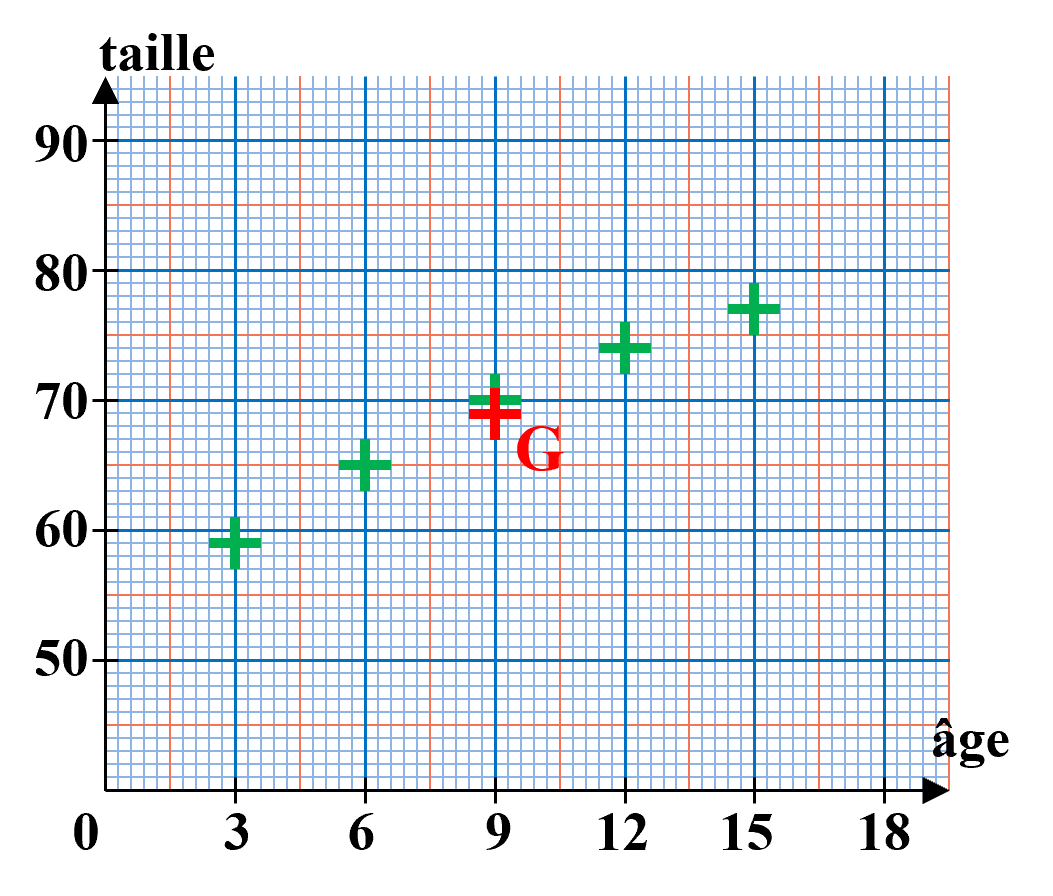 |
C3. Ajustement affine.
C31. Envisager un ajustement affine.
|
Lorsque le nuage de points $M_i \left ( x_i \ ; \ y_i \right)$ a une forme allongée, on peut envisager une relation affine entre $x$ et $y$. Réaliser un ajustement affine consiste à déterminer l'équation de la droite qui passe au plus près de tous les points du nuage. La relation liant $x$ et $y$ est du type : $f : x \mapsto y \ = \ ax+b$ La droite d'ajustement affine passe toujours par le point moyen. L'équation $y \ = \ ax+b$ de cette droite donne de façon approchée une relation entre les abscisses et ordonnées du nuage de points. |
Exemple (suite) : 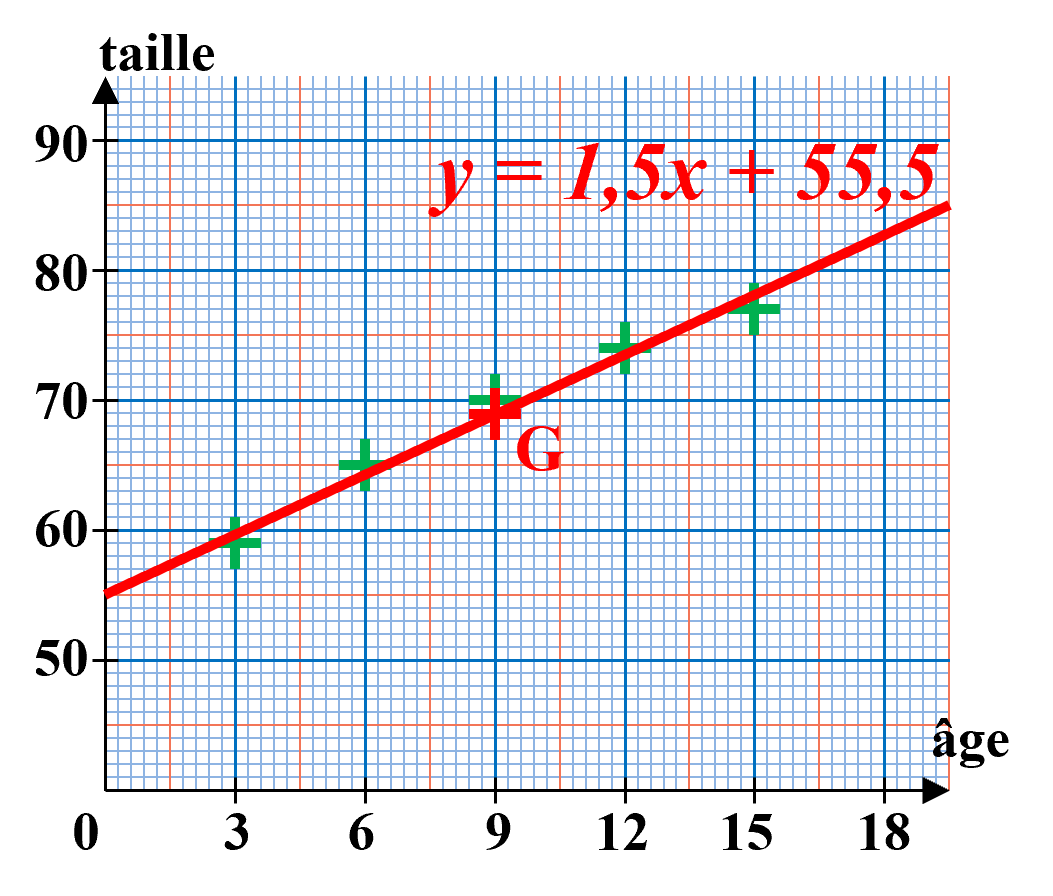 |
C32. Utilisation.
|
Une fois l'ajustement affine réaliser, la relation entre $y$ et $x$ permet d'envisager les valeurs "suivantes" de $y$ pour $x$ donné. |
Exemple (suite) : A 18 mois, la taille du nourrisson serait : $1,5 \times 18 + 55,5 \ = \ 82,5 \ cm$ |
Ajouter un commentaire
