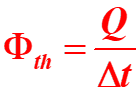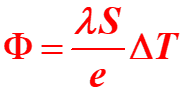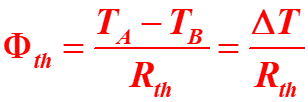Thermodynamique
ACTIVITES
A1 Calorimétrie.
L’eau liquide est une phase condensée. Lorsqu’elle reçoit un transfert thermique, sa température augmente et donc son énergie interne augmente aussi. Comment relier la variation d’énergie interne de l’eau à sa variation de température ?
A11 Expérience.

|
Pour mesurer les transferts thermiques mis en jeu au cours d’échanges thermiques ou de transformations chimiques, on peut utiliser un calorimètre. Il s’agit d’une enceinte thermiquement isolée du milieu extérieur. Un calorimètre comprend généralement un système d’agitation et un thermomètre. Un calorimètre est dit idéal si son contenu n’échange pas d’énergie thermique avec l’extérieur. On se placera dans ce cas. Peser précisément une masse meau d'eau distillée à température ambiante correspondant à un volume d’environ 140 mL. La verser dans un calorimètre contenant une résistance chauffante à immersion (thermoplongeur), un agitateur et un thermomètre. |
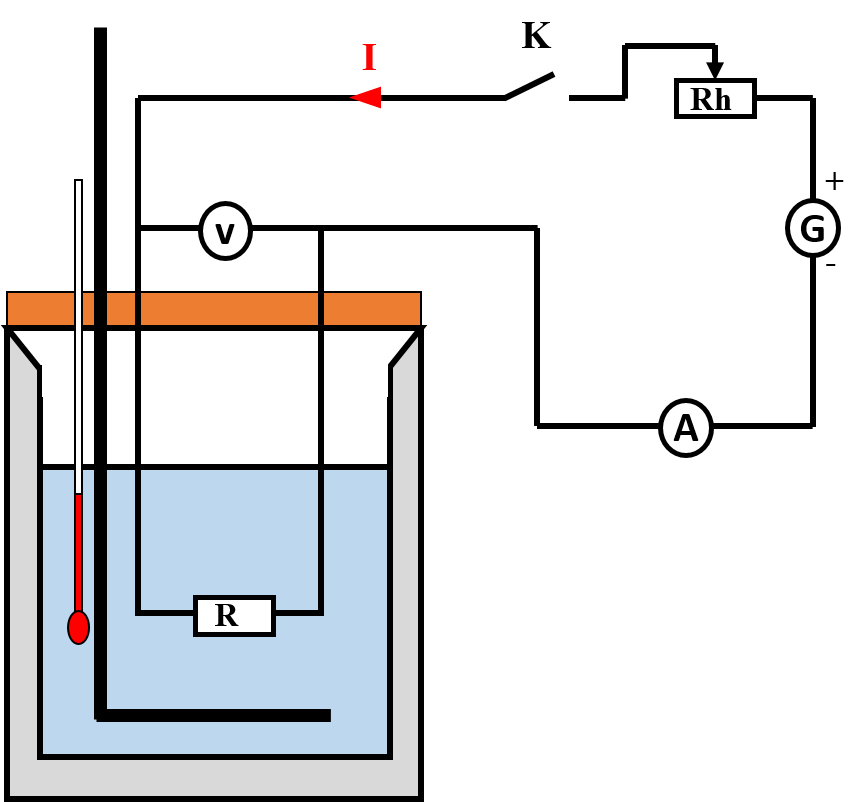 |
· Réaliser le circuit représenté sur le schéma précédent en réglant le générateur de tension à 6 V.
· Régler l’ampèremètre sur le plus fort calibre (10 A continu).
Attention :
Le rhéostat présente 2 bornes noires A et B tel que la résistance RAB = Rmax =100 ?.
Il comporte également une borne rouge C reliée à un curseur. La résistance entre la borne C et B est comprise entre : 0 ? < RBC < RAB = 100 ? suivant la position du curseur. En reliant le circuit entre les bornes R et C et en déplaçant le curseur on peut donc faire varier la résistance dans le circuit et par conséquent l’intensité qui le traverse.
· Faire vérifier le montage.
· Fermer l'interrupteur, déplacer ensuite le curseur de manière à régler l’intensité du courant à une valeur d’intensité i = 2 A. Noter la valeur de l’intensité exacte du courant sur votre compte rendu.
· Ouvrir l’interrupteur. Mesurer la température initiale θ0 de l'eau.
· Fermer l’interrupteur en déclenchant simultanément le chronomètre.
· Mesurer et noter la tension U aux bornes de la résistance.
· Effectuer un suivi temporel sur 15 minutes de la grandeur Δθ = θ - θ0 (variation de la température).
A12 Exploitation des résultats.
|
Info1 : la variation d’énergie interne ΔUS d’un système macroscopique fermé S, qui échange avec le milieu extérieur du travail W et du transfert thermique Q est égale à : ΔUS = WS + QS. WS et QS sont comptés positivement s’ils sont reçus par le système S du milieu extérieur. WS et QS sont comptés négativement s’ils sont cédés par le système S au milieu extérieur. Info2 : Soit U la tension aux bornes d’une résistance et I l’intensité qui la traverse. La puissance électrique P consommée par une résistance est P = U.I. Le travail électrique reçu par la résistance pendant la durée Δt est W = P. Δt. Info3 : la variation d’énergie interne d’une phase condensée X (solide ou liquide) ΔUX de masse mx et de capacité thermique massique Cx dont la température varie de Δθ s’écrit : ΔUX = mX.Cx.Δθ
|
A121. On considère le système {résistance} : schématiser les échanges énergétiques entre ce système et l’extérieur en indiquant la nature et le signe des transferts d’énergies.
A122. Exprimer le travail électrique Wres reçu par la résistance en fonction de U, I et de la durée Δt.
A123. On admet que tout le travail électrique Wres reçu par la résistance est intégralement transformé en énergie thermique Qres : que vaut alors la variation d’énergie interne de la résistance notée ΔUres ?
A124. Soit le système {eau + calorimètre} : ce système reçoit le transfert thermique cédé par la résistance.
A124a. Schématiser les échanges énergétiques entre ce système et l’extérieur.
A124b. En déduire une relation entre la variation d’énergie interne ΔUeau+cal du système et Δt.
A125. Dans un tableur, faire calculer les valeurs de ΔUeau+cal à partir des valeurs du tableau.
A126. Dans le tableur, tracer le graphe ΔUeau+cal en fonction de Δθ Commenter l’allure du graphe.
A127. Déterminer la valeur et l’unité du coefficient directeur k du graphe précédent.
A128. On note respectivement cAl et ceau les capacités thermiques massique du calorimètre (en aluminium) et de l’eau (en J.g-1.C-1). Exprimer, littéralement, les transferts thermiques QCal et Qeau reçus par le calorimètre, (de masse mcal) et l’eau. En déduire l’expression de ΔUeau+cal .
A129. Montrer alors que k = mcal.cAl + meau.ceau. En déduire une valeur expérimentale de ceau.
(Donnée : cAl = 0,897 J.g-1.°C-1 ; la masse du calorimètre est mcal = 31,3 g).
A1210. Les tables donnent ceau = 4,18 J.g-1.°C-1. Comparer la valeur expérimentale obtenue à celle des tables. Comment expliquer une éventuelle différence entre les deux valeurs ?
A1211. Rassembler les résultats de tous les groupes et calculer une valeur moyenne ainsi que l’écart-type σn-1.
L’incertitude de répétabilité sur ceau est donnée par la relation : 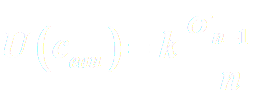 , où n est le nombre de mesures de ceau et k le coefficient de Student donné dans le tableau ci-dessous.
, où n est le nombre de mesures de ceau et k le coefficient de Student donné dans le tableau ci-dessous.
| n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| k95% | 12,7 | 4,30 | 3,18 | 2,78 | 2,57 | 2,45 | 2,37 | 2,31 | 2,26 | 2,23 | 2,20 | 2,18 | 2,16 | 2,15 | 2,13 |
| k99% | 63,7 | 9,93 | 5,84 | 4,60 | 4,03 | 3,71 | 3,50 | 3,36 | 3,25 | 3,17 | 3,11 | 3,06 | 3,01 | 2,98 | 2,95 |
A1212. En considérant un niveau de confiance de 99 % exprimer ceau sous la forme : ceau = ceau.moy ± U(ceau).
A2 Transferts thermiques.

A21 Les trois types de transferts thermiques.
Document 1 :
| Caractéristiques de transferts thermiques | |
| A |
Transfert d’énergie qui existe pour tout corps. Il a lieu sans contact physique et correspond à de l’énergie électromagnétique. |
| B |
Transfert d’énergie par contact dans un matériau ou à l’interface entre deux milieux. Il a lieu lorsqu’une différence de température existe entre deux régions d’un système. L’énergie des particules se communique de proche en proche. |
| C | Transfert d’énergie provoqué par le mouvement d’ensemble d’un fluide (liquide ou gaz). Il peut être naturel ou forcé. |
Document 2 :
|
Schéma1
|
Schéma2
|
Document 3 : Les trois types de transferts thermiques.
- Conduction
- Convection
- Rayonnement
Document 4 :
 |
Expérience de l’étoile métallique. On dépose un morceau de paraffine au bout de chaque branche. Observer. Interpréter. |
A211. Associer à chacun des schémas 1 et 2 le type de transferts thermiques illustré ainsi que les caractéristiques correspondantes.
| Schéma | Type de transfert |
Caractéristique de transfert (A, B ou C) |
| 1 | ||
| 2 |
A212. Les trois types de transferts thermiques sont mis en jeu au niveau des zones ou des équipements suivants d’une maison : murs extérieurs, toiture, vitres, radiateur électrique. Justifier les trois types de transferts thermiques pour les murs extérieurs et pour le radiateur électrique.
A213. En utilisant vos connaissances de première S (loi de Wien), expliquer pourquoi une caméra thermique illustre les transferts thermiques par rayonnement ?
A214. Document 4. Décrire l’expérience, réalisée par le professeur, avec les différents métaux illustrant les transferts thermiques par conduction dans un métal les l’influence du métal.
A22 Conductivité thermique d'un matériau.
|
||||
|
Conductivité thermique |
Béton plein |
Bois de sapin |
Paille |
Laine de verre |
Plâtre A13 |
Béton armé |
Brique pleine |
| λ | 1,7 | 0,14 | 0,050 | 0,040 | 0,25 | 2,2 | 1,0 |
A221. Justifier l’unité de conductivité précisée ci-dessus.
A222. Classer les matériaux cités dans le tableau du moins isolant au plus isolant.
A223. Comparons la conductivité du bois à celle du carrelage.
A223a. En touchant le carrelage et le bois, indiquer lequel semble le plus froid.
A223b. A l’aide d’une caméra thermique, mesurer leurs températures. Vos doigts sont-ils de bons capteurs de température ?
A223c. Si un matériau paraît plus froid, c’est que le flux thermique du doigt vers le matériau est plus élevé. En utilisant la formule donnée, comparer les conductivités thermiques du carrelage et du bois. Lequel est le meilleur isolant ?
A23 Flux thermique et résistance thermique.
|
Document 1 : Résistance thermique. La résistance thermique R d’une paroi traduit la résistance aux transferts thermiques. Elle est liée au flux thermique Φ en W à travers la paroi et à la différence de température ?T entre les 2 faces par :
On définit également la résistance thermique surfacique Rs, telle que : Le flux thermique Φ s’écrit donc aussi :
Dans le cas d’une paroi constituée de plusieurs couches de matériaux différents, les résistances thermiques s’additionnent. |
|
||||||
|
Document 3 : Le châlet pyrénéen
|
A231a. Déterminer l’unité de la résistance thermique Rth.
A231b. Justifier la phrase suivante : "Plus la valeur de la résistance thermique d’une paroi est grande, plus celle-ci est isolante."
A231c. Pour une paroi constituée d’un seul matériau, établir l’expression de la résistance surfacique Rs en fonction de certaines caractéristiques de la paroi et du matériau.
A232. Retrouver la valeur de la résistance thermique surfacique indiquée sur l’étiquette (doc2), sachant que la valeur de la conductivité thermique non arrondie est 0,03702 W/(m.K) ; les règles d’arrondi à respecter sont indiquées dans le document 2.
|
A233. Dans l’exemple ci-contre, e représente l’épaisseur de béton nécessaire pour que la paroi ait les mêmes performances thermiques qu’une paroi idéale de laine minérale de 5,0 cm d’épaisseur. A233a. Déterminer cette épaisseur. A233b. Commenter la phrase suivante : "Les matériaux lourds de maçonnerie ne constituent jamais une isolation acceptable". |
 |
A234. À l’aide des différents documents, calculer la valeur du flux thermique par conduction, à travers les murs extérieurs du chalet auquel se rapporte le document 3, lorsque la température intérieure est de 18°C et la température extérieure de 0°C. Pour simplifier, on ne tiendra pas compte des surfaces des portes et des parois vitrées.
A235. Pour une plaque de verre d’épaisseur 5 mm et de surface 30 cm², on obtient Φ = 5,0 W, TA =21,1°C et TB = 13,5°C.
A235a. En déduire la résistance thermique de la plaque de verre.
A235b. Déterminer la conductivité thermique λ du verre.
COURS
C1 Energie interne.
C11 Définition.
On appelle énergie interne l'ensemble des formes d'énergie présentes au sein d'un système. On la note U.
L'énergie interne est due en particulier:
- Aux interactions existant entre les particules qui constituent le système (énergie potentielle microscopique).
- A l'énergie cinétique des particules qui constituent le système.
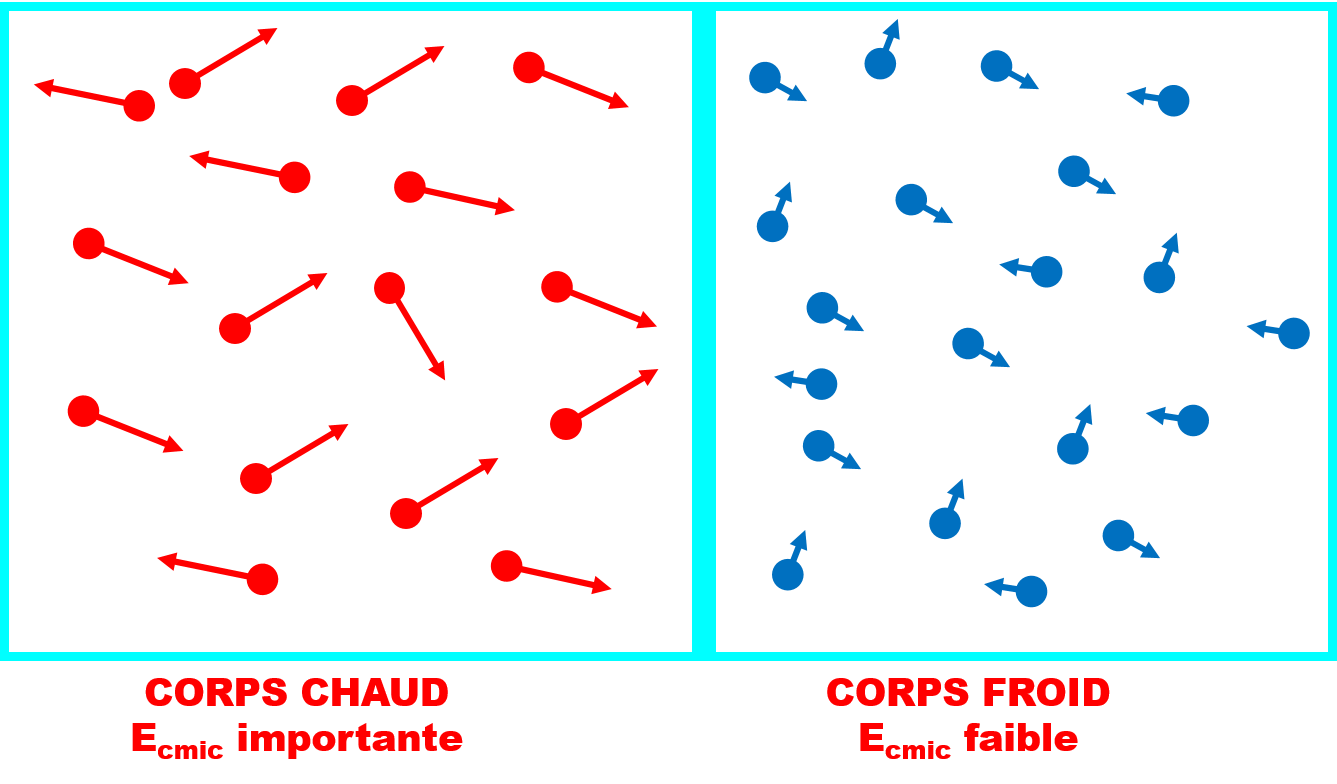
Remarque 1 : La température caractérise l'agitation thermique, c'est à dire à l'énergie cinétique microscopique des particules qui constituent le système. Si la température T augmente, alors Ecmic augmente et l'énergie interne U augmente.
Remarque 2 : L'énergie potentielle microscopique est due aux interactions gravitationnelle, électromagnétique, forte et faible entre les particules qui constituent le système. On distingue les énergies potentielles microscopiques chimique, électrique, magnétique et nucléaire.
C12 Variation d'énergie d'un système.
· La variation d'énergie totale du système est la somme de la variation de son énergie interne et de la variation de son énergie mécanique :
ΔEtot = ΔEm + ΔU
· Lorsque l'énergie mécanique du système est constante, la variation d'énergie totale est uniquement due à la variation d'énergie interne.
Si ΔEm = 0 alors : ΔEm = ΔU
C13 Modes de transfert d'énergie.
Le travail W et le transfert thermique Q sont des modes de transfert d'énergie ; leur signe dépend du sens du transfert entre le système et l'extérieur. La chaleur Q est un mode "désordonné" de transfert peu contrôlable la partie travail W est, elle, "contrôlable".
La variation d'énergie interne ΔU d'un système est la conséquence d'échanges d'énergie avec l'extérieur par travail W par transfert thermique Q. Si l'énergie mécanique du système est constante :
ΔU = Q + W = Qreçu - Qcédée + Wreçu - Wcédé
Remarque 1 : ΔU , Q et W s'expriment en Joules (J)
Remarque 2 :
· Si ΔU > 0 , le système reçoit de l’énergie du milieu extérieur.
· Si ΔU < 0 , le système fournit de l’énergie au milieu extérieur.
C2 Transferts thermiques.
C21 Variation d'énergie interne.
Lorsqu’un système condensé (solide ou liquide) évolue d’un état initial vers un état final, la variation ΔU de son énergie interne est proportionnelle à sa variation de température ΔT.
|
· C : capacité thermique du système (J.kg-1) · ΔT : variation de température (K) · ΔU : variation d'énergie interne (J) |
C22 Mécanisme du transfert thermique.
|
Lors d’un transfert thermique, la température du corps chaud diminue et la température du corps froid augmente. Lorsque Tcorps chaud = Tcorps froid, les deux objets sont à l'équilibre thermique. |
 |
Remarque 1 : Le transfert d'énergie par chaleur s'effectue toujours du corps chaud vers le corps froid. Les transferts s'effectuent toujours de systèmes d'états microscopiques plus désordonnés vers des systèmes d'état microscopique moins désordonnés.
Remarque 2 : Les transferts thermiques sont une cause d'irréversibilité : il arrive qu'un système évolue par transfert thermique vers un état final sans pouvoir spontanément revenir à son état initial.
C23 Modes de transferts thermiques.
On peut interpréter les transferts thermiques dans la matière à l'échelle microscopique suivant trois modes principaux :
- la conduction
- la convection
- le rayonnement.
|
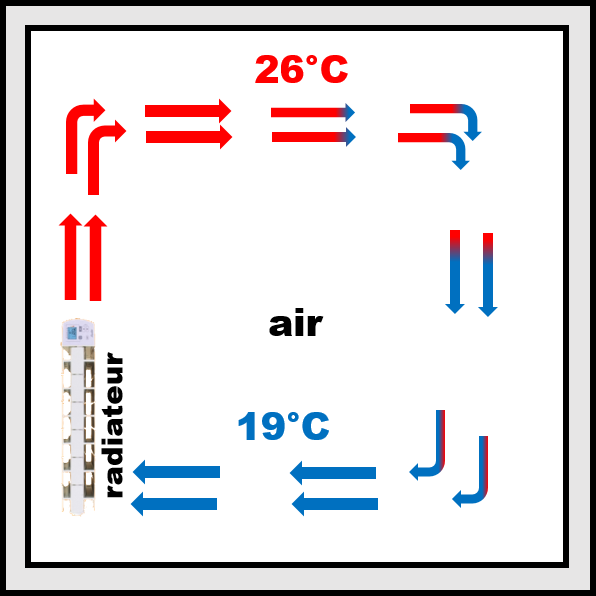
C23a La conduction. Le transfert thermique par conduction est généré au niveau microscopique par des interactions entre des entités en contact direct. C'est le seul mode de transfert thermique dans les solides. Les chocs multiples provoquent la propagation de l'énergie du corps chaud vers le corps froid. |
 |
|
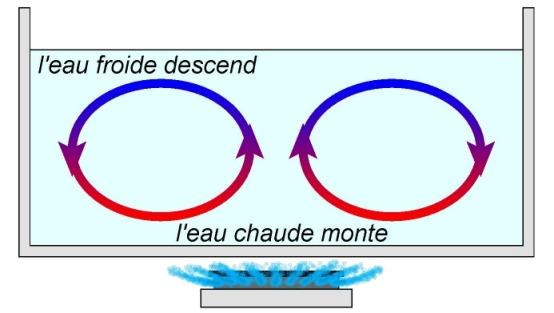
C23b La convection. Ce mode de transfert thermique est spécifique aux systèmes fluides (gaz ou liquides).
Définition : Le transfert thermique par convection est généré par un mouvement global des entités microscopiques à l'intérieur d'un système. Il y a transport de matière. |
 |
C23c Le rayonnement thermique.
Le transfert thermique par rayonnement est généré par l’absorption ou l’émission d’un rayonnement électromagnétique. Seul moyen de transfert d'énergie dans le vide.
C3 Flux interne.
 |
A travers une paroi, lors d'un transfert thermique entre un corps chaud de température TA et un corps froid de température TB, séparés par un matériau, le corps le plus chaud cède de l'energie Q au corps le plus froid au travers de la paroi. Cette transformation n'a lieu que dans un sens elle est irréversible. Le flux thermique ou puissance thermique Φth caractérise la vitesse du transfert thermique Q, pendant une durée Δt , au sein d'un système ou entre différents systèmes. C'est la chaleur Q échangée par unité de temps :
|
Ce flux est proportionnel à la différence de température TA-TB.
Le flux thermique Φ (en Watt) à travers une paroi plane de surface S, d’épaisseur e, constituée d’un seul matériau de conductivité λ, est proportionnel à la différence de température ?T entre les deux faces :
|
|
· λ en W.m-1.K-1 · e en m · S en m2 · Φth en W · T en K · Rth en K.W-1 : résistance thermique |
Ajouter un commentaire


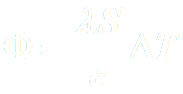
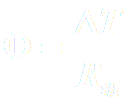
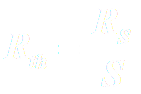 . C’est la résistance thermique de la paroi pour une surface de 1 m2.
. C’est la résistance thermique de la paroi pour une surface de 1 m2.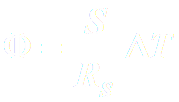 avec S la surface de la paroi.
avec S la surface de la paroi.