Fonction dérivée

MathJax.Hub.Config({tex2jax: {inlineMath: [['$','$'], ['\$','\$']]}});

ACTIVITES

A0. Rappels.

A01. Tracer de droites.

Dans le repère ci-contre, tracer les droites dont les équations sont données ci-dessous :

$D_1 \ : \ y=2x-2$

Coefficient directeur : ...........

Ordonnée à l'origine : ............

$D_1$	A	B
$x$
$y$

$D_2 \ : \ y=-x+3$

Coefficient directeur : ...........

Ordonnée à l'origine : ............

$D_2$	C	D
$x$
$y$

$D_3 \ : \ y=3$

Coefficient directeur : ...........

Ordonnée à l'origine : ............

$D_3$	E	F
$x$
$y$

$D_1 \ : \ x=-3$

Coefficient directeur : ...........

Ordonnée à l'origine : ............

A02. Déterminer graphiquement l'équation d'une droite.

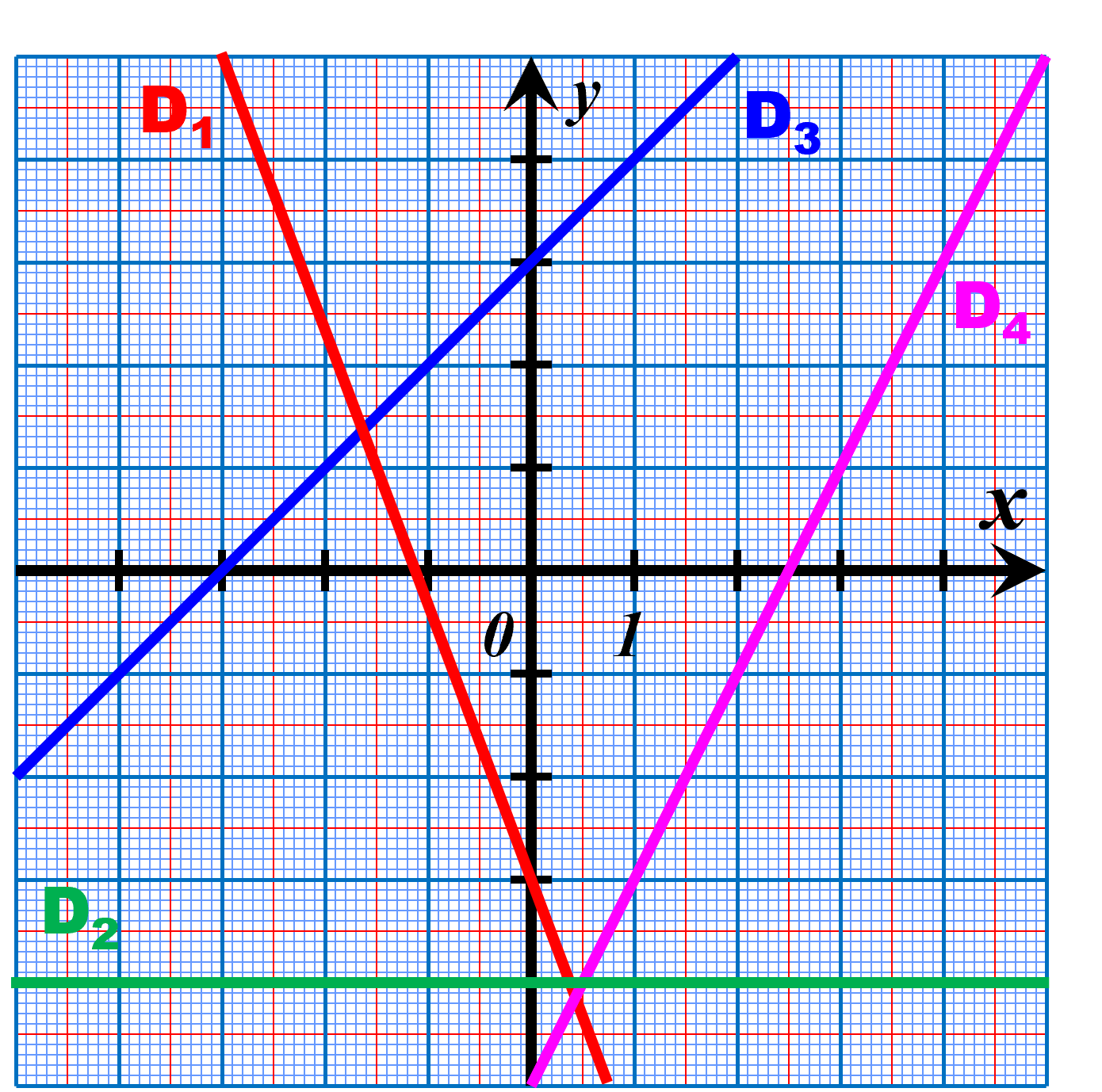Par lecture graphique, donner l’équation de chaque droite représentée ci-contre.

Droite	Ordonnée à l'origine.	Coefficient directeur	Equation
$D_1$
$D_2$
$D_3$
$D_4$

A1. Tangente.

A11. Pour un cercle.

$\bullet$ Dessiner ci-contre un cercle $\cal C$ et de rayon $r \ = \ 3 \ cm$.

$\bullet$ Soit un point A de ce cercle.

$\bullet$ Tracer la tangente à $\cal C$ en A.

$\bullet$ Expliquer la procédure.

.............................................................................

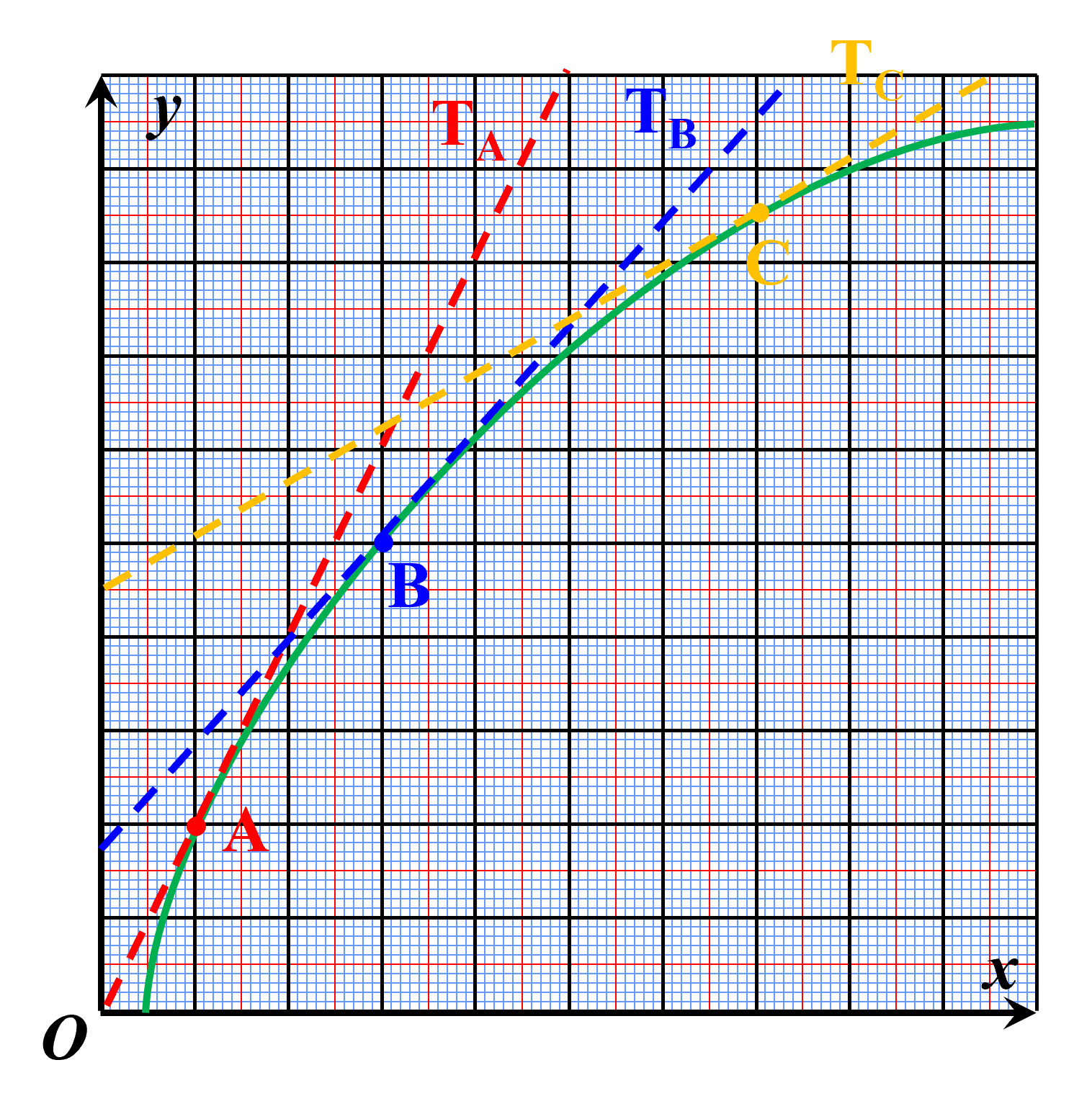
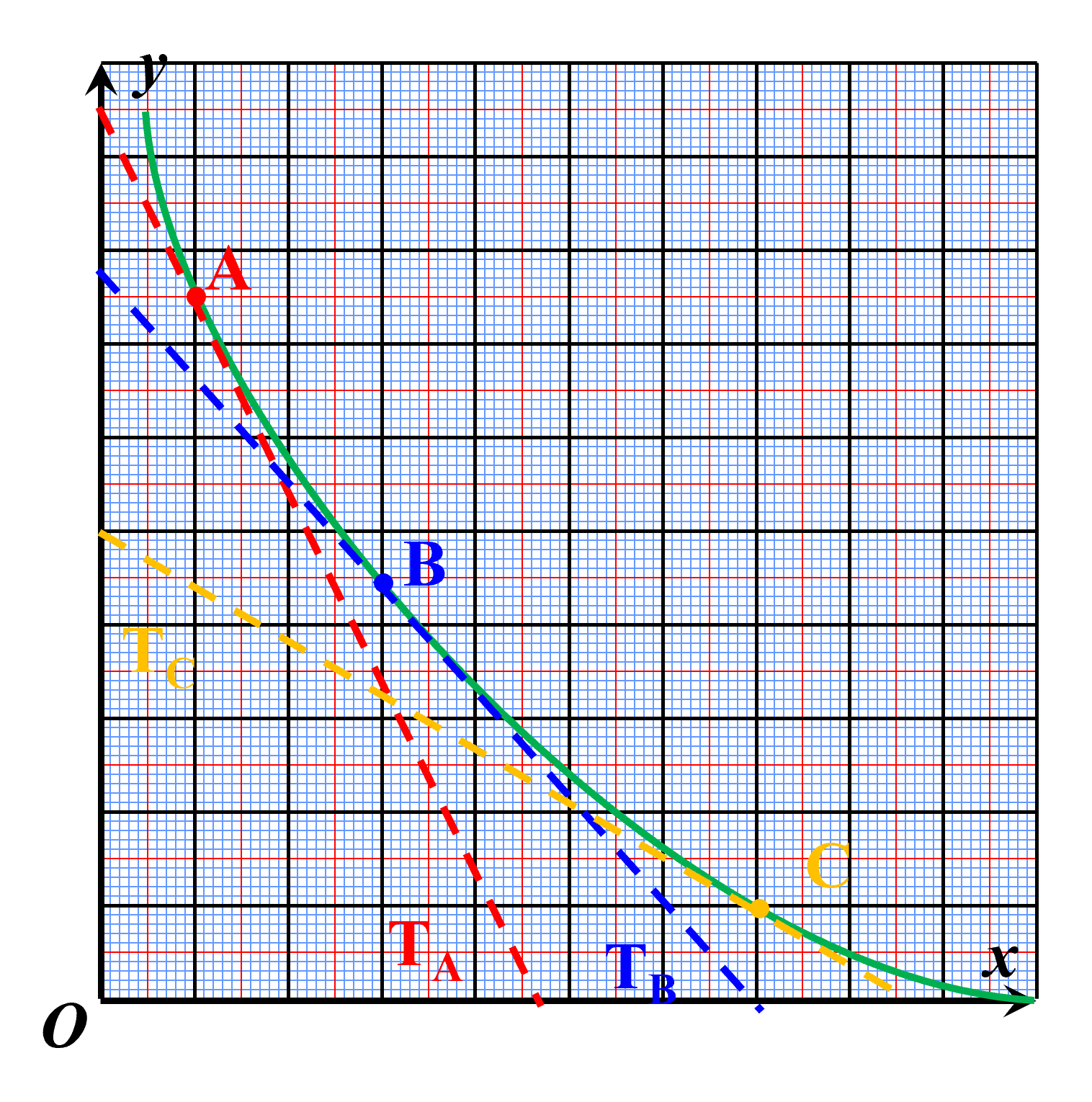
A12. Avec d'autres courbes.

Pour chaque courbe $\cal C$ ci-dessous, indiquer quelle semble être la tangente à la courbe en A.


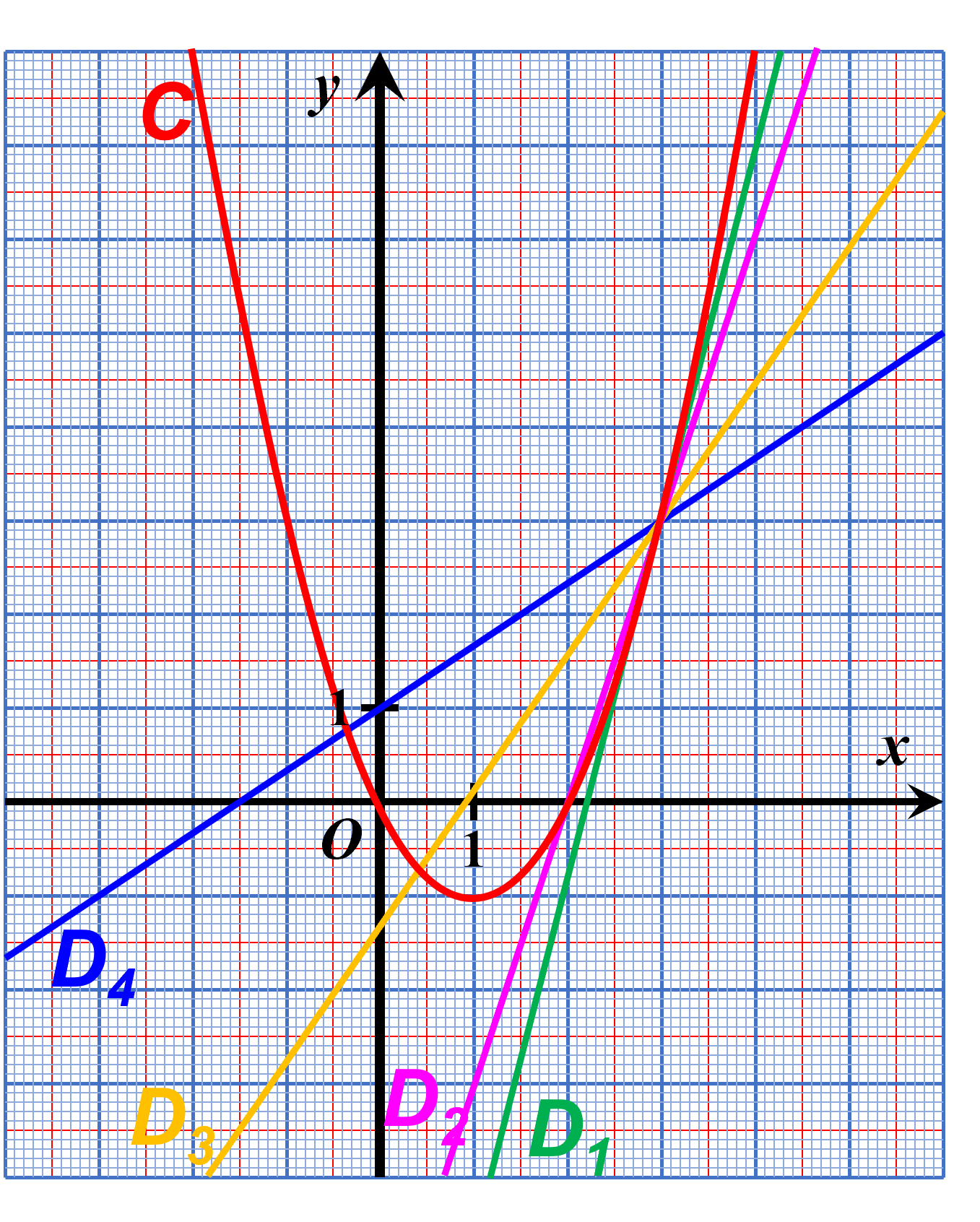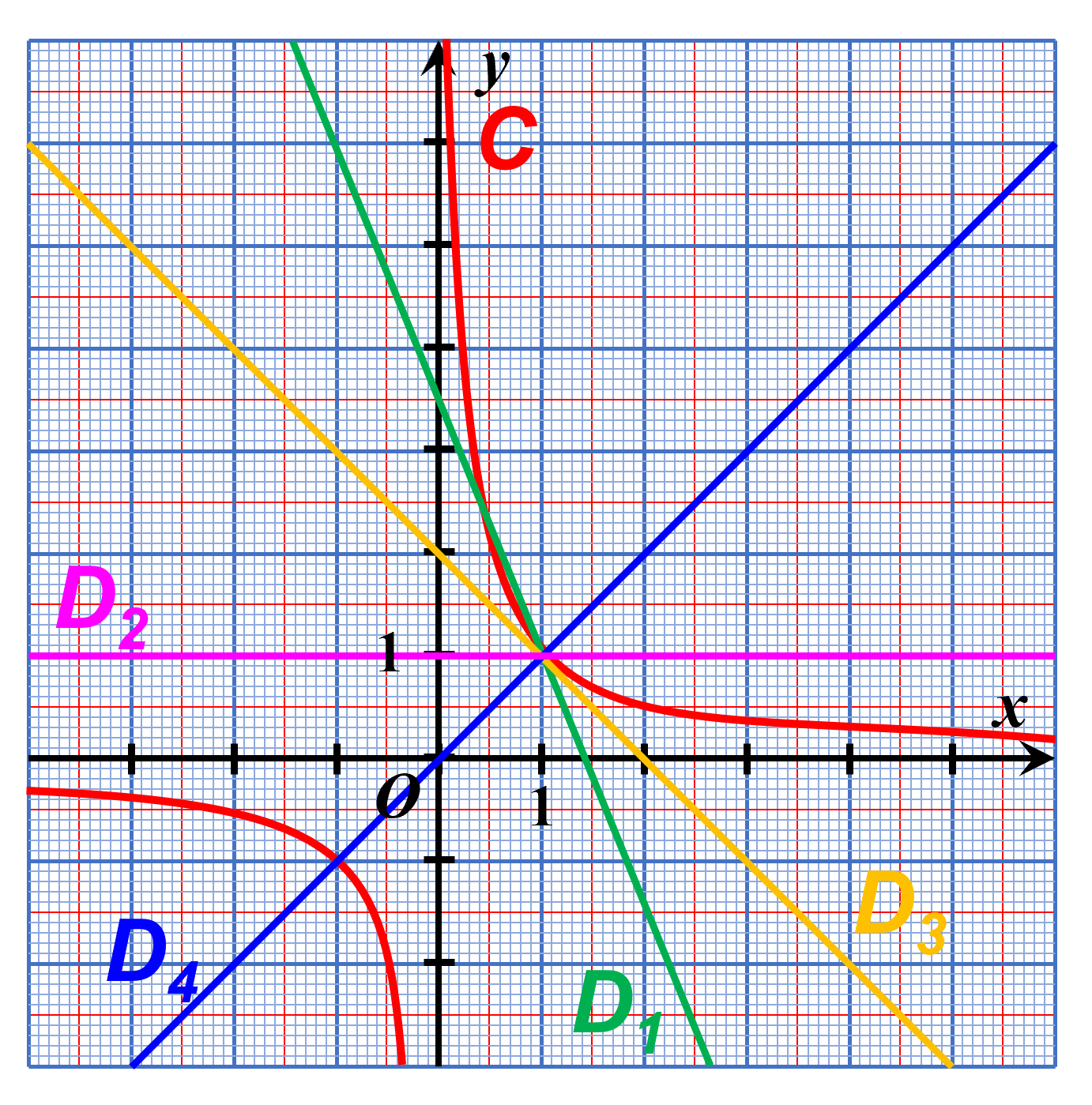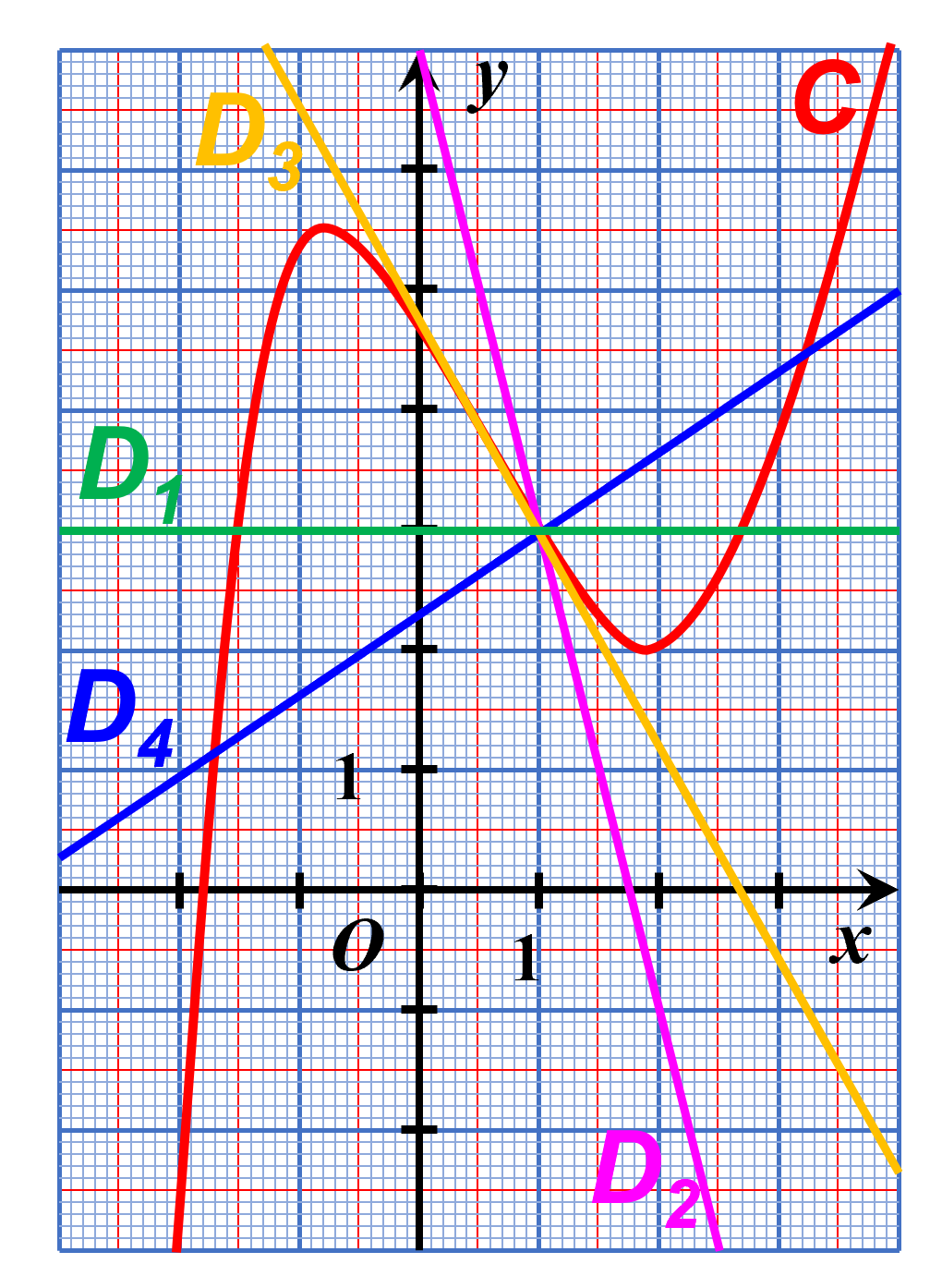$\Box \ D_1$ $\Box \ D_2$ $\Box \ D_3$ $\Box \ D_4$	$\Box \ D_1$ $\Box \ D_2$ $\Box \ D_3$ $\Box \ D_4$	$\Box \ D_1$ $\Box \ D_2$ $\Box \ D_3$ $\Box \ D_4$

A2. Nombre dérivé et fonction dérivée.

A21. Expérience.

$\bullet$ En utilisant le logiciel Geobebra, tracer dans un même repère, les droites suivantes :

$D_1 \ : \ y=-8x-16$	$D_5 \ : \ y=-4x-4$	$D_{10} \ : \ y=x-0,25$	$D_{14} \ : \ y=5x-6,25$
$D_2 \ : \ y = -7x-12,25$	$D_6 \ : \ y = -3x-2,255$	$D_{11} \ : \ y = 2x-1$	$D_{15} \ : \ y = 6x-9$
$D_3 \ : \ y = -6x-9$	$D_7 \ : \ y = -2x-1$	$D_{12} \ : \ y = 3x-2,25$	$D_{16} \ : \ y = 7x-12,25$
$D_4 \ : \ y = -5x-6,25$	$D_8 \ : \ y = -x-0,25$	$D_{13} \ : \ y = 4x-4$	$D_{17} \ : \ y = 8x-16$
$D_9 \ : \ y = 0$

$\bullet$ Quelle est la fonction de référence qui semble apparaître dans la zone au-dessus de ces droites ?

...........................................................................................................

$\bullet$ Tracer la courbe $C$ de cette fonction dans le même repère pour vérifier l’hypothèse ci-dessus.

$\bullet$ Que représentent ces droites pour la fonction déterminée ? ……………………………………………

Exemples

$\bullet \ D_1$ est ………………………………. à $C$ en $x =$ ……………….

$\bullet \ D_4$ est ………………………………. à $C$ en $x =$ ……………….

$\bullet \ D_12$ est ………………………………. à $C$ en $x =$ ……………….

$\bullet \ D_15$ est ………………………………. à $C$ en $x =$ ……………….

A22. Nombre dérivé et fonction dérivée.

A22a. Nombre dérivé.

$\bullet$ En utilisant toujours la fonction précédente,$f\ : \ x \ \mapsto \ f(x)=x^2$, compléter le tableau suivant :

$x$	$-4$	$-3$	$-2x$	$-1$	$0$	$1$	$2$	$3$	$4$
Coefficient directeur de la tangente.

Définition :

Le coefficient directeur de la tangente à la courbe représentative $C$ d'une fonction $f$ en un point d'abscisse $a$ est appelé nombre dérivé de la fonction $f$ en $a$.

On le note : $f'(a)$

$\bullet$ A l'aide de la calculatrice, toujours pour la fonction $f\ : \ x \ \mapsto \ f(x)=x^2$.

$x$	Equation de la tangente.	Nombre dérivé
$-3$
$-2$
$-1$
$0$
$1$
$2$
$3$

A21b. Fonction dérivée.

$\bullet$ A quoi vous fait penser le tableau complété à la question A21a ?

...................................................................................................

Définition :

La fonction associant le coefficient directeur de la tangente à la courbe représentative $C$ d'une fonction $f$ en tout point d'abscisse $x$ appelée fonction dérivée de la fonction $f$.

On la note : $f'$

$\bullet$ A l'aide de l'étude précédente, donner l'expression de la fonction $f\ : \ x \ \mapsto \ f(x)=x^2$.

...................................................................................................

A22. Equation de la tangente.

$\bullet$ Dans le logiciel Geogebra, en prenant la fonction $f \ : \ x \ \mapsto f(x)=x^2$, pour x allant de - 4 à 3, compléter le tableau suivant :

$a$	Equation de la tangente	$f'(a) \times \left ( x-a \right ) +f(a)$
$-3$
$-2$
$-1$
$0$
$1$
$2$
$3$

$\bullet$ Pour une fonction $f$, l'équation de la tangente à la courbe représentative $C$ en un point d'abscisse $a$ est :

...................................................................................................

A3. Variations d'une fonction.

A31. $f : x \mapsto f(x) = x^2$

$x$	$-3$	$-2$	$-1$	$0$	$1$	$2$	$3$
Signe de $f'$
Variations de $f$

A32. $f : x \mapsto f(x) = -2x^2$

$x$	$-3$	$-2$	$-1$	$0$	$1$	$2$	$3$
Signe de $f'$
Variations de $f$

A33. Conclusion.

...................................................................................................................

A4. Etude des variations d'une fonction complexe.

A41. Dériver $k \times f(x)$ et dériver $f(x)+g(x)$.

A41a. $f(x) \ = \ -2x$

$\bullet$ Compléter le tableau :

$x$	$-4$	$-3$	$-2$	$-1$	$0$	$1$	$2$	$3$	$4$
$f'(x)$

$\bullet$ Proposer l'expression de la fonction dérivée de $f\ : \ x \ \mapsto \ f(x)=-2x$

...................................................................................................................

A41b. $f(x) \ = \ -2x-12$

$\bullet$ Compléter le tableau :

$x$	$-4$	$-3$	$-2$	$-1$	$0$	$1$	$2$	$3$	$4$
$f'(x)$

$\bullet$ Proposer l'expression de la fonction dérivée de $f\ : \ x \ \mapsto \ f(x)=-2x-12$

...................................................................................................................

A41c. $f(x) \ = \ 2x^2+12$

$\bullet$ Compléter le tableau :

$x$	$-4$	$-3$	$-2$	$-1$	$0$	$1$	$2$	$3$	$4$
$f'(x)$

$\bullet$ Proposer l'expression de la fonction dérivée de $f\ : \ x \ \mapsto \ f(x)=2x^2+12$

...................................................................................................................

A41d. $f(x) \ = \ 2x^2-2x-12$

$\bullet$ Compléter le tableau :

$x$	$-4$	$-3$	$-2$	$-1$	$0$	$1$	$2$	$3$	$4$
$f'(x)$

$\bullet$ Proposer l'expression de la fonction dérivée de $f\ : \ x \ \mapsto \ f(x)=2x^2-2x-12$

...................................................................................................................

A42. Conclusion.

...................................................................................................................

A5. Application.

Etude de la fonction $f(x) \ = \ \dfrac{2}{3}x^3-x^2-12x+12$

A51. $f(x) \ = \ x^3$

$\bullet$ Compléter le tableau :

$x$	$-4$	$-3$	$-2$	$-1$	$0$	$1$	$2$	$3$	$4$
$f'(x)$

$\bullet$ Proposer l'expression de la fonction dérivée de la fonction $ x \ \mapsto \ x^3$

...................................................................................................................

A51b. Fonction dérivée.

$\bullet$ A l'aide des conclusions de l'activité précédentes, déterminer l'expression de $f'(x)$

...................................................................................................................

A52. Variations.

$\bullet$ Déterminer le signe de $f'(x)$.

$\bullet$ Compléter le tableau suivant.

$x$
Signe de $f'$
Variations de $f$

$\bullet$ Vérifier votre travail avec Geogebra et votre calculatrice.

COURS

C1. Tangente à une courbe.

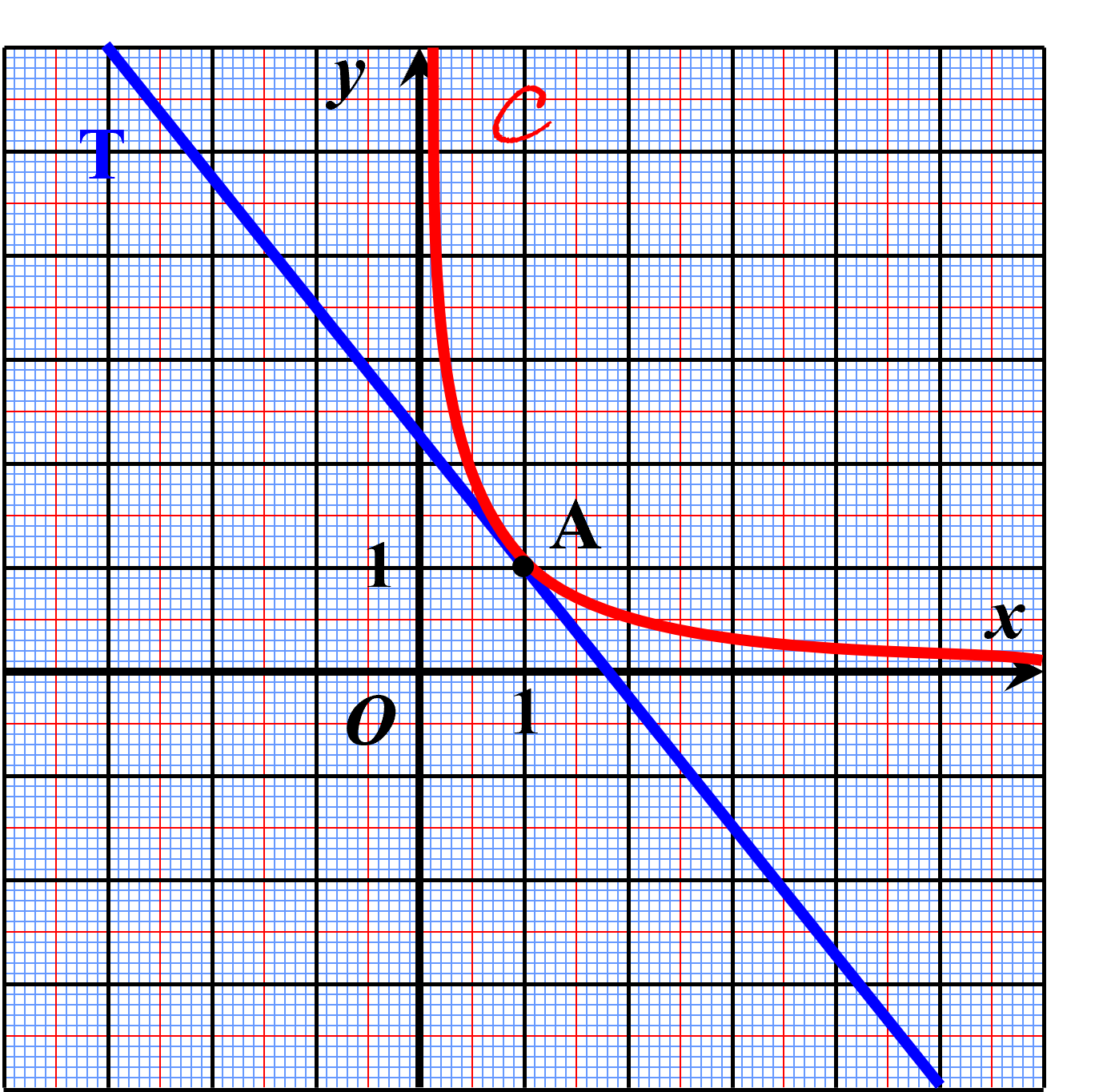
C11. Définition.

Le mot “tangente” vient du latin “tangere”, qui signifie “toucher”.

La tangente à une courbe en un point donné est la droite qui “touche” la courbe au plus près, au voisinage de ce point.

Ci-contre, D est la tangente à $\cal C$ en A.

C12. Nombre dérivé.

Soit $f$, une fonction de courbe représentative $\cal C_f$.

On appelle nombre dérivé de la fonction en $x_A$, le coefficient directeur de la tangente $T$ à $\cal C_f$ au point $A$ d’abscisse $x_A$.

Ce nombre est noté : $f’(x_A)$

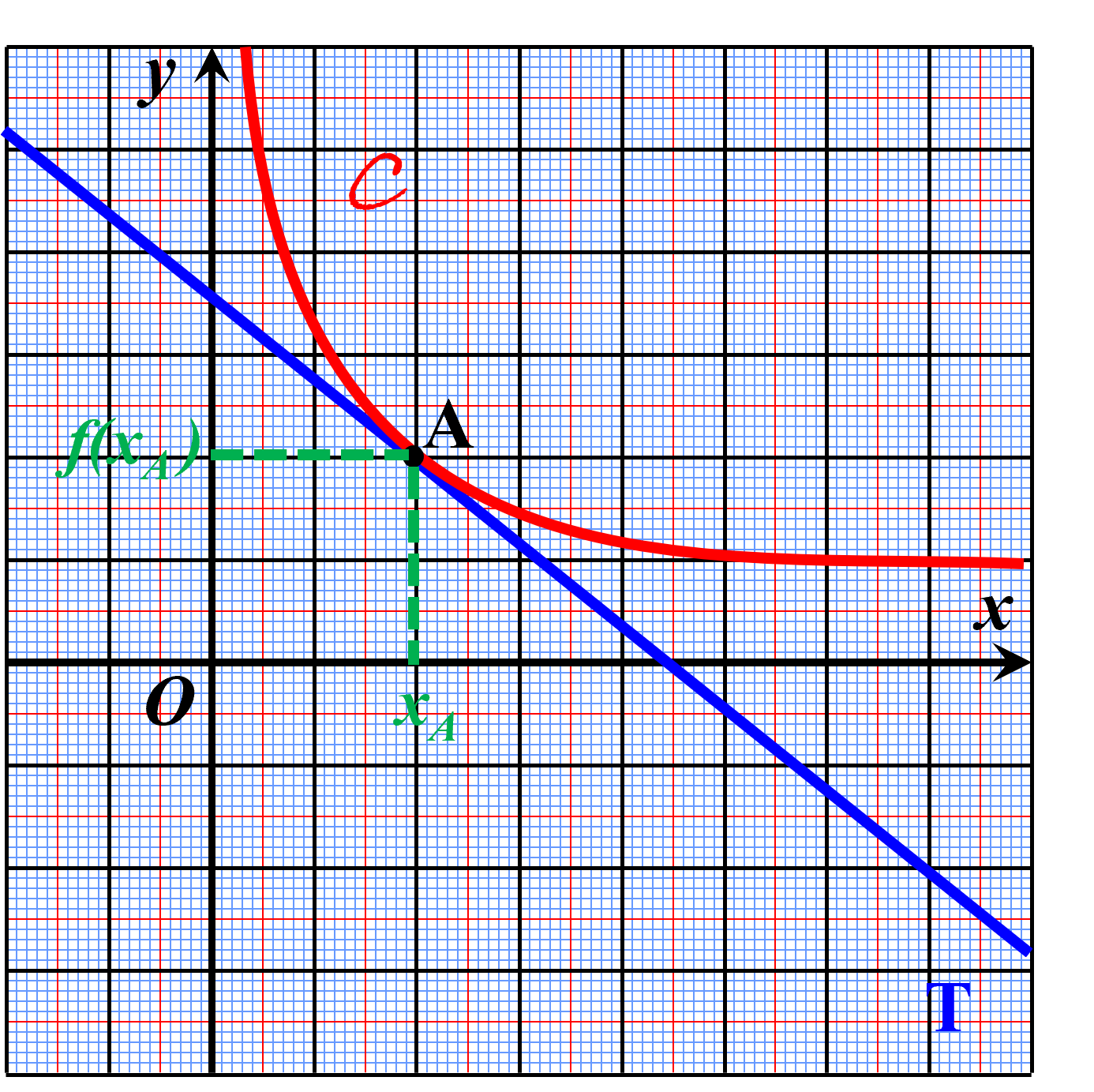C13. Equation de la tangente.

L’équation de la tangente à $\cal C_f$ en $x_A$ est :

$y=f'(x_A) \times \left ( x-x_A \right ) + f(x_A)$

C2. La fonction dérivée.

Définition.

On considère une fonction $f$ définie sur un intervalle $I$.

La fonction dérivée notée $f'$ de la fonction $f$ est la fonction qui à tout nombre $x$ de l'intervalle $I$ associe le nombre dérivé de la fonction $f$.

$f' : \ x \ \mapsto f'(x)$.

C3. Relation entre le sens de variation et le signe de la dérivée.

Fonction croissante.

Fct croissante

En tout point de la courbe, les tangentes ont toutes un coefficient directeur positif :

Pour tout x de l'intervalle $I$ : $f'(x) \geq 0$

Fonction décroissante.

Fct decroissante

En tout point de la courbe, les tangentes ont toutes un coefficient directeur positif :

Pour tout x de l'intervalle $I$ : $f'(x) \leq 0$

Théorème :

$\bullet$ Du sens de variation au signe de la dérivée.

Soit $f$ une fonction définie sur un intervalle $I$.

- Si $f$ est croissante sur $I$, alors pour tout $x$ de $I$, $f'(x) \geq 0$.

- Si $f$ est décroissante sur $I$, alors pour tout $x$ de $I$, $f'(x) \leq 0$.

- Si $f$ est dconstante sur $I$, alors pour tout $x$ de $I$, $f'(x) = 0$.

$\bullet$ Du signe de la dérivée au sens de variation.

Soit $f$ une fonction définie sur un intervalle $I$.

- Si pour tout $x$ de $I$, $f'(x) \geq 0$ alors, $f$ est croissante sur $I$.

- Si pour tout $x$ de $I$, $f'(x) \leq 0$ alors, $f$ est décroissante sur $I$.

- Si pour tout $x$ de $I$, $f'(x) = 0$ alors, $f$ est constante sur $I$.

Extrema :

$\bullet$ Lorsque la fonction dérivée $f'$ passe du signe positif au signe négatif en $x = a$, la fonction $f$ est croissante puis décroissante, elle admet un MAXIMUM en ce point.

$\bullet$ Lorsque la fonction dérivée $f'$ passe du signe négatif au signe positif en $x = a$, la fonction $f$ est décroissante puis croissante, admet un MINIMUM en ce point.

Exemples :

$f(x) \ = \ x^{ \ 2} -3x -4$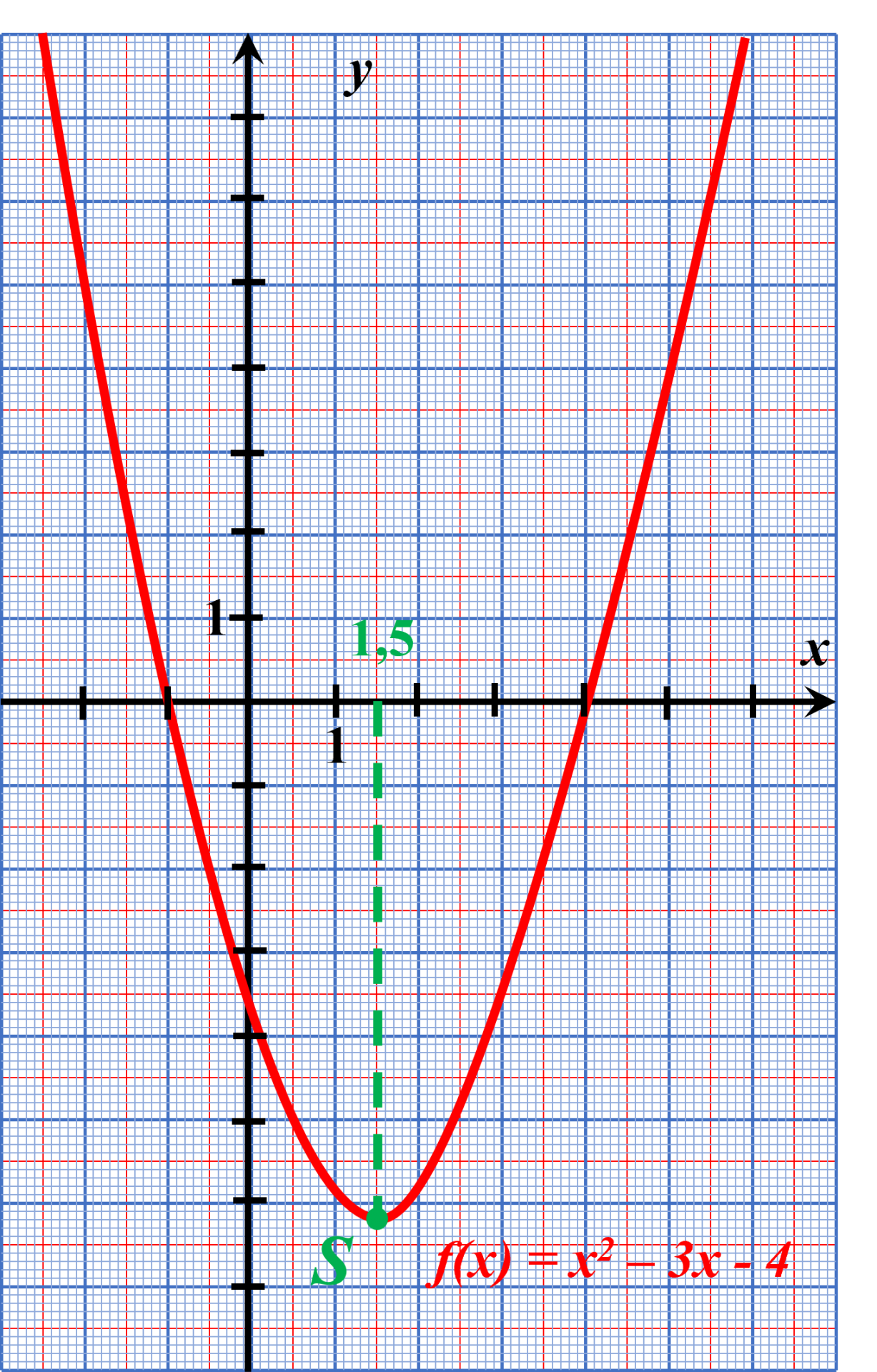

$f'(x) = 2x-3$

$x$

1,5

$f'(x)$

$f$

$f$ admet un minimum en $x = 1,5$

$f(x) \ = \ -x^{ \ 2} +3x +4$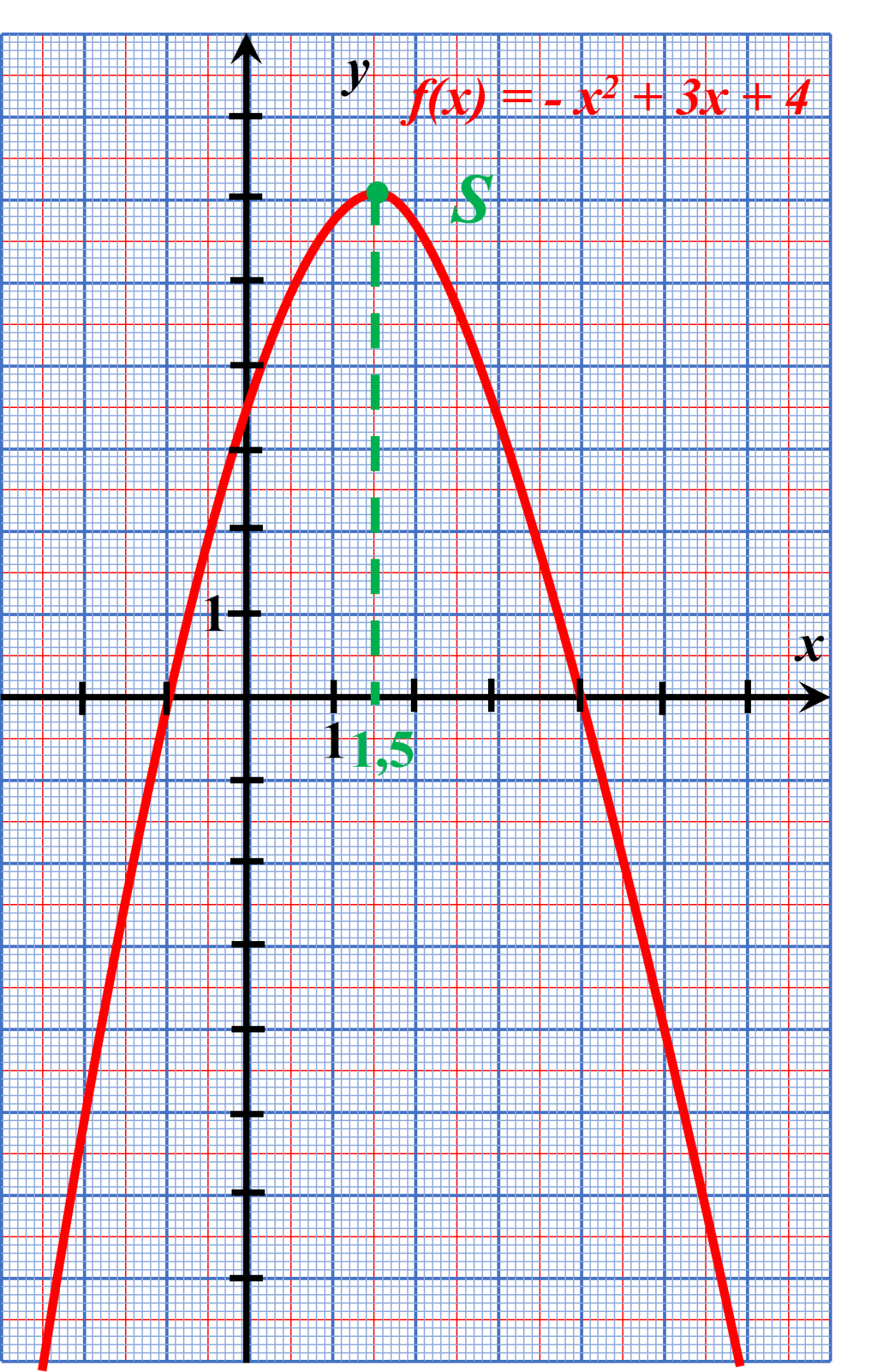

$f'(x) = -2x+3$

$x$

1,5

$f'(x)$

$f$

$f$ admet un maximum en $x = 1,5$

C4. Calculer la fonction dérivée.

C41. Dérivées des fonctions de références.

	$f(x)$	$f'(x)$	Intervalle $I$
Fonction constante	$k$	$0$	$\left ] - \infty ; + \infty \right [$
Fonction affine	$ax+b$	$a$	$\left ] - \infty ; + \infty \right [$
Fonction carré	$x^2$	$2x$	$\left ] - \infty ; + \infty \right [$
Fonction cube	$x^3$	$3 \times x^2$	$\left ] - \infty ; + \infty \right [$
Fonction puissance	$x^n$	$n \times x^{\ n-1}$	$\left ] - \infty ; + \infty \right [$
Fonction inverse	$\dfrac{1}{x}$	$- \dfrac{1}{x^2}$	$\left ] - \infty ; 0 \right [ \cup \left ] 0 ; + \infty \right [$
Fonction racine carrée	$\sqrt x$	$\dfrac{1}{2 \times \sqrt x}$	$\left ] 0 ; + \infty \right [$