Electricité

ACTIVITES

A1.Vitesse des électrons dans le cuivre.

Dès que l'on ferme l'interrupteur d'une lampe, le mouvement des électrons libres s'oriente dans la même direction et dans le même sens, dans tout le circuit. La lampe s'allume alors quasi instantanément. À quelle vitesse se déplacent les électrons ?

Fil

Document 1 : Débit et intensité électrique.

Le débit de charges électriques correspond à la quantité de charges électriques qui passent par une section d'un circuit électrique par unité de temps.

$\color{red}{\LARGE I \ = \ \dfrac{Q}{\Delta \ t}}$

I : intensité du courant en Ampères (A)

Q : quantité de charges en Coulombs (C)

$\Delta \ t$ : durée en secondes (s)

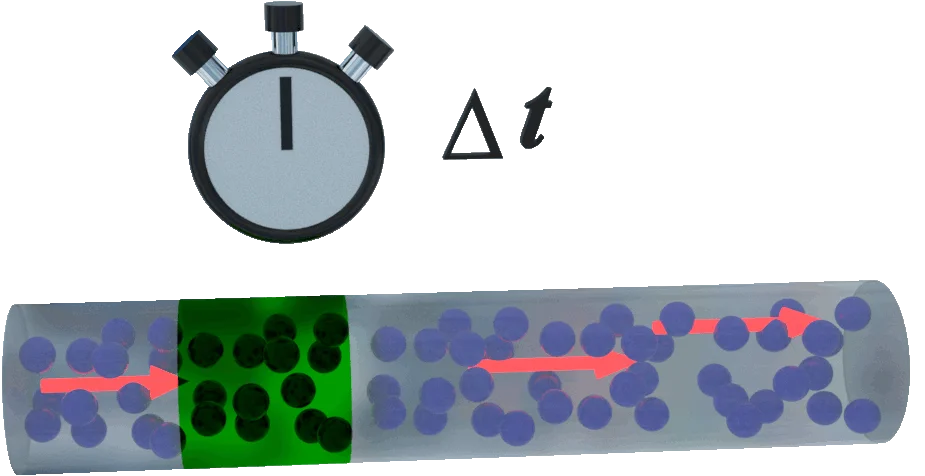
Document 2 : Débit et vitesse.

Fil

On admet que le nombre de particules qui traversent la section du fil pendant la durée $\Delta \ t = \ t_{\ 2} \ - \ t_{ \ 1}$ est contenu dans un cylindre de volume $V$ tel que :

$\color{red}{\LARGE V \ = \Delta \ t = \pi.r^{ \ 2}.v. \Delta \ t}$

$V$ : volume en $m^{ \ 3}$

$r$ : rayon du fil en $m$

$v$ :vitesse de déplacement des particules en $m.s^{ \ 1}$

$\Delta \ t $ : durée en $s$

Données :

Constante d'Avogadro : $\cal{N}_a \ = \ 6,02.10^{ \ 23} \ mol^{ \ -1}$

Charge élémentaire : $e \ = \ 1,602.10^{ \ -19} \ C$

Masse molaire atomique du cuivre : $M \ = \ 63,5 \ g.mol^{ \ -1}$

Masse volumique du cuivre : $\rho \ = \ 8,96.10^{ \ 3} \ kg.m^{ \ -3}$

Nombre d’électron libre par atome de cuivre : $1$

1.En utilisant les données, calculez le nombre N d'électrons libres contenus dans $1 \ m^{ \ 3}$ de cuivre.

2a.Donner l'expression de la charge Q contenue dans un volume V en fonction de N et V.

2b.À l'aide du document 2, en déduire une relation entre cette charge $Q$, la vitesse $v$ des électrons et la durée $\Delta \ t$ dans le cas d'un fil de cuivre de $0,50 \ mm$ de diamètre.

2c.Proposer une autre expression de la charge $Q$ traversant une section du fil pendant une durée $\Delta \ t$ , en fonction de $I$ et $\Delta \ t$.

2d.À partir des réponses données aux questions précédentes, en déduire une expression de la vitesse des charges dans le fil de cuivre. Calculez sa valeur pour une intensité du courant électrique de $100 \ mA$.

A2. Caractéristique d’une pile.

Une pile est une source de tension très utilisée.

Quel est son comportement lorsque l’intensité demandée par le circuit est importante ?

Doc1 : Conducteur ohmique.

La caractéristique d'un dipôle permet de connaître le lien qui existe entre la tension à ses bornes et l'intensité du courant qui le traverse, ceci afin de prévoir son fonctionnement dans un circuit.

La caractéristique intensité tension d'un conducteur comique c'est une droite qui passe par l'origine : le dipôle suit la loi d'Ohm.

Différents résistors

La grandeur qui caractérise un conducteur ohmique (résistor) est caractérisé par sa résistance exprimée ohms ($\Omega$). Sa valeur peut être déterminée grâce à un code couleurs.

Resistor symbol

Symbolisation

Caracteristique

Caractéristique tension/intensité aux bornes d’un conducteur ohmique

La tension U aux bornes d'un résistor est proportionnelle à l'intensité $I$ du courant électrique qui le traverse.

$\LARGE U \ = \ R \ \times \ I$

U en volts (V)

I en ampères (A)

R en Ohms ($\Omega$)

Doc2 : Le rhéostat.

Un rhéostat est une résistance réglable. Les bornes noires sont branchées aux 2 extrémités d'un enroulement de fils point la borne rouge est branchée sur un curseur qui est en contact avec le dessus de l'enroulement.

Le déplacement du curseur permet de changer la longueur du fil parcouru par le courant et donc la résistance de celui-ci.

Rheostat symbole

Symbolisation

Doc 3 : La pile, source de tension.

$\bullet$ La pile est un générateur de tension continue.

$\bullet$ La tension aux bornes d’une source idéale de tension reste constante quelle que soit l’intensité du courant qui la traverse.


Symbolisation	Caractéristique

A21. Analyse

Protocole : dessiner un montage symbolique permettant de mesurer la tension à ses bornes et l’intensité du courant qui le traverse en utilisant un rhéostat.

A22. Réalisation.

Une fois le montage réalisé et validé, mettre en œuvre le protocole en présentant vos mesures de façon adaptée.

A33. Conclusion..

Un générateur de tension continue est caractérisé par sa force électromotrice $E$ et sa résistance interne $r$.

Déterminer la caractéristique de la tension aux bornes du générateur de tension continue. En déduire les deux grandeurs qui le caractérisent dans votre étude.

A3. Chauffage par effet Joule.

Un thermoplongeur est un dispositif permettant de chauffer les liquides.

Il est constitué d'un matériau résistif qui s'échauffe lorsqu'il est parcouru par un courant électrique. C'est l'effet joule

Doc 1 : Matériel à disposition.

$\bullet$ Un calorimètre.

$\bullet$ Deux multimètres.

$\bullet$ Une éprouvette de 250 mL.

$\bullet$ Un générateur de tension continue.

$\bullet$ Trois résistances immergeables.

$\bullet$ Un thermomètre.

$\bullet$ Un chronomètre.

$\bullet$ Des fils de connexion.

$\bullet$ Un calorimètre est un récipient permettant d’isoler thermiquement son contenu de l’extérieur. Il peut cependant y avoir des échanges entre les différents corps placés à l’intérieur et l’extérieur.

$\bullet$ Un corps de masse $m_1$, passant d’une température $T_1$ à une température $T_2$ sans changer d’état physique reçoit de l’énergie thermique $E$ de la part du milieu extérieur de valeur :

$\LARGE E \ = \ m \times C \times \left( T_2 - T_1 \right)$

$E$ : énergie en Joule (J)

$m$ : masse en kg

$C$ : capacité thermique massique en $J.kg^{ \ -1}.C^{ \ -1}$. Pour l’eau : 4185 J.kg^{ \ -1}.C^{ \ -1}$

$\bullet$ Puissance électrique : $\Large P \ = \ U \times I$ (P en W, U en V, I en A).

$\bullet$ Energie électrique consommée par un conducteur ohmique sur une durée $\Delta \ t$ :

$\LARGE E_{el} \ = \ P \times \Delta \ t$

$E_{el}$ : énergie en Joule (J)

$P$ : puissance en Watt (W)

$\Delta \ t $ : durée en secondes (s)

$\bullet$ Le rendement d’une source de tension est le rapport entre l'énergie utile $E_u$ utilisée la récepteur et l'énergie absorbée $E_a$ par la source de tension.

$\LARGE \rho \ = \ \dfrac{E_u}{E_a} \ = \ \dfrac{E_u}{E_a}$

$\rho$ sans unité

$E_a \ et \ E_u$ en Joules

$P_a \ et \ P_u$ en Watts

A31. Analyse.

$\bullet$ Indiquer la conversion d’énergie effectuée par le thermoplongeur.

$\bullet$ Proposer un protocole permettant de comparée l’énergie électrique fournie à une quantité d’eau selon la résistance du thermoplongeur.

A32.Réalisation, mesures.

$\bullet$ Mettre en œuvre le protocole validé pour différentes valeurs de la résistance utilisée.

A33.Conclusion.

$\bullet$ Donner l’expression liant l’énergie électrique fournie en fonction de l’intensité du courant électrique, de la valeur de la résistance utilisée, de la tension fournie et de la durée.

$\bullet$ Comparer les résultats attendus au mesures effectuées.

EXERCICES P 257 à 266 :

11 ; 12 ; 13 ; 15 ; 17 ; 18 ; 19 ; 20 ; 23 ; 25 ; 26 ; 27 ; 29 ; 31 ; 33 ; 34 ; 37 ; 39 ; 41

COURS

C1. Le courant électrique.

C11. Les porteurs de charge.

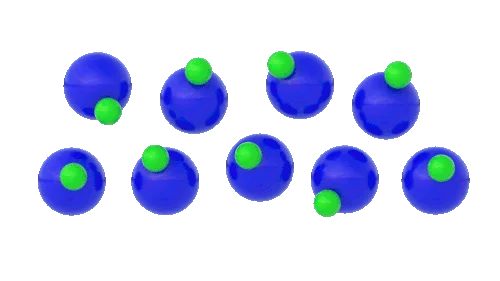
Les conducteurs portent des charges, libres de se déplacer.

Ce sont des électrons libres dans les métaux, les ions dans les solutions.

Ce sont des En l’absence de contrainte, les porteurs de charge sont animés de mouvements désorientés.

C12. Mouvement des porteurs de charge dans les conducteurs.

Lorsqu'on soumet un métal ou une solution ionique à une tension électrique, les mouvements des porteurs de charges s'ordonnent :

Les charges négatives (électrons libres et anions) se dirigent vers la borne positive du générateur, tout en restant dans leurs milieux respectifs.

Les charges positives (cations) se déplacent dans la solution en direction du pôle négatif du générateur.

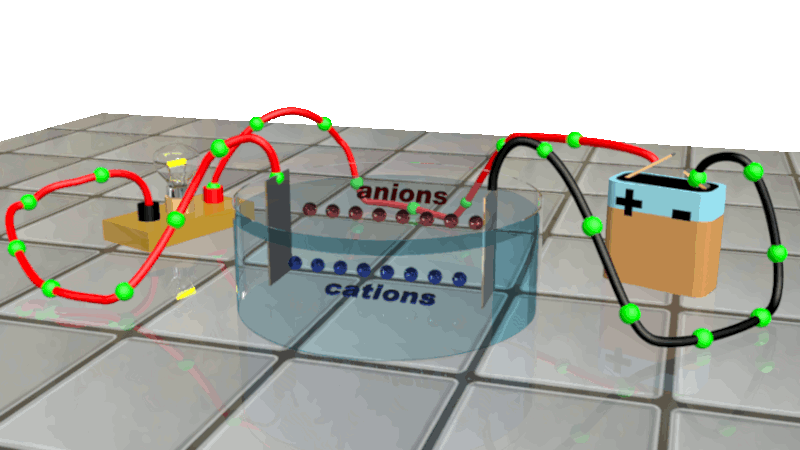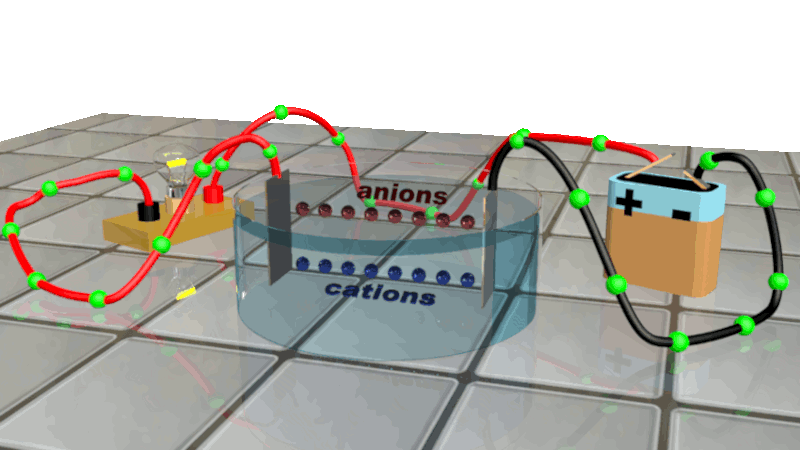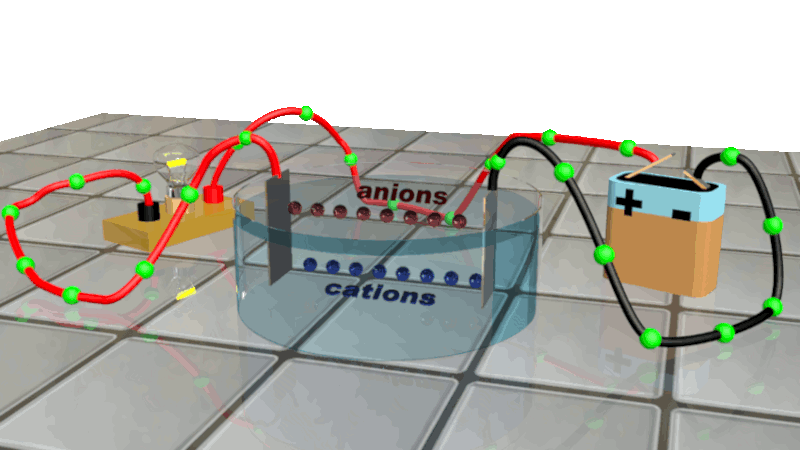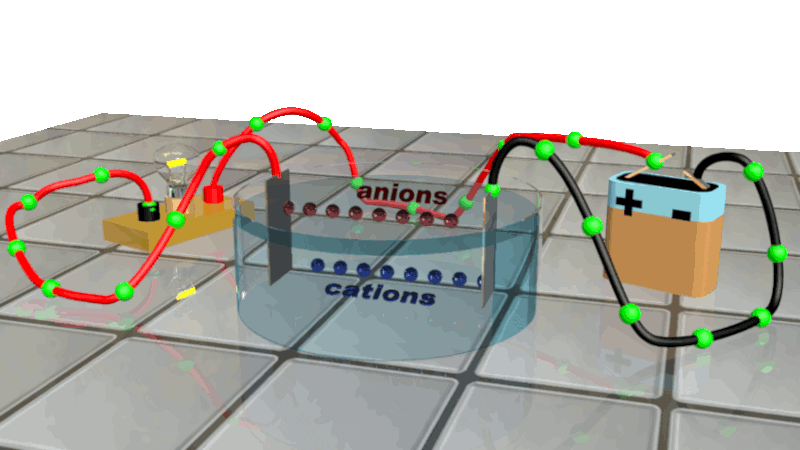
Circuit

C13. Débit de charge électrique.

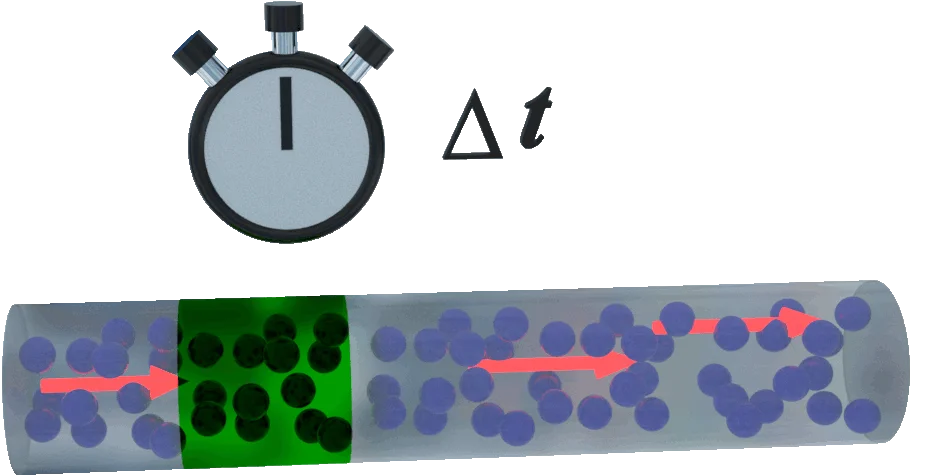
Ce débit est appelé INTENSITE DU COURANT ELECTRIQUE défini par la relation :

$\color{red}{\LARGE I \ = \ \dfrac{Q}{\Delta \ t}}$

$I$ : intensité du courant électrique (A).

$Q$ : quantié de charges électriques (C)

$\Delta \ t$ : durée (s)

C2. Source réelle de tension..

C21. Source de tension idéale.

C21a. Définition.

Une source de tension idéale fournit une tension $U_0$ constante entre ses bornes, quelque soit l'intensité du courant débité.

On la schématise de différentes sortes :

C21b. Caractéristique Intensité/tension.

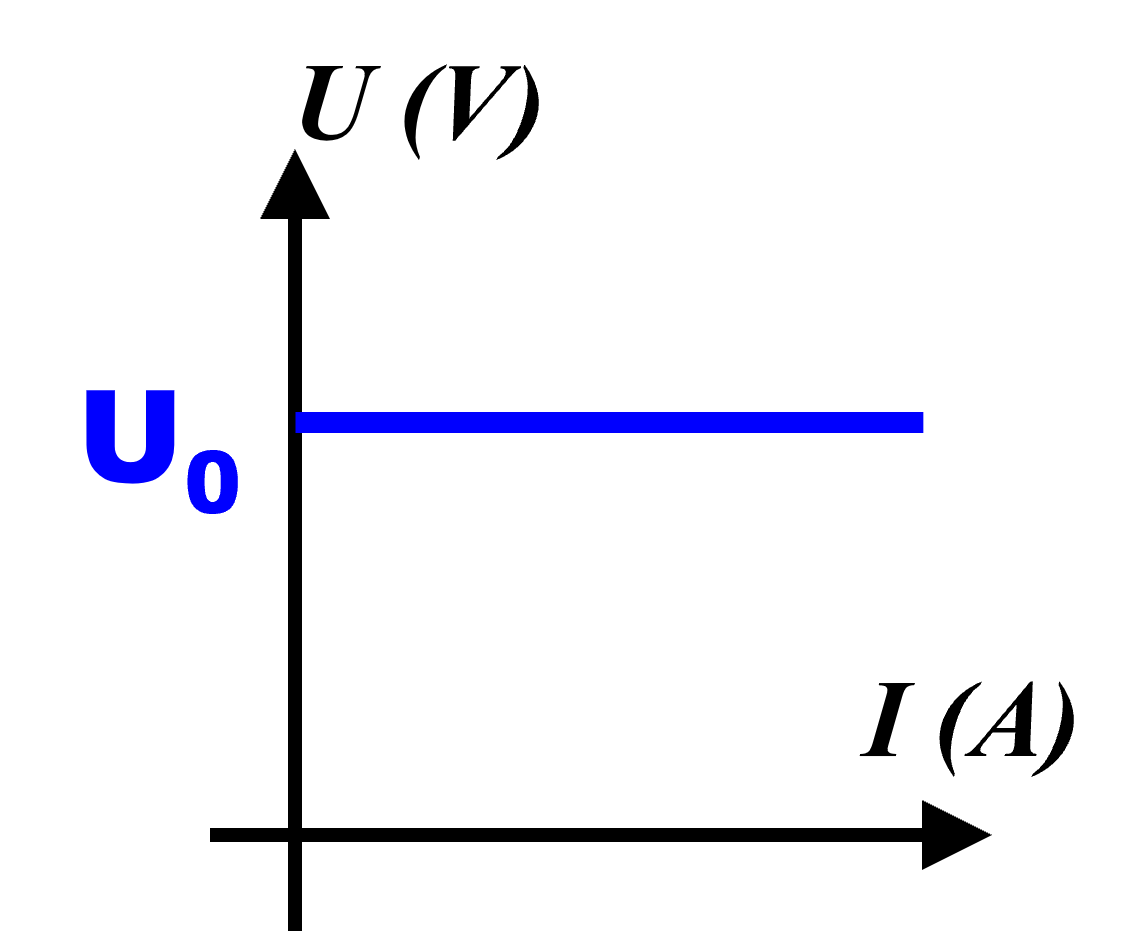
Caracteristique u0

C22. Source de tension réelle.

C22a. Définition.

Une source réelle de tension peut être modélisée par le montage en série d'une source de tension idéale et d'un résistor :

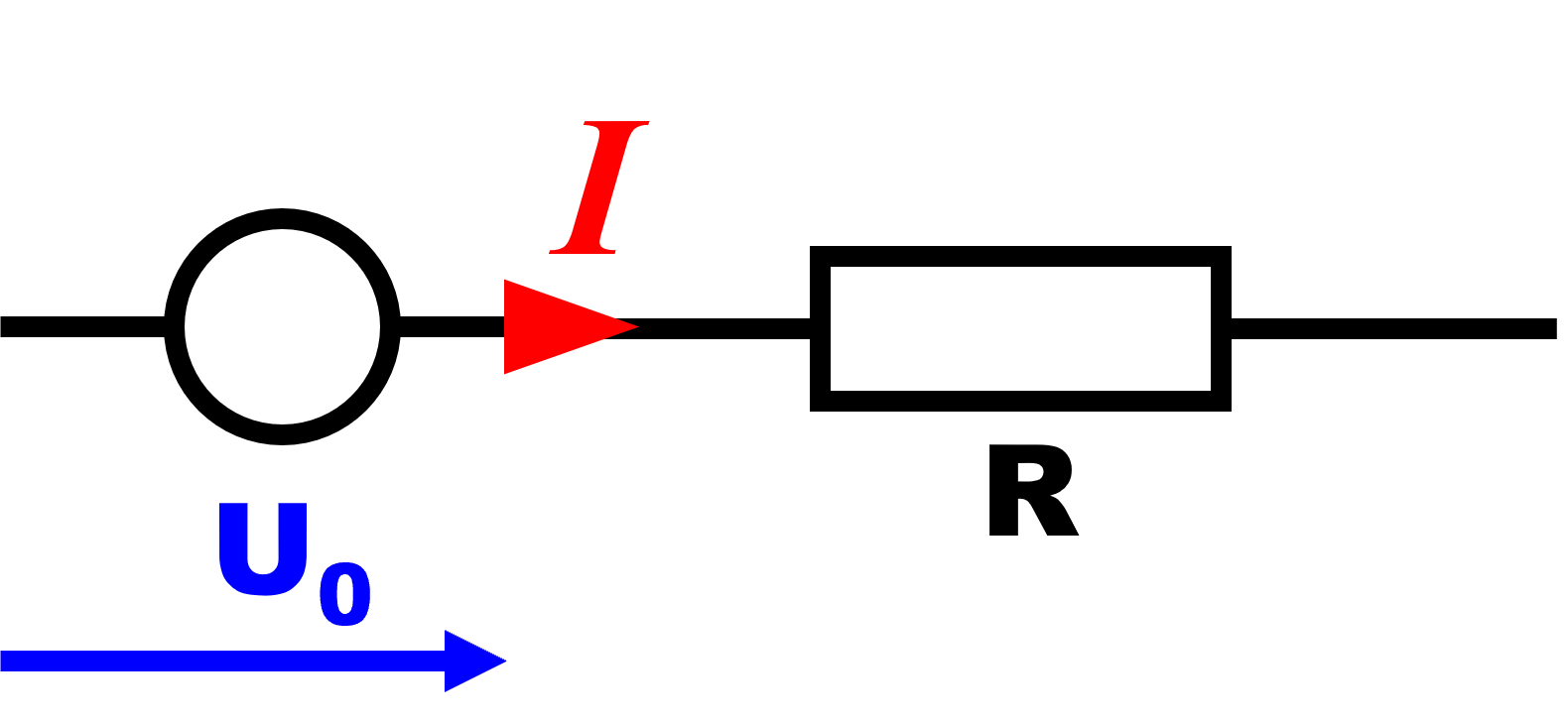La tension de la source idéale correspond à la tension "à vide" de la source de tension réelle lorsqu'elle ne délivre aucun courant (lorsque aucun récepteur n'est branché à ses bornes).

La résistance R correspond à la résistance interne de la source de tension réelle.

C22b. Conséquences.

L'existence de la résistance interne modifie le fonctionnement de la source réelle, notamment si la source doit fournir un courant électrique important.

Lorsque l'intensité du courant augmente, la tension électrique à ses bornes diminue.

C22c. Caractéristique Intensité/tension.

Caracteristique reelle

C3. Puissance et énergie.

C31. Puissance d'un dipôle.

Une source de tension fournit de la puissance électrique à un circuit.

Cette puissance est égale à la somme des puissances des dipôles passifs (résistance, lampe, etc..) contenus dans le circuit.

L'expression de la puissance est la suivante :

$\color{red}{\LARGE P \ = \ U \times I}$

$P$ : puissance utilisée par le dipôle (en W)

$U$ : tension aux bornes du dipôle (en V)

$I$ : intensité du courant électrique qui traverse le dipôle (en A)

Exemples :

Puissances électriques de dispositifs courants
Ampoule	Ordinateur	Micro-ondes	Machine à laver	Voiture électrique	Réacteur de centrale nucléaire
10 W	80 W	1 à 1,5 kW	2 kW	50 à 400 kW	1 à 1,5 kW

C32. Cas des conducteurs ohmiques.

Si on associe la définition de la puissance $\left( P = U \times I \right)$ et la loi d'Ohm $\left( U = R \times I \right)$, on trouve la relation :

$color{red}{\LARGE P = R \times I^{ \ 2}$

$P$ : puissance utilisée par le dipôle (en W)

$R$ : résistance électrique du dipôle (en \Omega$)

$I$ : intensité du courant électrique qui traverse le dipôle (en A)

Cette puissance est dissipée sous forme de chaleur. C'est ce qu'on appelle l'effet joule.

Exemples :

$\bullet$ Même les fils de connexion qu'une résistance bien qu'elle soit faible point ainsi virgule tout circuit électrique p produit de la chaleur, lors de son fonctionnement, par effet Joule.

$\bullet$ Les armoires utilisées dans les centres de données comportent de nombreux ventilateurs afin de dissiper la chaleur produite par le fonctionnement des circuits.

Centrale donnees

$\bullet$ Dans une source de tension réelle la résistance interne va dissiper de la puissance par effet joule.

C33. Energie.

Si un dispositif électrique de puissance $P$ est utilisé pendant une durée $\Delta \ t$, alors l'énergie utilisée fournie par ce dispositif est la suivante :

$\color{red}{\LARGE E \ = \ P \times \Delta \ t}$

$P$ : puissance utilisée par le dipôle (en W)

$\Delta \ t$ : durée d'utilisation (en s)

$E$ : énergie utilisée ou fournie par le dipôle (en J)

NB :