Vecteurs du plan
VECTEURS DU PLAN
A1. Randonnée.
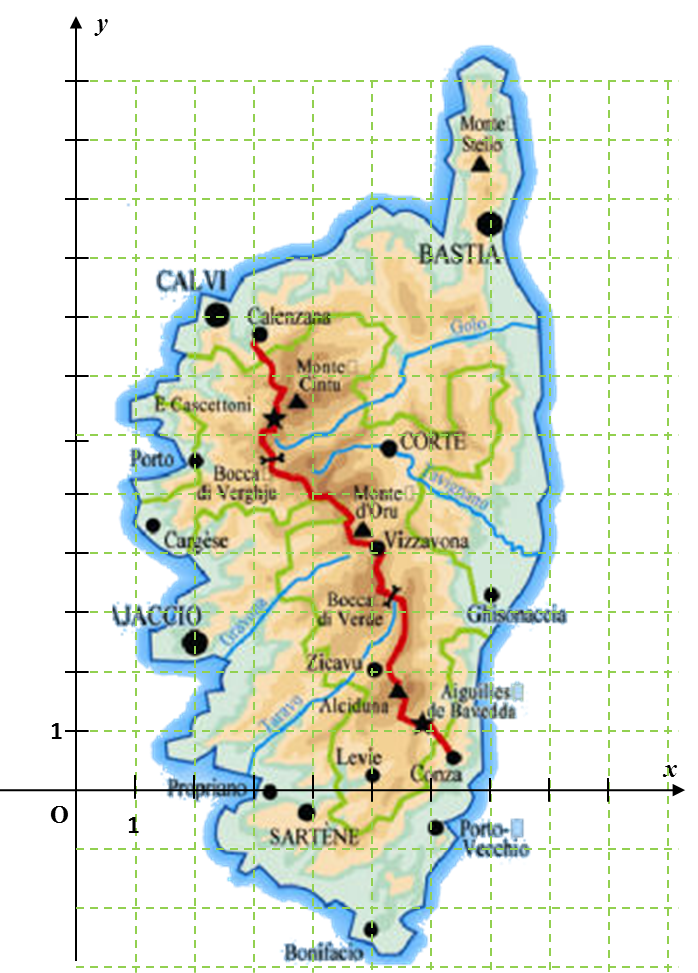 |
Gérard Marchant décide d’effectuer la partie Nord du GR20. Il prendra l’avion à Paris et se posera à Ajaccio. De là, il rejoindra Vizzavona par la route. Il marchera sur le GR20 jusqu’à Calenzana. Une fois à Calenzanna, il retournera prendre l’avion à Ajaccio.
1. Placer sur la carte ci-contre, les points dont on donne les coordonnées : $A \left ( 2 ; 2,5 \right ) \ \ B \left (3,2 ; 7,8 \right )$ et $C \left ( 5,1 ; 4,1 \right )$ |
2. Associer à chaque point, le lieu correspondant.
|
Lieu |
Point |
|
|
Ajaccio $\bullet$ |
$\bullet \ \ A$ |
|
|
Calenzana $\bullet$ |
$\bullet \ \ B$ |
|
|
Vizavona $\bullet$ |
$\bullet \ \ C$ |
3. Mesurer sur la carte, les distances suivantes :
$AB \ = \ ........$
$AC \ = \ ........$
$BC \ = \ ........$
4. En déduire la nature du triangle $ABC$.
....................................................................................................................................................................
....................................................................................................................................................................
5. Représenter sur la carte les déplacements du randonneur d’Ajaccio à Vizzavona, puis de Vizzavona à Calenzana et enfin de Calenzana à Ajaccio.
6. Comment se nomment ces représentations ?
....................................................................................................................................................................
7. Donner leurs notations.
8. Déduire une relation entre ces trois grandeurs.
....................................................................................................................................................................
A2. En moto.
Pour économiser de l’essence, Angelo descend en roue libre, en ligne droite.
On a pris deux clichés à des instants différents.
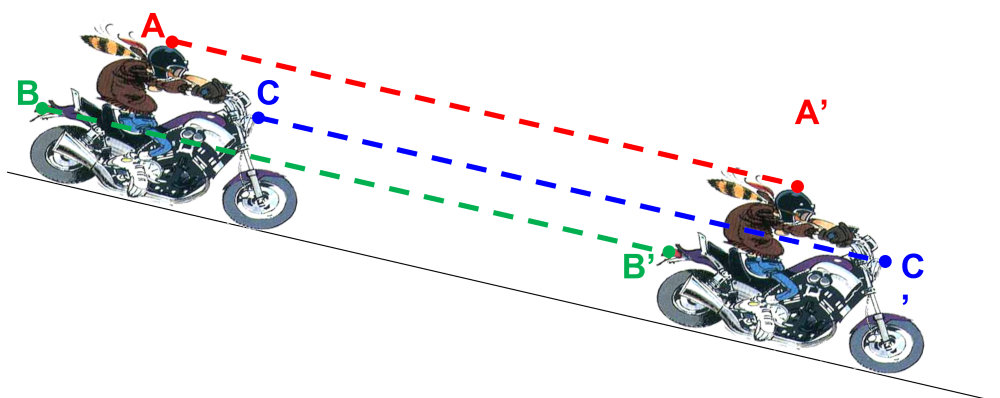
1a. Tracer au crayon les diagonales du quadrilatère $\left ( AA’B’B \right )$.
1b. Quelle conclusion en tirer quant à la nature de ce quadrilatère ?
....................................................................................................................................................................
1c. Quelle conclusion en tirer quant aux droites $\left ( AA’ \right )$ et $\left ((BB’ \right )$ ?
....................................................................................................................................................................
1d. Quelle conclusion en tirer quant aux distances $AA’$ et $BB’$ ?
....................................................................................................................................................................
2a. Tracer au crayon les diagonales du quadrilatère $\left ( AA’C’C \right )$.
2b. Quelle conclusion en tirer quant à la nature de ce quadrilatère ?
....................................................................................................................................................................
2c. Quelle conclusion en tirer quant aux droites $\left ( AA’ \right )$ et $\left ( CC’ \right )$ ?
....................................................................................................................................................................
2d. Quelle conclusion en tirer quant aux distances $AA’$ et $CC’$ ?
....................................................................................................................................................................
3a. Tracer au crayon les diagonales du quadrilatère $\left ( CC’B’B \right )$.
3b. Quelle conclusion en tirer quant à la nature de ce quadrilatère ?
....................................................................................................................................................................
3c. Quelle conclusion en tirer quant aux droites $\left ( CC’ \right )$ et $\left (BB’ \right )$ ?
....................................................................................................................................................................
3d. Quelle conclusion en tirer quant aux disatnces $CC’$ et $BB’$ ?
....................................................................................................................................................................
A3. En utilisant Geogebra.
A31. Composantes d’un vecteur.
|
$\bullet$ Tracer dans un repère, le vecteur défini par les points $A \left ( 1 \ ; \ 1 \right )$ et $B \left ( 4 \ ; \ 5 \right )$ $\bullet$ Afficher la "valeur" de ce vecteur, et recopier la notation obtenue. ...................................... $\bullet$ Que représentent les deux nombres obtenus ? ...................................... $\bullet$ Retrouver ces deux grandeurs par le calcul. ...................................... |
 |
A32. Norme d’un vecteur.
|
$\bullet$ Ajouter le point $C \left ( 4 \ ; \ 1 \right )$ $\bullet$ Tracer le segment $\left [ AC \right ]$, et afficher sa "valeur". ...................................... $\bullet$ Que représente cette valeur ? ...................................... $\bullet$ Tracer le segment $\left [ CB \right ]$, et afficher sa "valeur". ...................................... $\bullet$ Tracer le segment $\left [ AB \right ]$, et afficher sa "valeur". ...................................... $\bullet$ Trouver une relation entre ces trois "valeurs" . ...................................... |
 |
A33. Coordonnées du milieu d’un segment.
|
$\bullet$ Ajouter le milieu du segment $\left [ AB \right ]$ $\bullet$ Afficher sa "valeur". ...................................... $\bullet$ Que représentent les nombres obtenus ? ...................................... $\bullet$ Retrouver ces valeurs par le calcul. ...................................... ...................................... ...................................... |
 |
A34. Somme de vecteurs.
|
$\bullet$ Placer dans un repère, le vecteur défini par les points $A \left ( 1 \ ; \ 1 \right )$ et $B \left ( 4 \ ; \ 5 \right )$ et afficher sa"valeur". ...................................... $\bullet$ Placer dans un repère, le vecteur défini par les points $B \left ( 4 \ ; \ 5 \right )$ et $C \left ( 8 \ ; \ 7 \right )$ et afficher sa"valeur". ...................................... $\bullet$ Ajouter le vecteur défini par les points $A$ et $C$, et afficher sa "valeur". ...................................... $\bullet$ Que représente ce vecteur ? ...................................... $\bullet$ Retrouver sa "valeur" par le calcul. ...................................... ...................................... ...................................... |
 |
COURS.
C1. Eléments caractéristiques d’un vecteur.
|
 |
Dans l'exemple ci-dessus :
$\bullet$ L’origine du vecteur est : .......................
$\bullet$ L’extrémité du vecteur est : .......................
$\bullet$ La direction du vecteur est : .......................
$\bullet$ Le sens du vecteur est : .......................
$\bullet$ La norme du vecteur est : .......................
C2. Vecteurs égaux, opposés, vecteur nul.
C21. Vecteurs égaux.
|
Deux vecteurs sont égaux s’ils ont les mêmes caractéristiques : $\bullet$ Même ........................ $\bullet$ Même ........................ $\bullet$ Même ........................ |
 |
C22. Vecteurs opposés.
|
Deux vecteurs sont égaux s’ils ont les mêmes caractéristiques : $\bullet$ Même ........................ $\bullet$ Même ........................ $\bullet$ Et sont de ........................ NOTATION : L'opposé du vecteur $\overrightarrow {AB}$ est noté : ......... REMARQUE : $ - \ \overrightarrow {AB} \ = \ $............ |
 |
C23. Vecteur nul.
Un vecteur est nul si sa norme est égale à $0$.
Notation :
Le vecteur nul est noté : ..............
Remarque :
$\overrightarrow{AA} \ = \ $...........
C3. Somme de deux vecteurs.
La somme de deux vecteurs peut être construite de deux façons :
|
C31. Méthode de Chasles.
On place les vecteurs "bout-à-bout" :
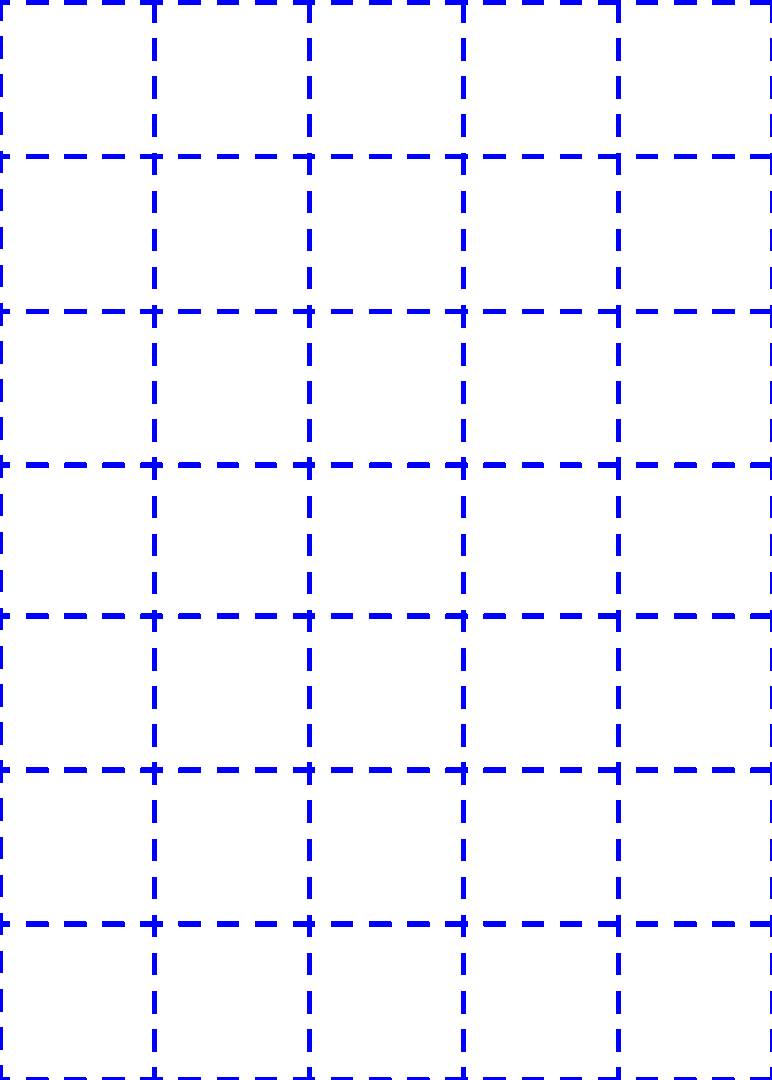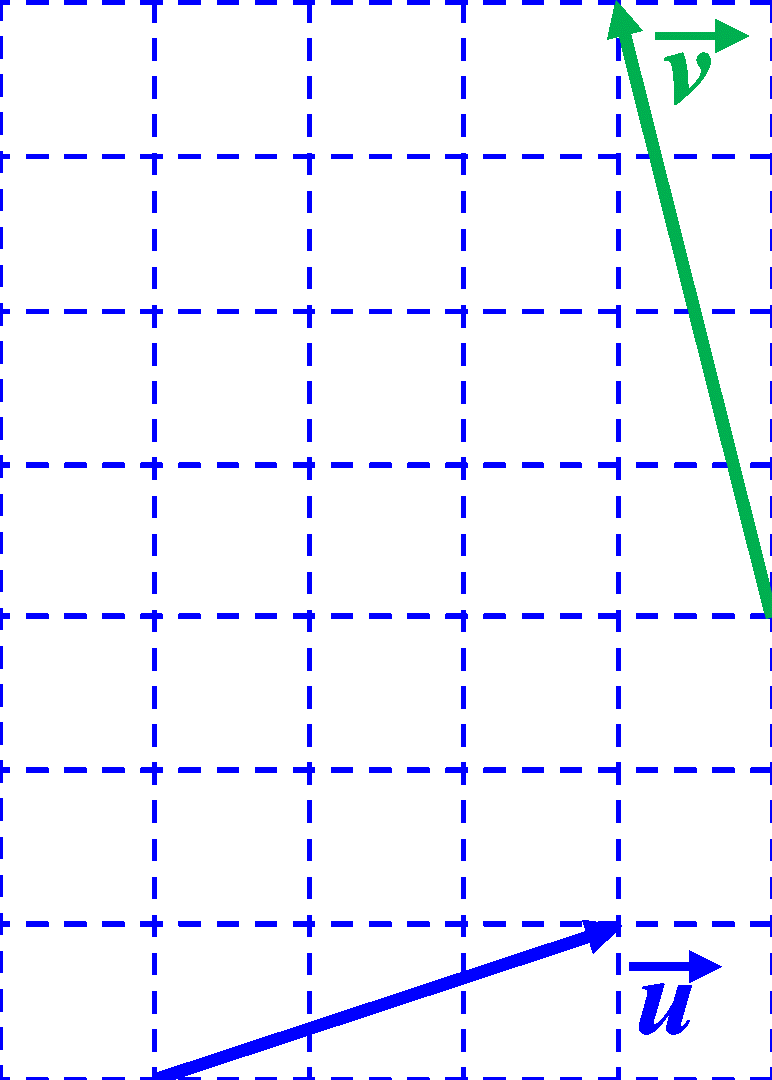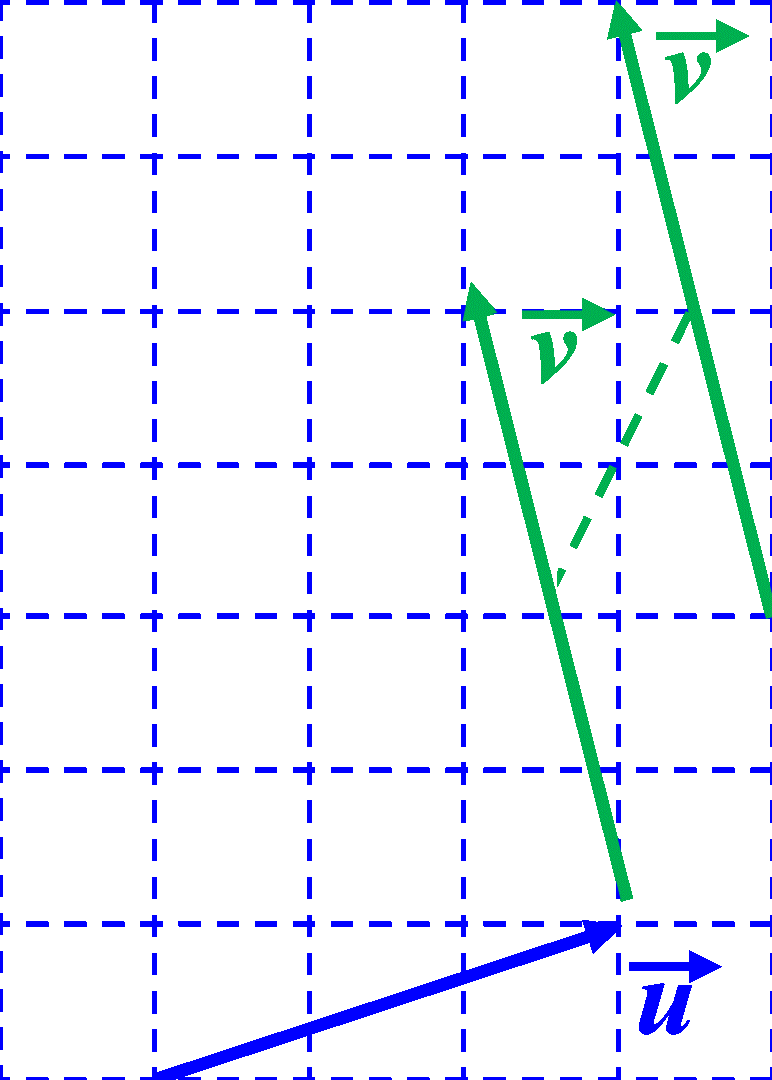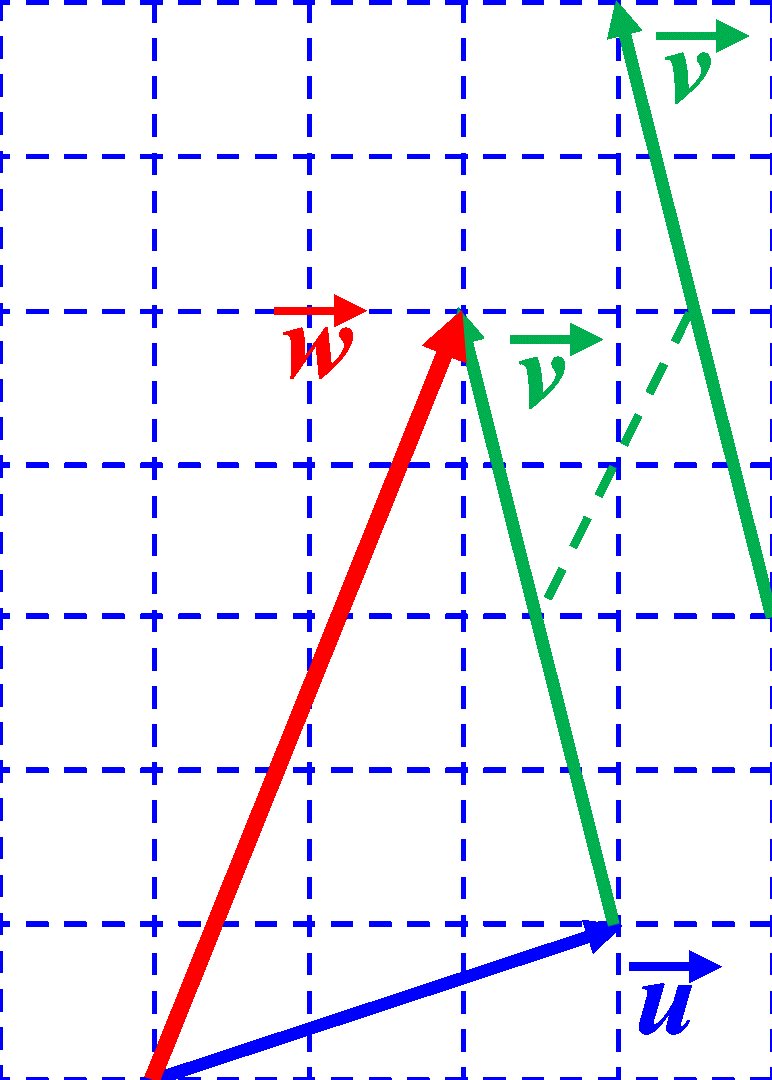
Ci-dessus, $\overrightarrow w$ est la somme de $\overrightarrow u$ et $\overrightarrow v$ On note : $\overrightarrow w \ = \ $..................... |
C32. Méthode du parallélogramme. On rapporte les deux vecteurs à la même origine. On trace la diagonale du parallélogramme ayant des côtés représentants de chaque vecteur. 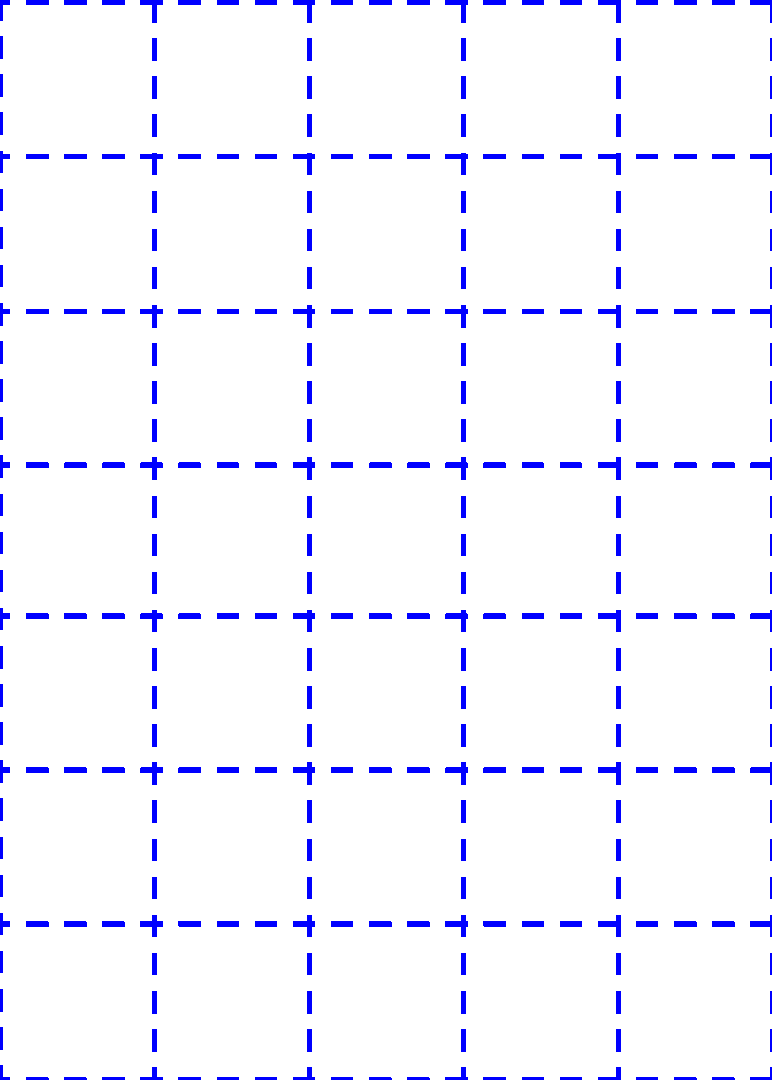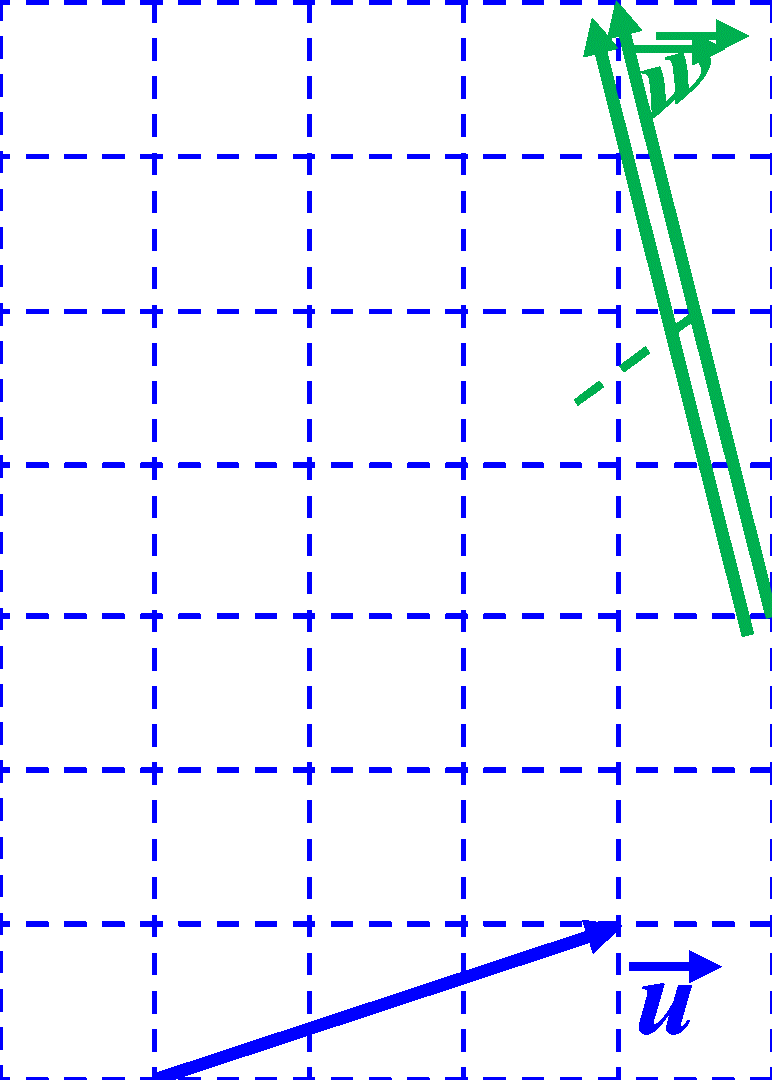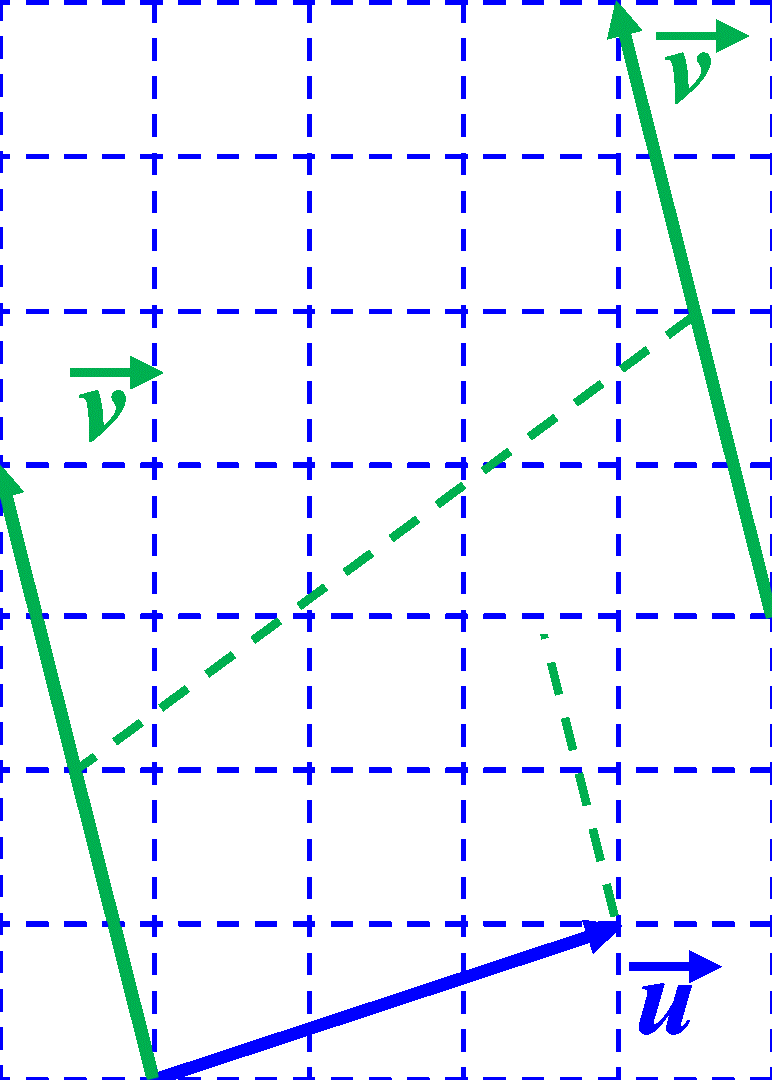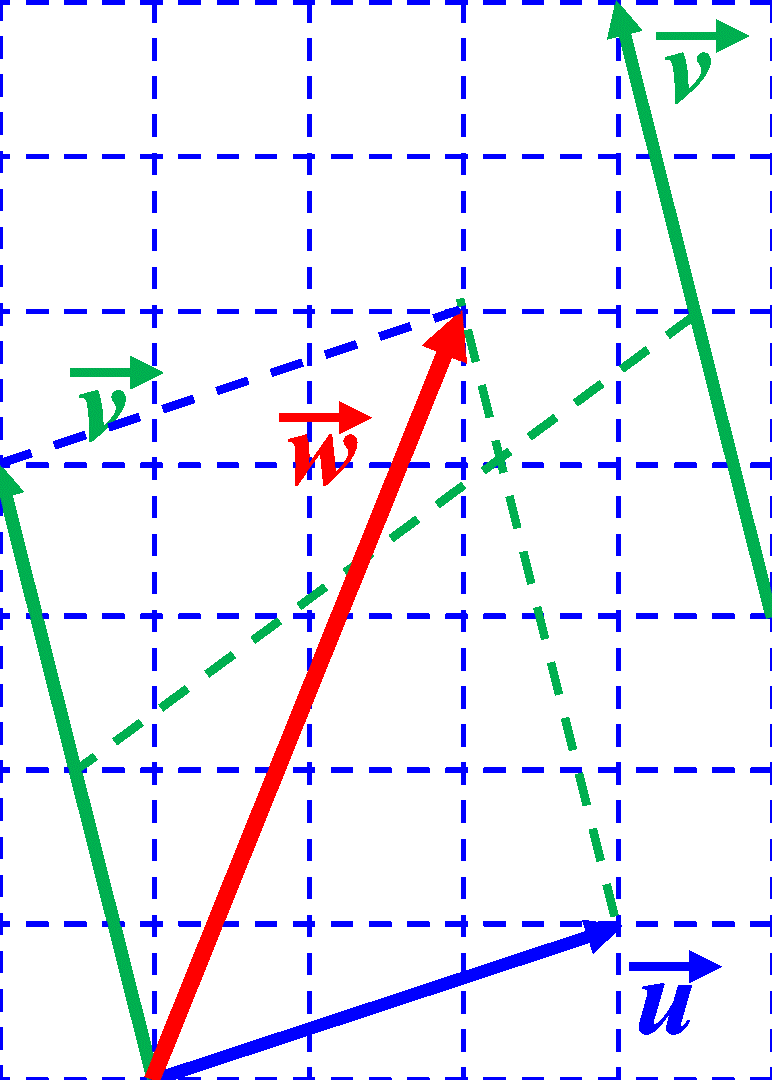
|
C33. Application.
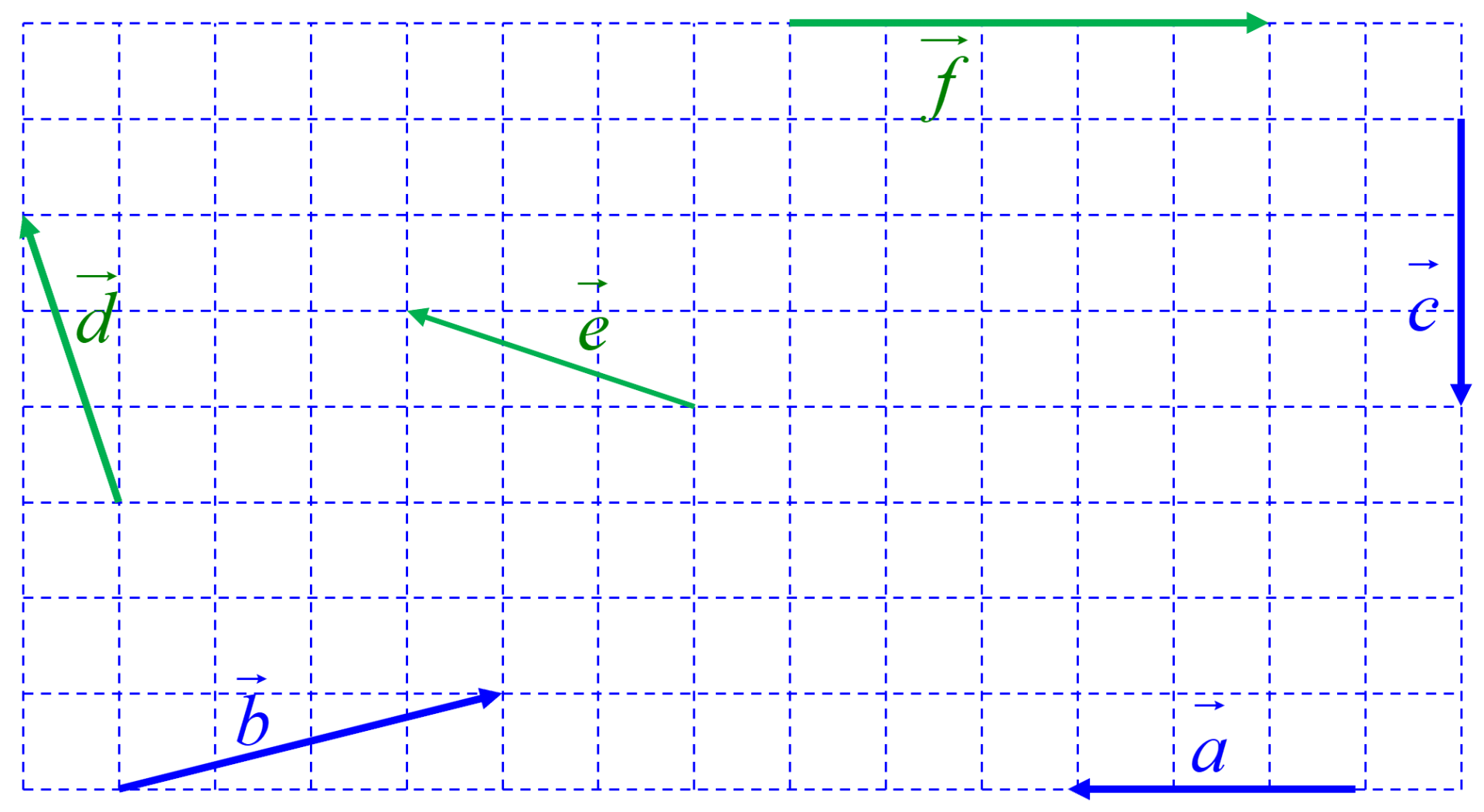 |
Tracer les vecteurs suivants : $\bullet \ \overrightarrow u \ = \ \overrightarrow a + \overrightarrow e$ $\bullet \ \overrightarrow v \ = \ \overrightarrow b + \overrightarrow d$ $\bullet \ \overrightarrow w \ = \ \overrightarrow c + \overrightarrow f$ $\bullet \ \overrightarrow t \ = \ \overrightarrow f + \overrightarrow e$ $\bullet \ \overrightarrow s \ = \ \overrightarrow c + \overrightarrow d$ |
C4. Coordonnées d’un vecteur dans le plan.
C41. Introduction.
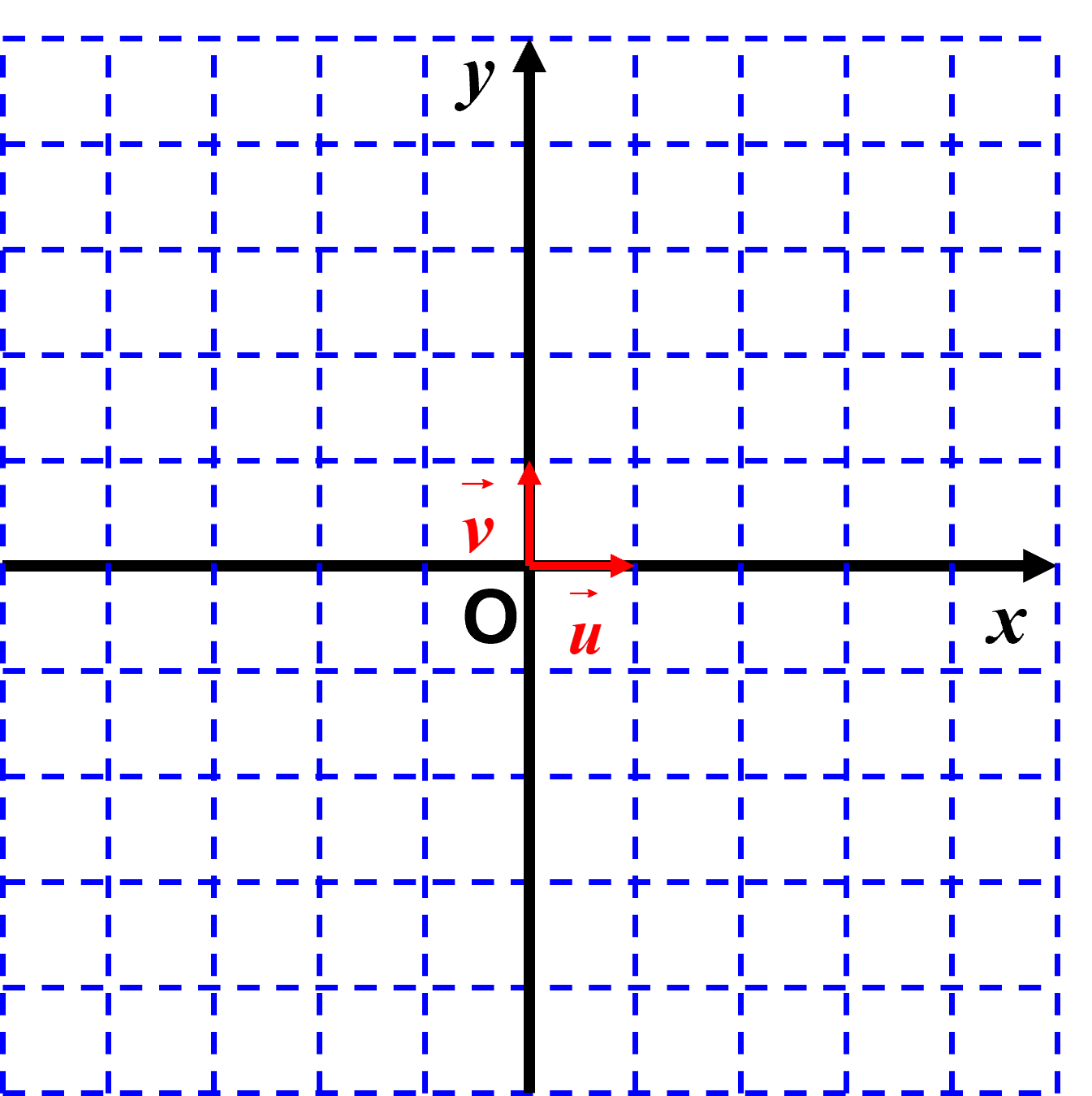
On se placera dans un repère orthonormé direct :
|
$\bullet$ L'axe des abscisses a pour origine le point $O$. $\bullet$ Il est orienté selon un vecteur $\overrightarrow u$ de norme $1$. $\bullet$ L'axe des ordonnées a pour origine le même point $O$. $\bullet$ Il est orienté selon un vecteur $\overrightarrow v$ de norme $1$. $\bullet$L'angle entre les vecteurs $\overrightarrow u$ et $\overrightarrow v$ est égal à $+ \dfrac{\pi}{2}$ : $\left (\overrightarrow u \ ; \ \overrightarrow v \right ) = \ + \ \dfrac{\pi}{2}$ |
 |
C42. Coordonnées d’un vecteur.
|
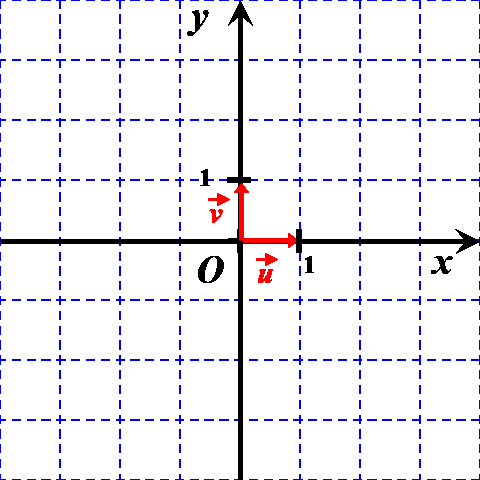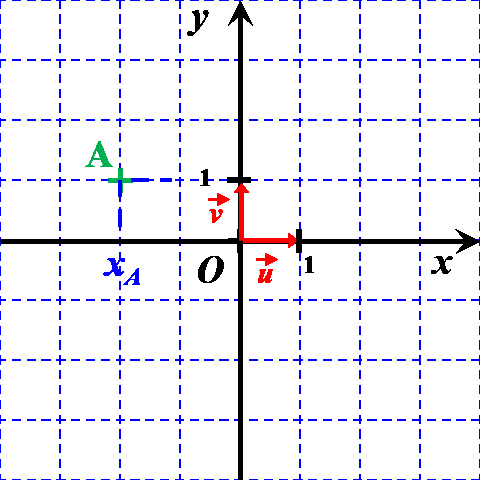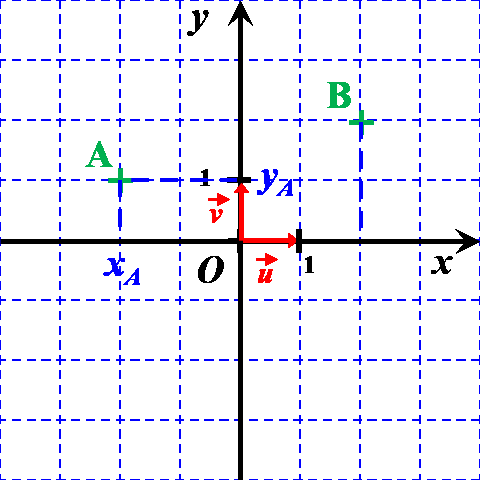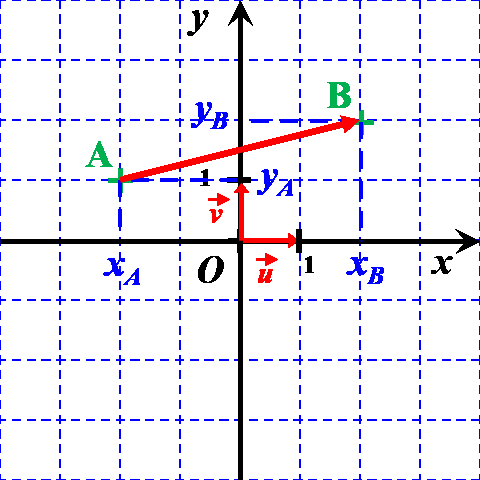
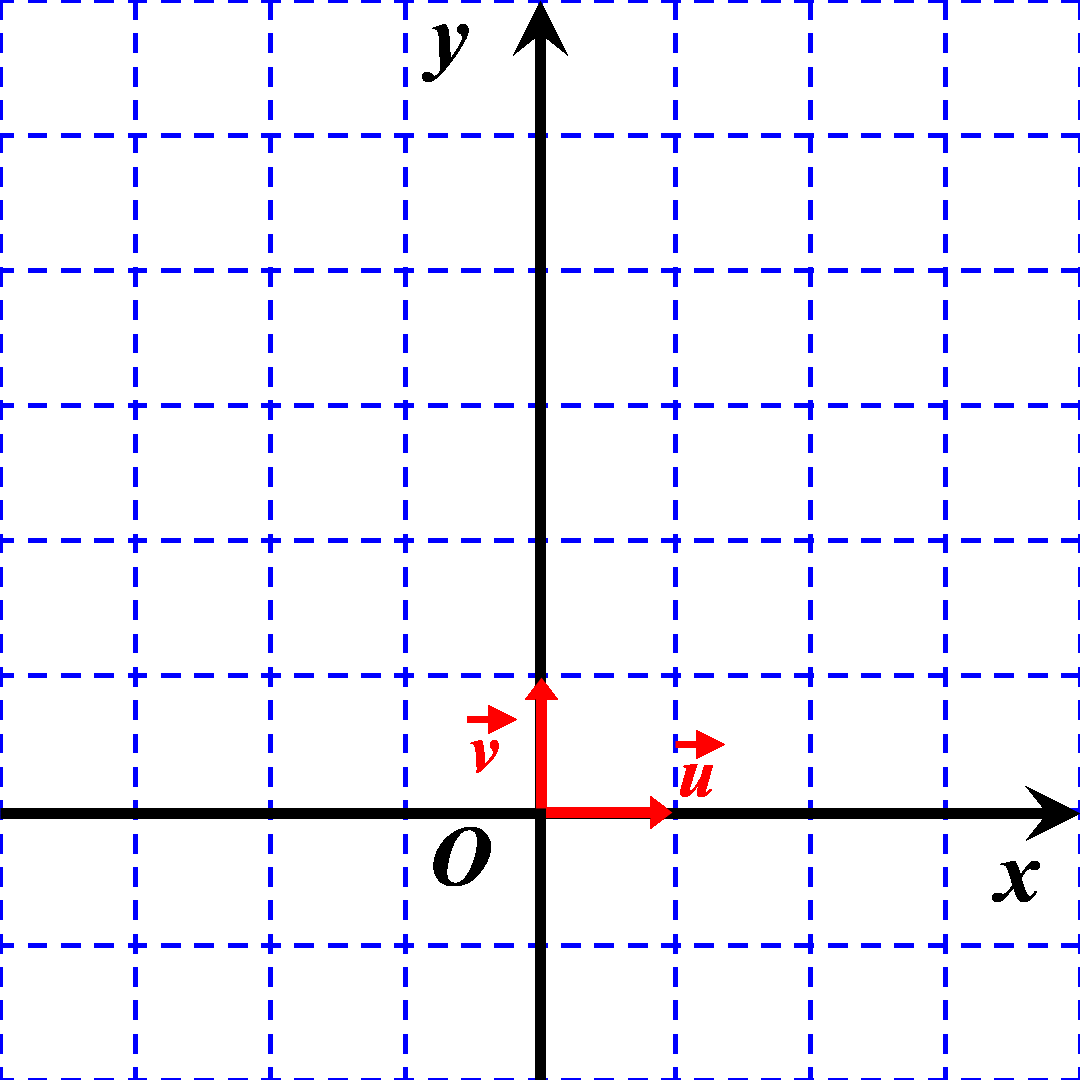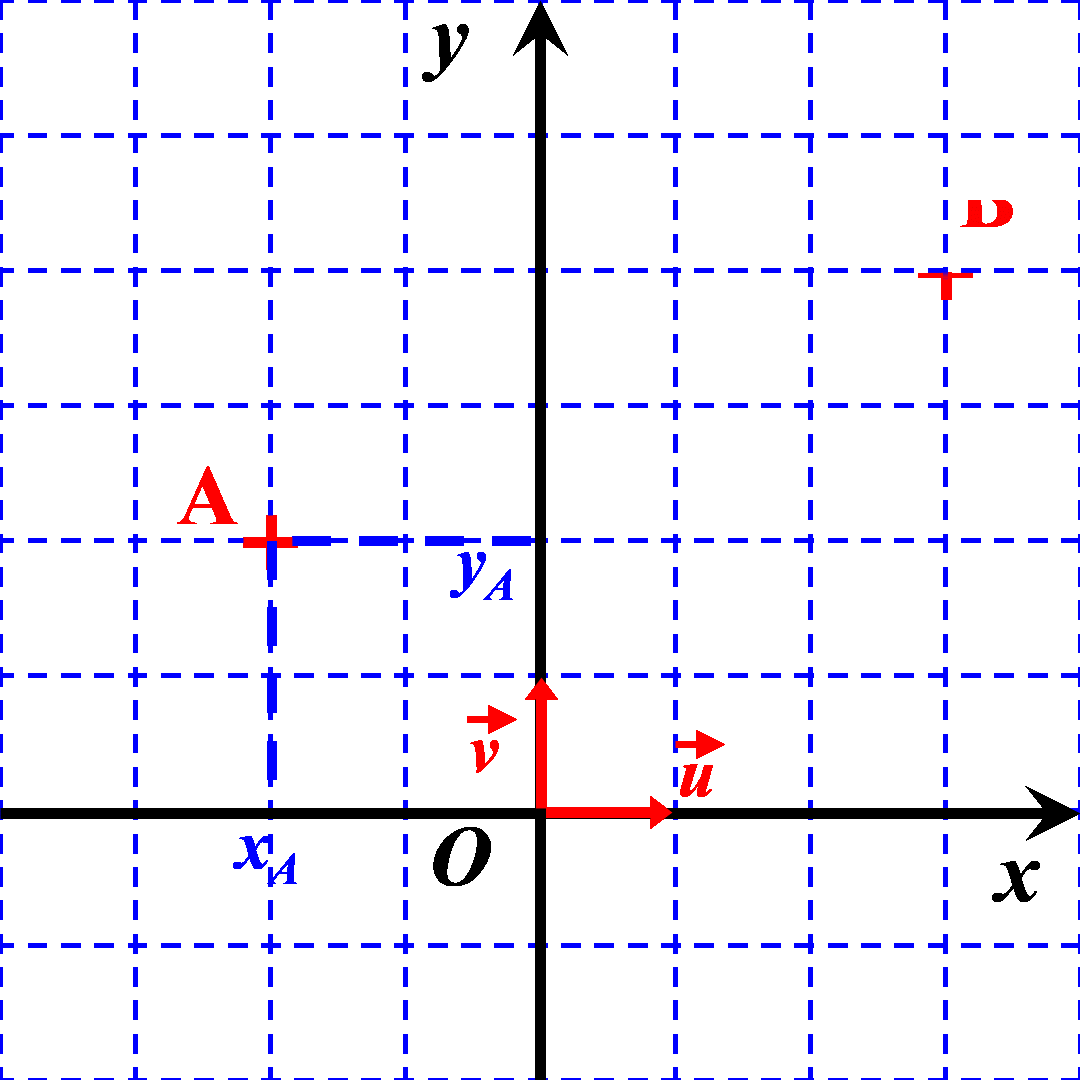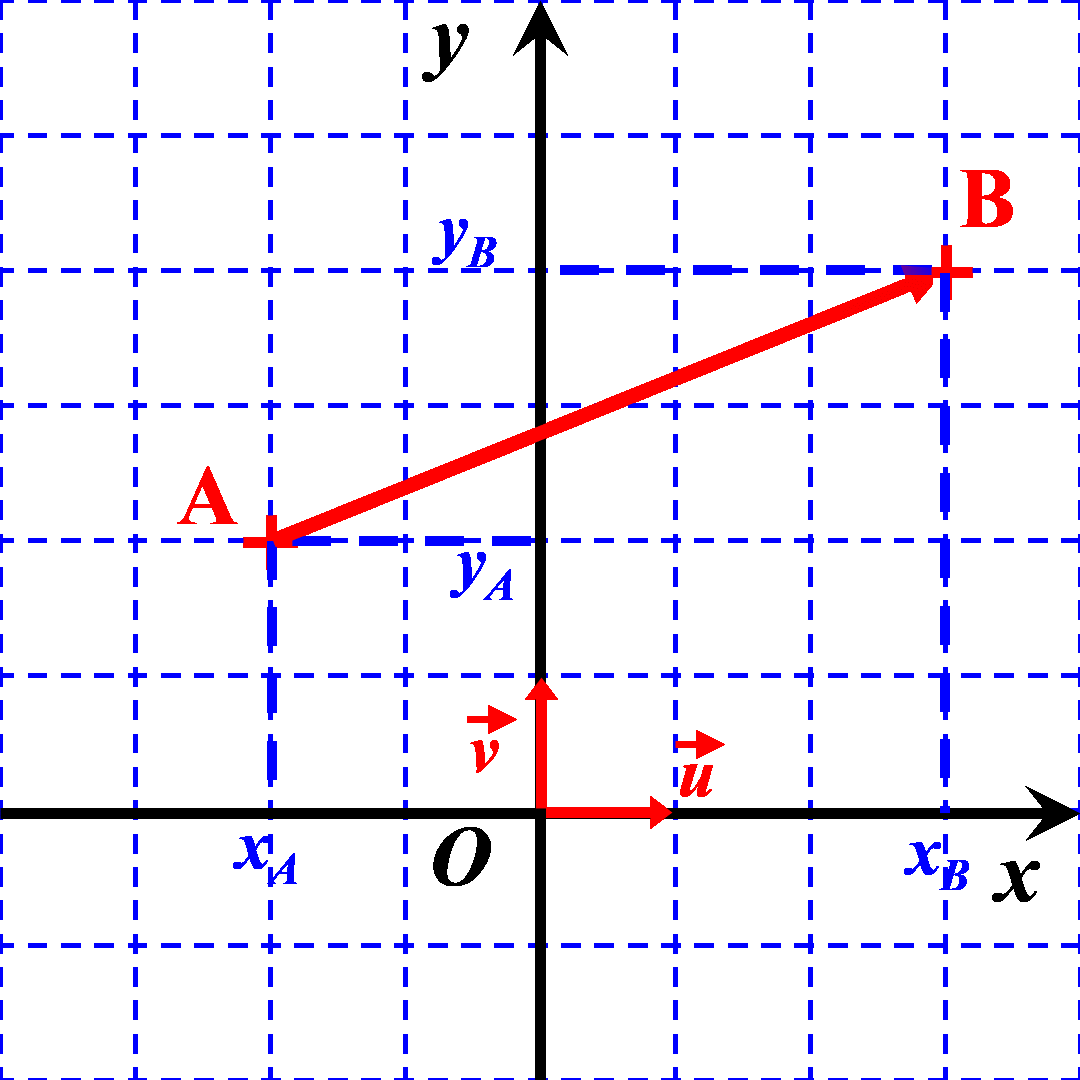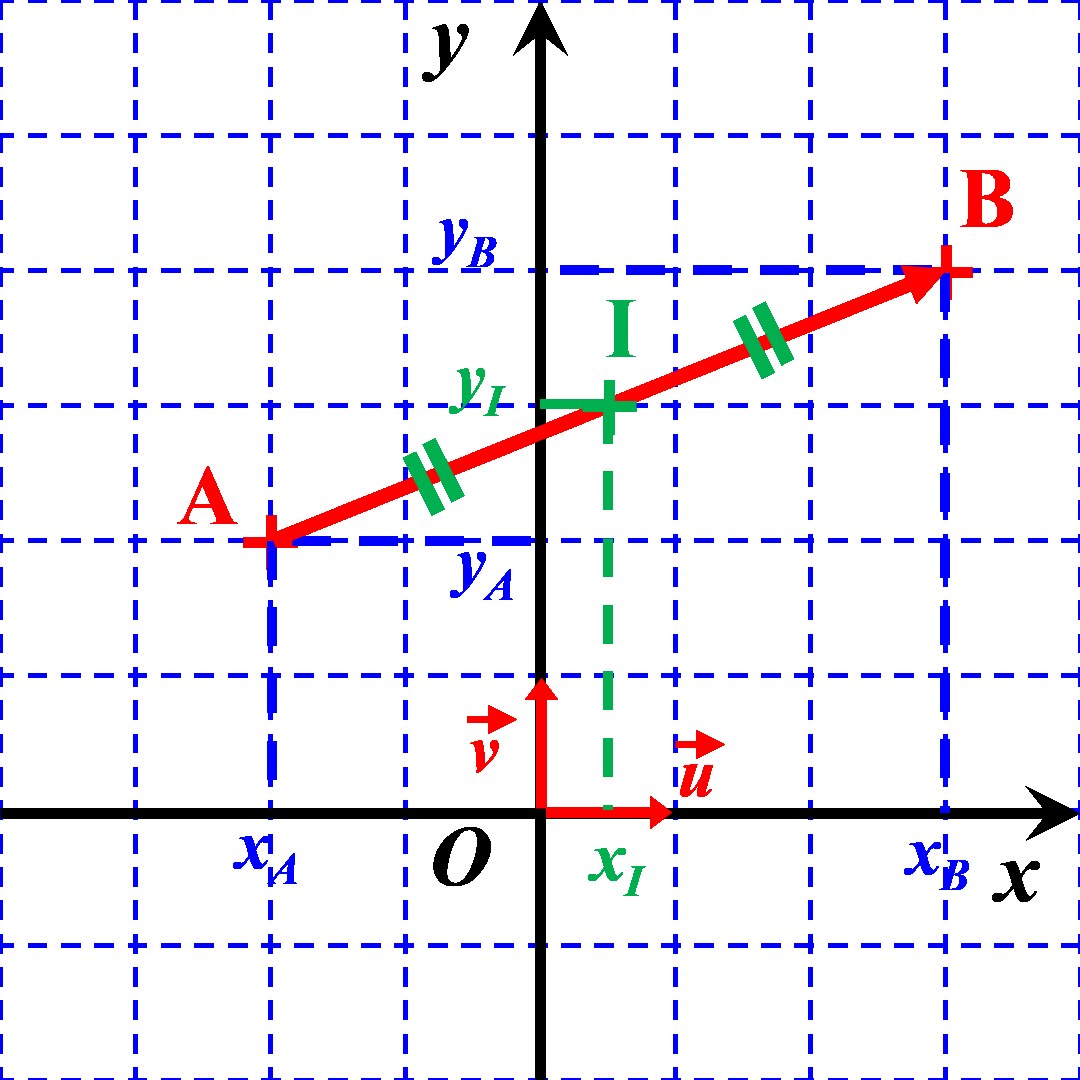
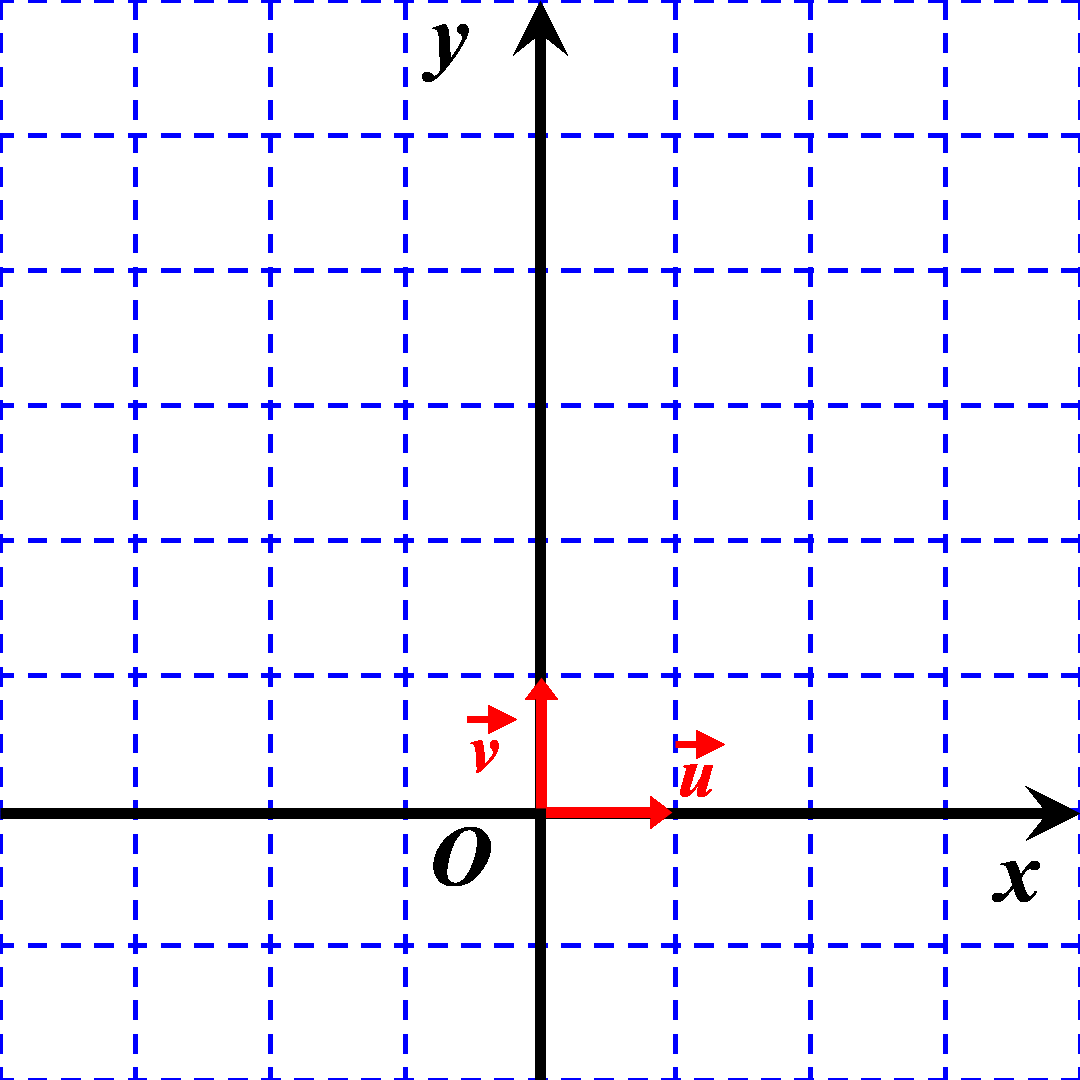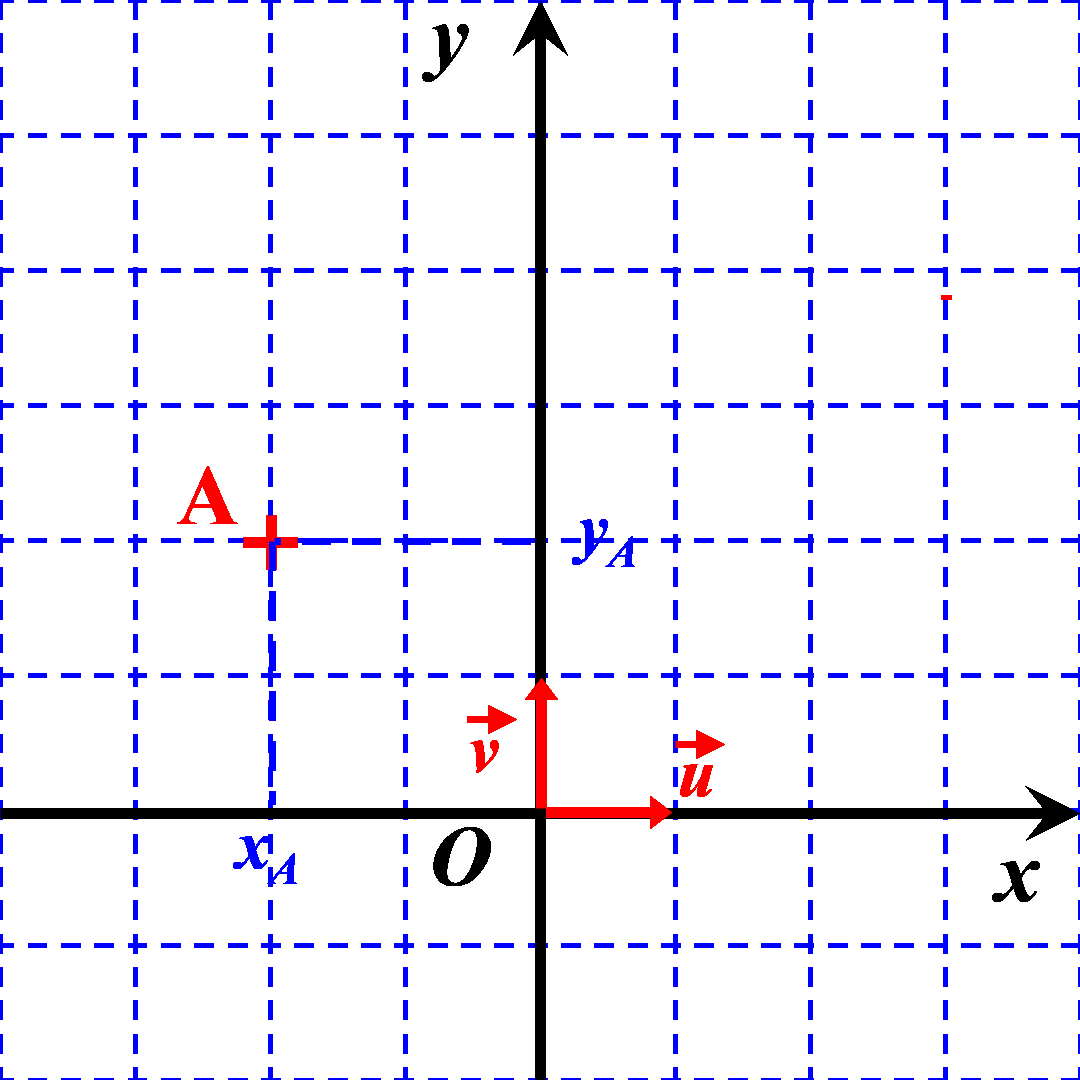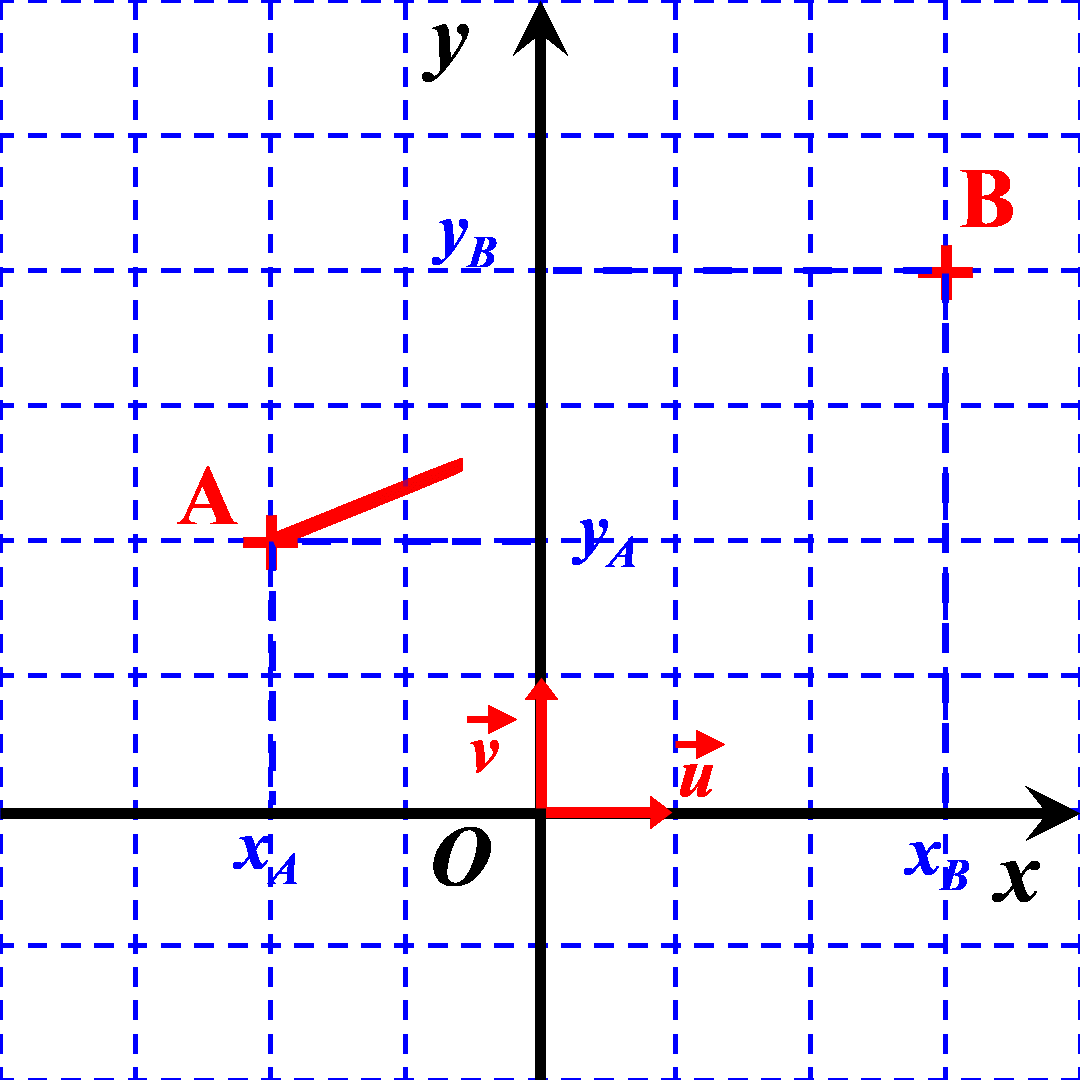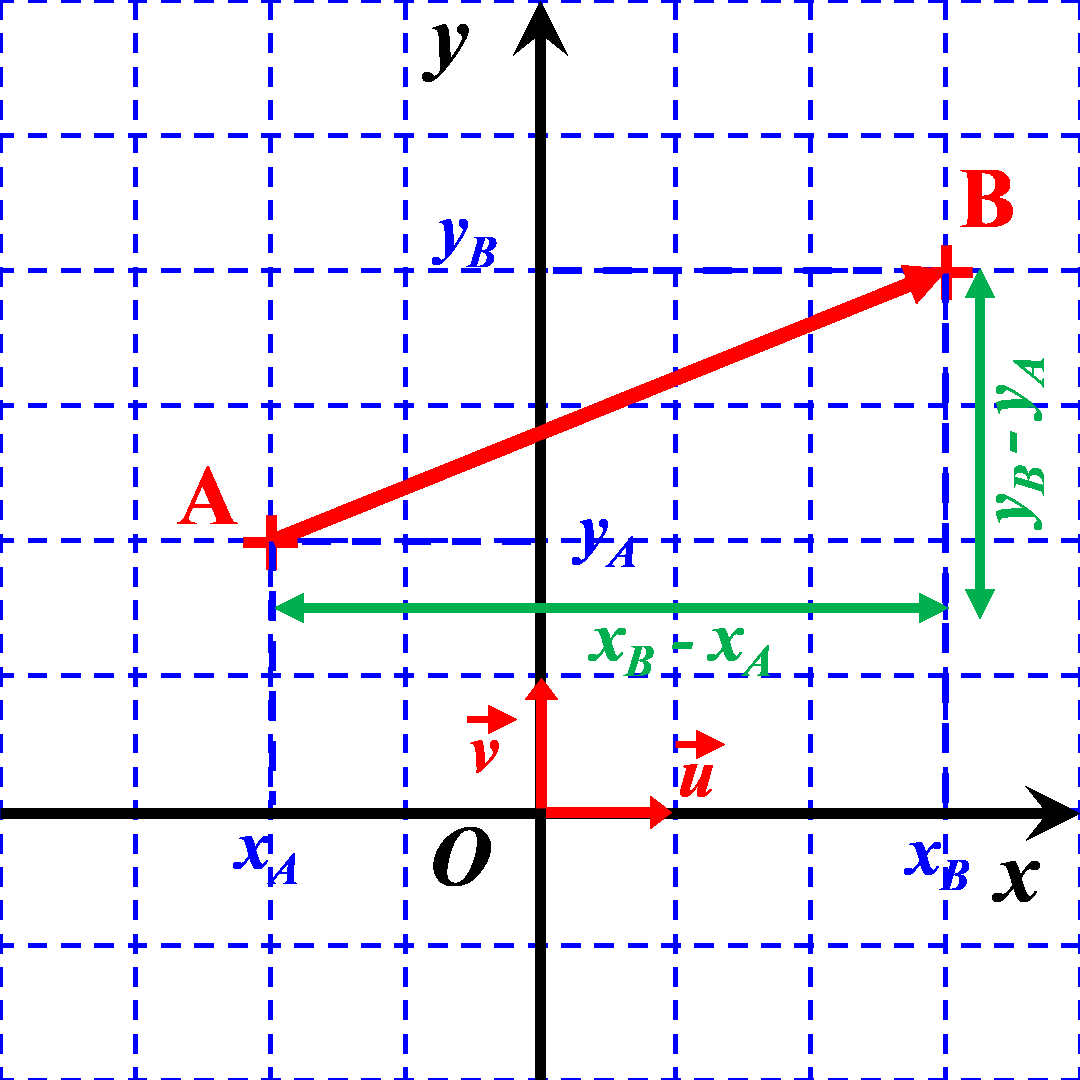
On considère deux points $A$ et $B$ du plan définis par leurs coordonnées $A \left ((x_A \ ; \ y_A \right )$ et $B \left ((x_B \ ; \ y_B \right )$.
Exemple : Déterminer les coordonnées du vecteur $\overrightarrow {AB}$ du vecteur ci-contre. ..................................... ..................................... ..................................... ..................................... |
 |
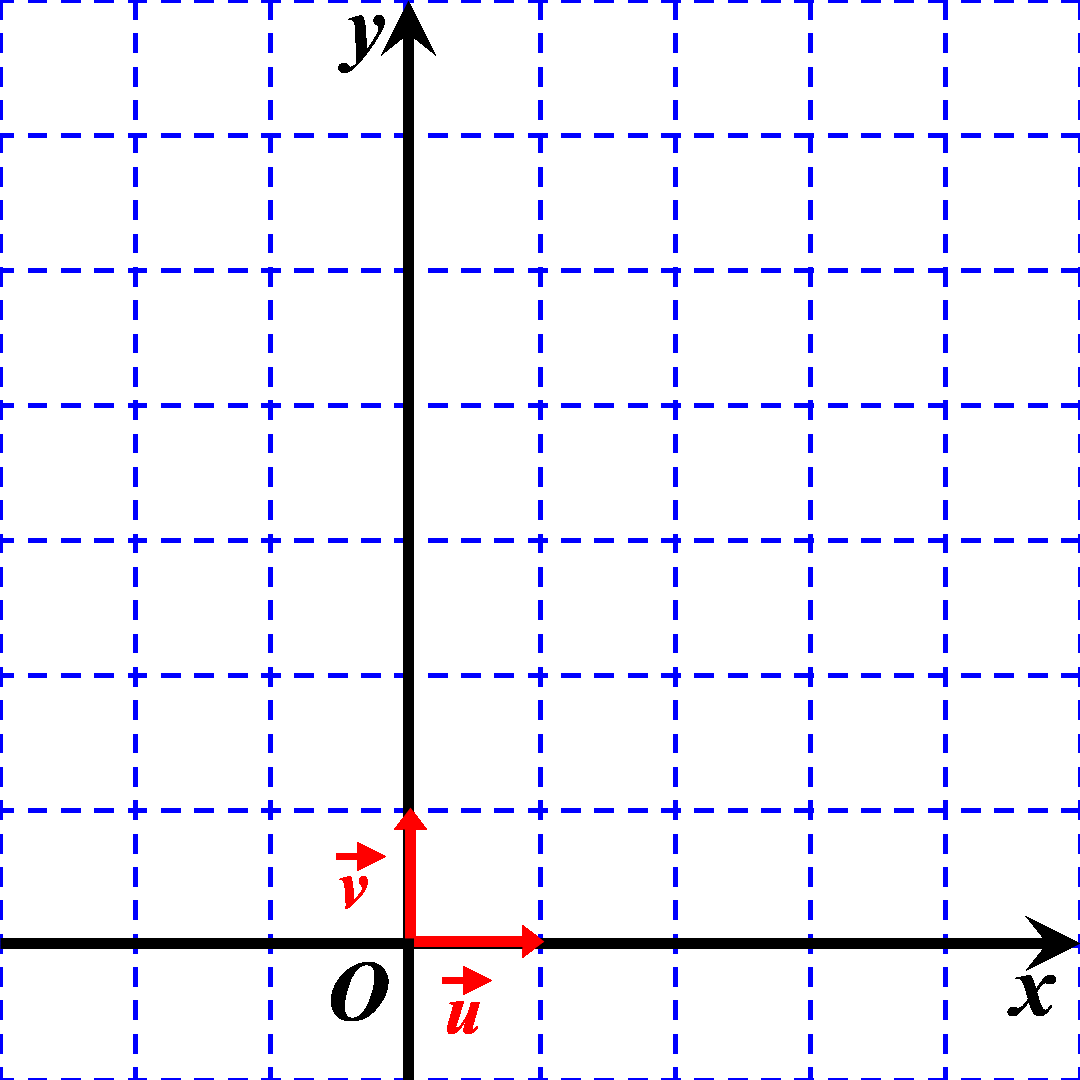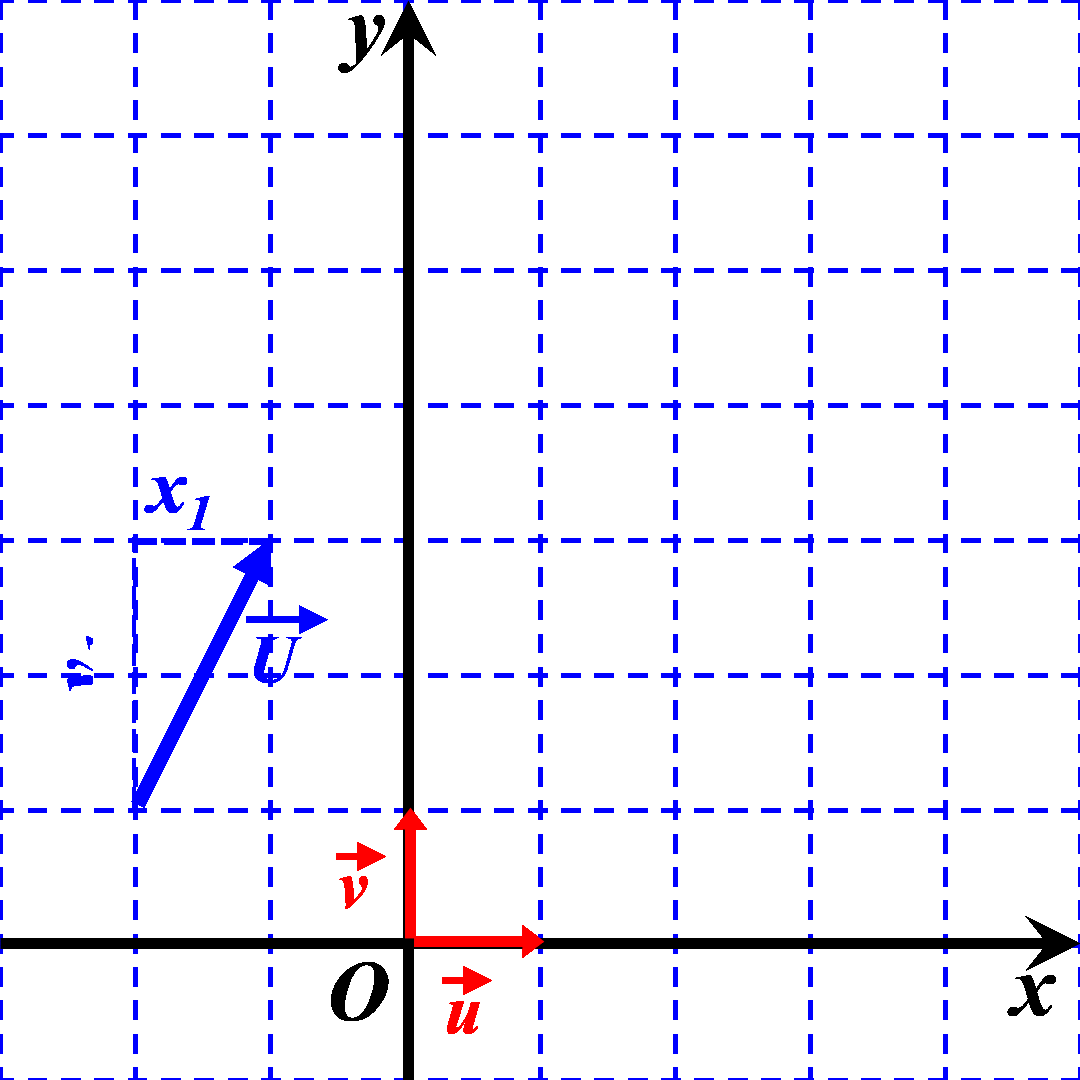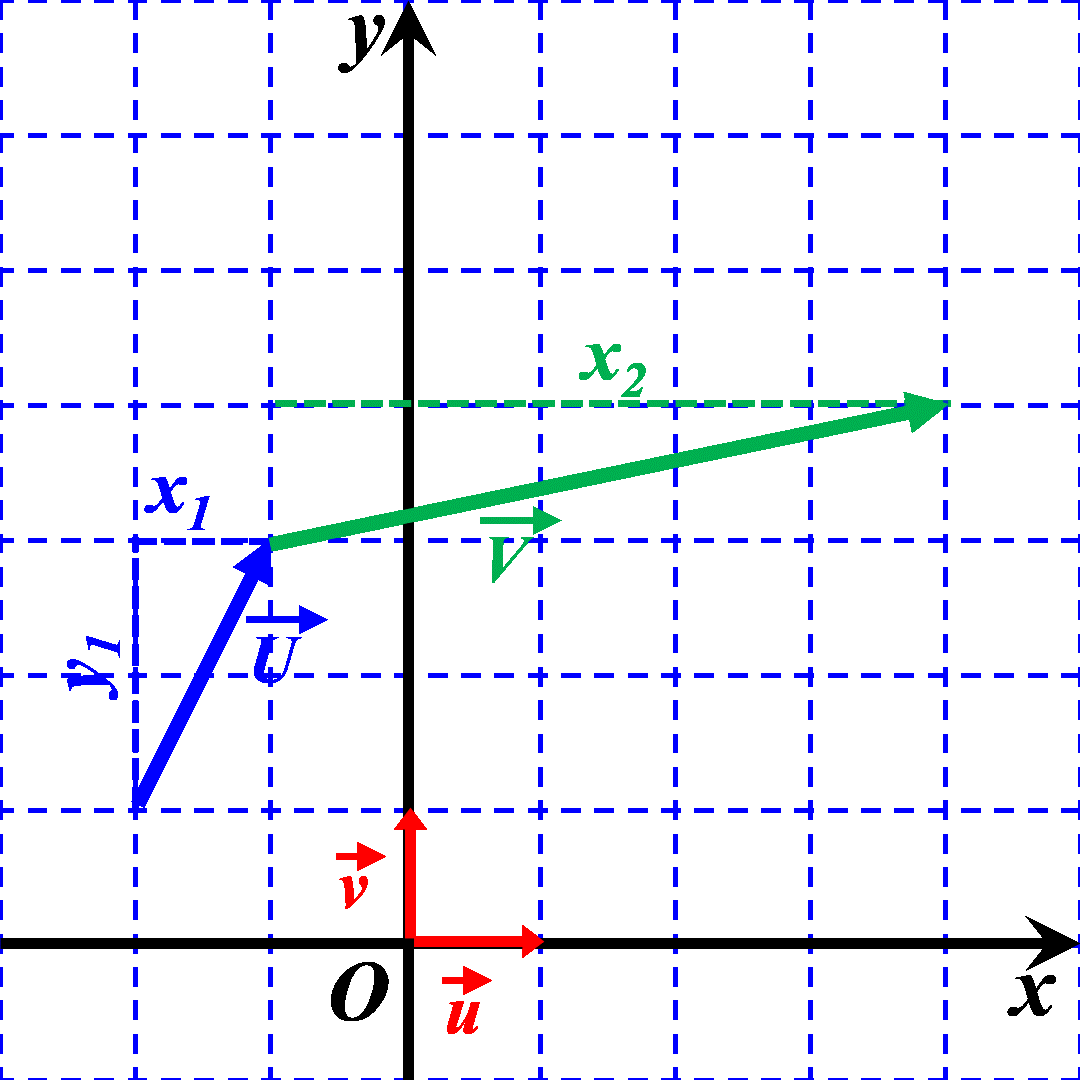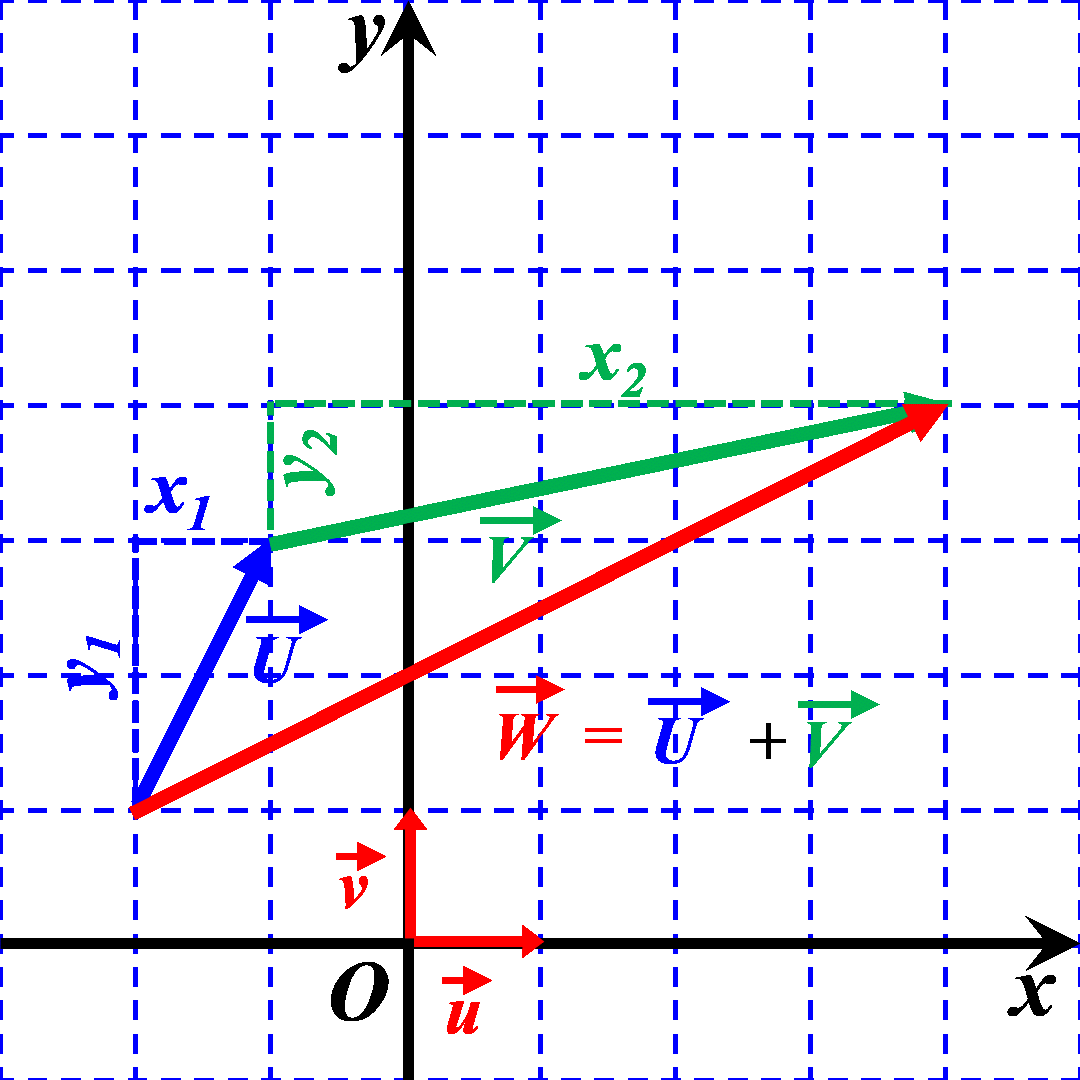
C43. Coordonnées d’un vecteur somme.
|
On considère deux points vecteur $\overrightarrow U$ et $\overrightarrow V$ de coordonnées : $\overrightarrow U \left ((x_1 \ ; \ y_1 \right )$ et $\overrightarrow V \left ((x_2 \ ; \ y_2 \right )$.
|
 |
Exemple :
Dans un repère, on considère les vecteurs : $\overrightarrow U \ = \ \left ( 2 \ ; \ 4 \right ) \ ; \ \overrightarrow V \ = \ \left ( -1 \ ; \ 3 \right ) \ ; \overrightarrow W \ = \ \left ( -2 \ ; \ -4 \right )$
Déterminer les coordonnées des vecteurs :
$\overrightarrow A \ = \overrightarrow U \ + \ \overrightarrow V \ ; \ \overrightarrow B \ = \overrightarrow U \ + \ \overrightarrow W \ ; \ \overrightarrow C \ = \overrightarrow V \ + \ \overrightarrow V \ ; \ \overrightarrow D \ = \overrightarrow U \ - \ \overrightarrow V \ ; \ \overrightarrow E \ = \overrightarrow V \ - \ \overrightarrow W $
.....................................................................................................................
.....................................................................................................................
.....................................................................................................................
.....................................................................................................................
.....................................................................................................................
C43. Coordonnées d’un vecteur somme.
|
On dit que les vecteurs sont COLINEAIRES. ils ont MEME DIRECTION. |
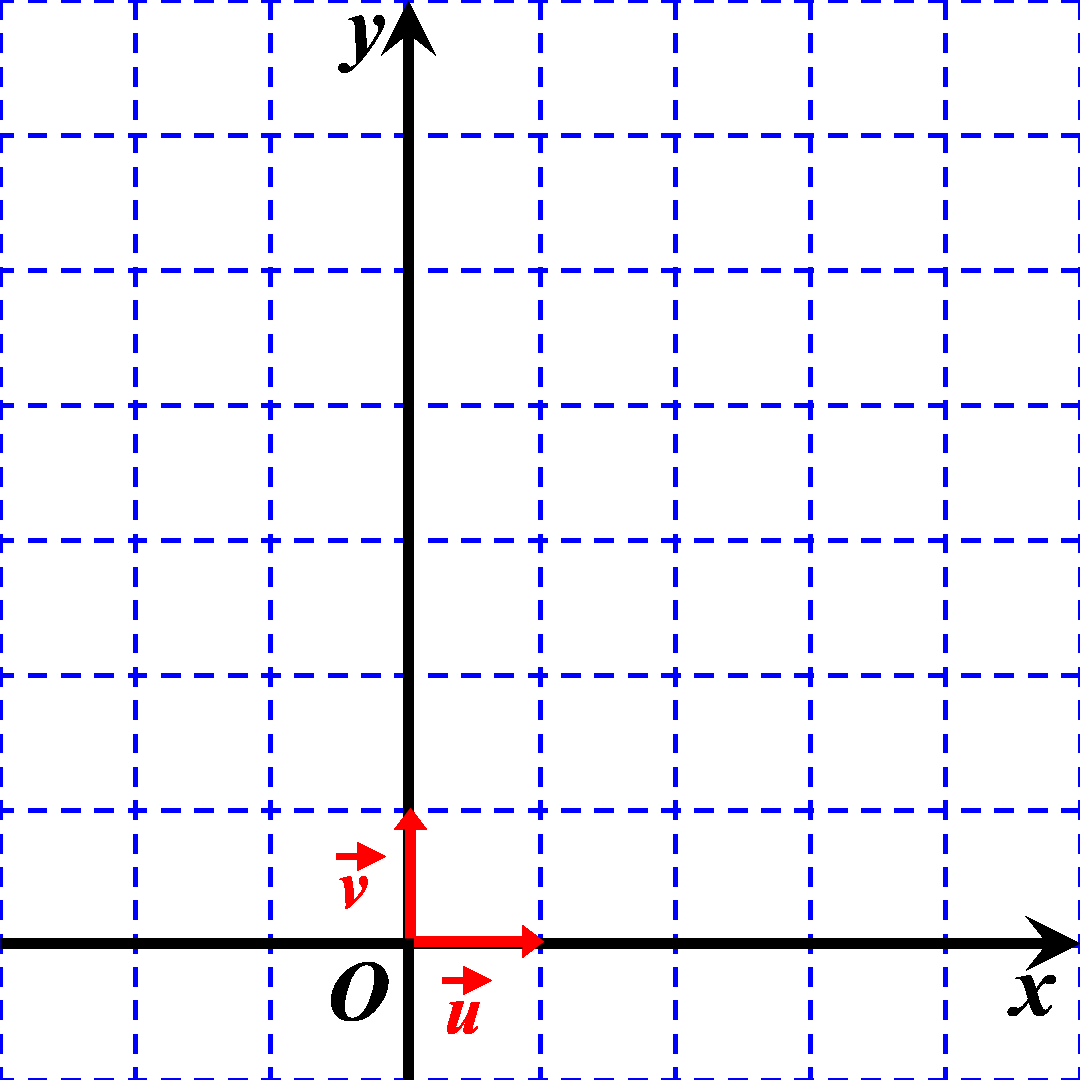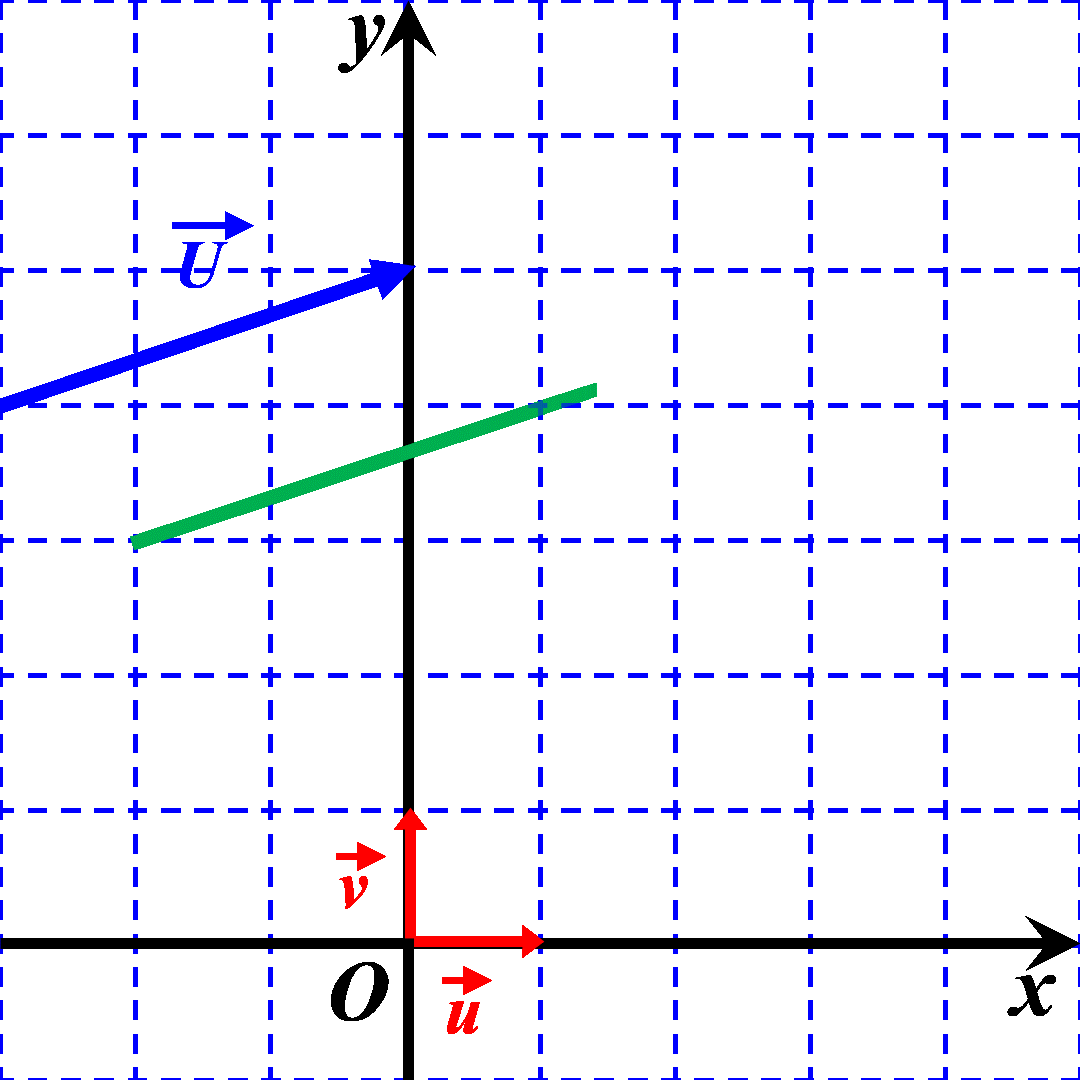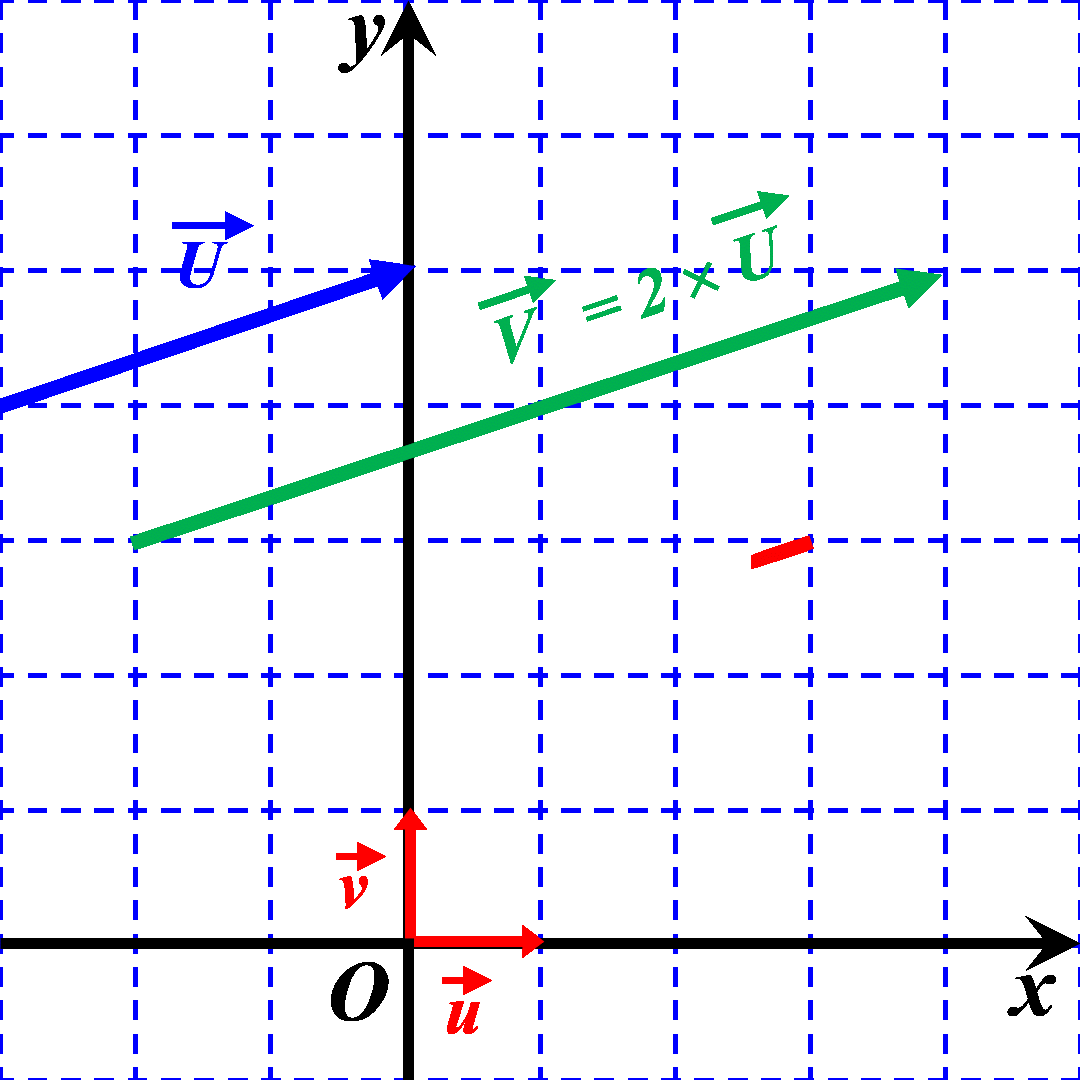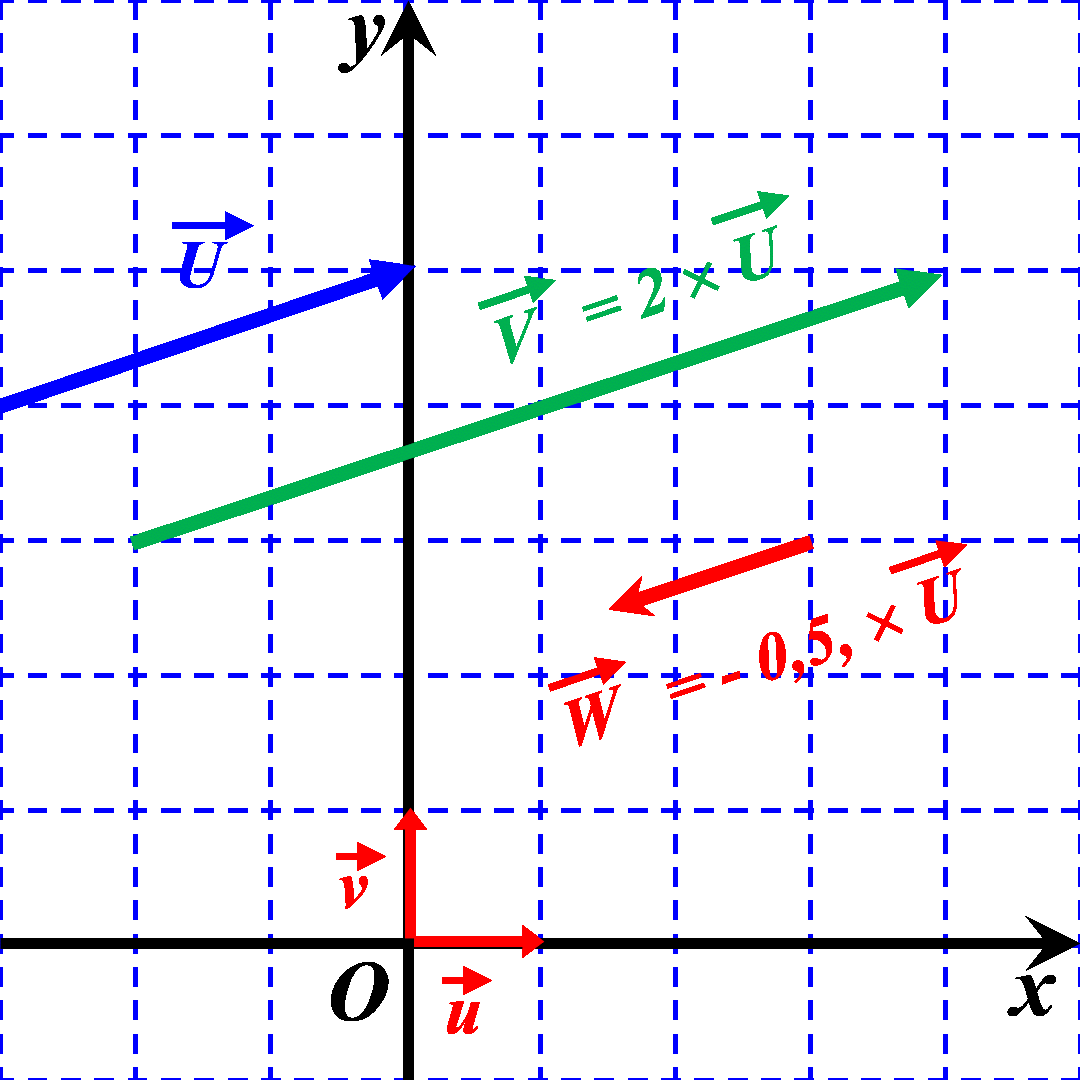 |
C45. Coordonnées du milieu d'un segment.
|
|
 |
Exemples :
On considère les points $A \left ( 1 \ ; \ 4 \right )$, $B \left ( -5 \ ; \ 2 \right )$ et $ C \left ( -3 \ ; \ -3 \right )$
Déterminer les coordonnées de $I$, $J$ et $K$, milieux respectifs des segments $\left [AB \right ]$ ; $\left [ AC \right ]$ et $\left [ BC \right ]$.
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
C46. Norme d'un vecteur.
|
|
 |
Exemples :
On considère les points $A \left ( 1 \ ; \ 4 \right )$, $B \left ( -5 \ ; \ 2 \right )$ et $ C \left ( -3 \ ; \ -3 \right )$
Déterminer les longueurs des segments $\left [AB \right ]$ ; $\left [ AC \right ]$ et $\left [BC \right ]$.
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
Ajouter un commentaire
