Tendance centrale et dispersion
ACTIVITES
A1. Travaux pratiques en chimie.
|
Les élèves d’une classe de Seconde ont mesuré le pH d’une solution lors d’une séance de TP. L’appareil donne une valeur à 0,01 près. |
 |
Les mesures sont répertoriées dans le tableau ci-dessous. :
|
7,01 |
7,04 |
6,92 |
7,11 |
7,38 |
7,05 |
7,25 |
6,82 |
|
7,11 |
7,23 |
7,28 |
7,37 |
7,02 |
7,15 |
7,15 |
7,31 |
|
7,13 |
6,81 |
7,26 |
6,90 |
7,28 |
7,06 |
7,18 |
6,92 |
A11. 1ère étude.
$\bullet$ Quel est le caractère étudié ?
Le caractère étudié est le $pH$ de la solution.
$\bullet$ De quel type de caractère s’agit-il ?
Il s'agit d'une série de valeurs distinctes. C'est un caractère quantitatif discret.
$\bullet$ Dans quel intervalle sont comprises les mesures ?
La valeur la plus petite est $pH_{min} = 6,81$. La valeur la plus grande est $pH_{max} = 7,31$.
$6,81 \ < \ pH \ < \ 7,31$.
$\bullet$ Quelle est la valeur moyenne de cette expérience ?
La valeur moyenne du $pH$ est : $pH_{moy} \ = \ \dfrac{7,01+7,04+6,92+.....+ 7,18+6,92}{24} = \dfrac{170,74}{24} = 7,10$
A12. 2ème étude.
|
On se propose de classer les résultats dans le tableau suivant :
$\bullet$ De quel type de caractère s’agit-il ? Il s'agit d'une série de valeurs classées par intervalle. C'est un caractère quantitatif continu. $\bullet$ Représenter cette série statistique à l’aide d’un graphique adapté dans le repère ci-contre. |
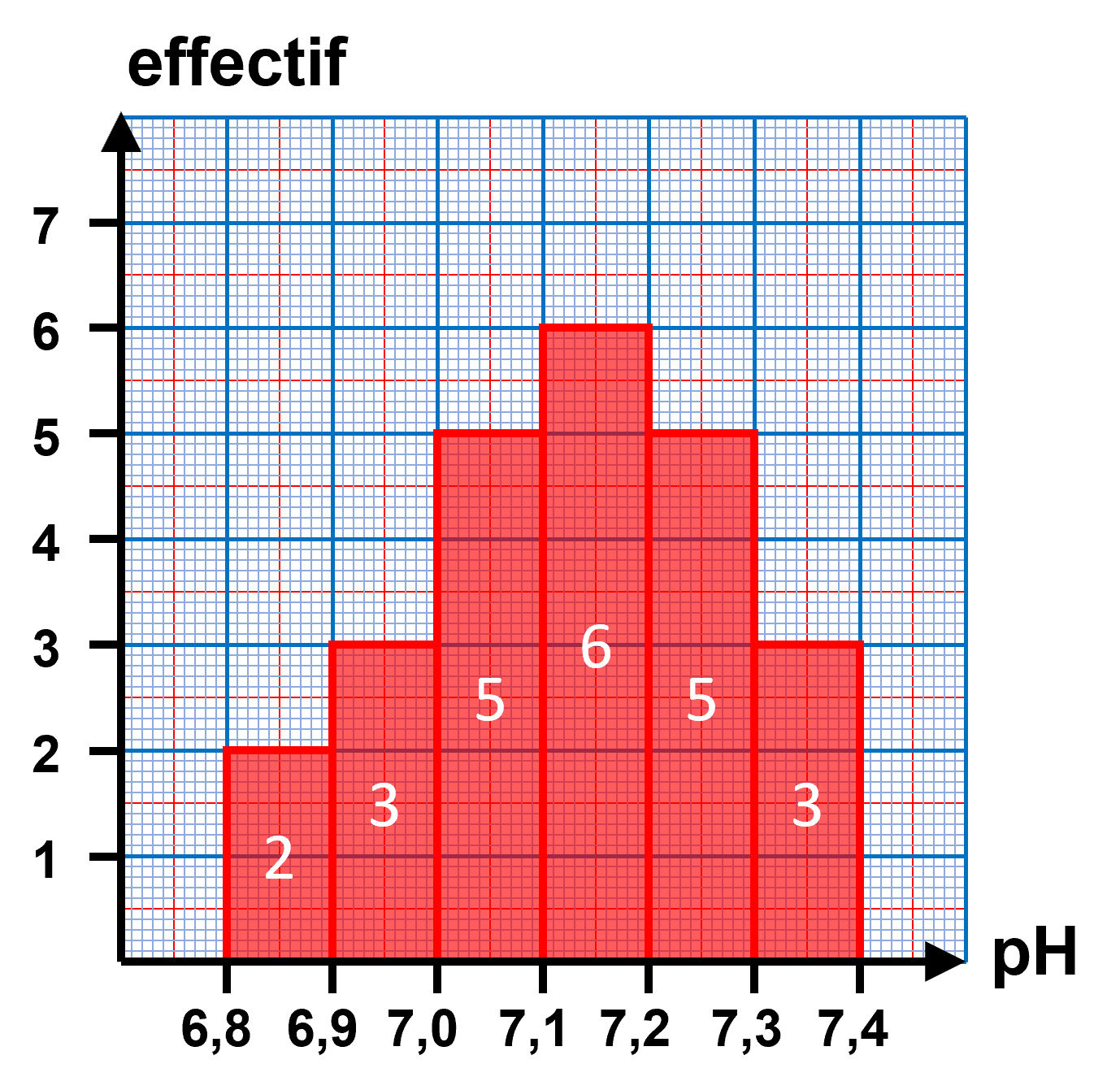 |
|
$\bullet$ Représenter les ECC de cette série statistique. $\bullet$ Quelle est la valeur médiane ? Pour une valeur de l'effectif égal à $\dfrac{24}{2}=12$ : La valeur du $pH$ est comprise dans l'intervalle $[7,10;7,20[$ : La valeur médiane est : $Me = 7,15$ $\bullet$ Quelle est la signification de cette valeur ? C'est la valeur du caractère telle que la moitié de l'efcctif y soit inférieure. $\bullet$ Quelle est la valeur du pH telle qu’un quart de l’effectif total soit inférieur à cette valeur ? Pour une valeur de l'effectif égal à $\dfrac{24}{4}=6$ : La valeur du $pH$ est comprise dans l'intervalle $[7,00;7,10[$ : La valeur du caractère est $7,05$ $\bullet$ Comment s’appelle cette valeur ? On l'appelle le 1er quartile, qu'on note $Q_1$ $\bullet$ Quelle est la valeur du pH telle que trois quarts de l’effectif total soit inférieur à cette valeur ? Pour une valeur de l'effectif égal à $\dfrac{3 \times 24}{4}=18$ : La valeur du $pH$ est comprise dans l'intervalle $[7,20;7,30[$ : La valeur du caractère est $7,25$ $\bullet$ Comment s’appelle cette valeur ? On l'appelle le 3ème quartile, qu'on note $Q_3$ |
 |
$\bullet$ Compléter le tableau suivant.
|
pH |
Centre de classe $x_i$ |
Effectif $n_i$ |
$n_i \ \times \ x_i$ |
|
$[6,80;6,90[$ |
$6,85$ |
$2$ |
$^\color{blue}{6,85 \times 2} \ 13,70$ |
|
$[6,90;7,00[$ |
$6,95$ |
$3$ |
$^\color{blue}{6,95 \times 3} \ 20,85$ |
|
$[7,00;7,10[$ |
$7,05$ |
$5$ |
$^\color{blue}{7,05 \times 5} \ 35,25$ |
|
$[7,10;7,20[$ |
$7,15$ |
$6$ |
$^\color{blue}{7,15 \times 6} \ 42,90$ |
|
$[7,20;7,30[$ |
$7,25$ |
$5$ |
$^\color{blue}{7,25 \times 5} \ 36,25$ |
|
$[7,30;7,40[$ |
$7,35$ |
$3$ |
$^\color{blue}{7,35 \times 3} \ 22,05$ |
|
TOTAUX |
$24$ |
$171,00$ |
$\bullet$ Calculer la moyenne de cette série statistique.
$pH_{moy} = \dfrac{6,85 \times 2 + 6,95 \times 3 + ... + 7,35 \times 3}{24}$
$pH_{moy} = \dfrac{171,00}{24} = 7,13$
$\bullet$ Représenter les quatre valeurs précédemment définies sur l’axe ci-dessous.
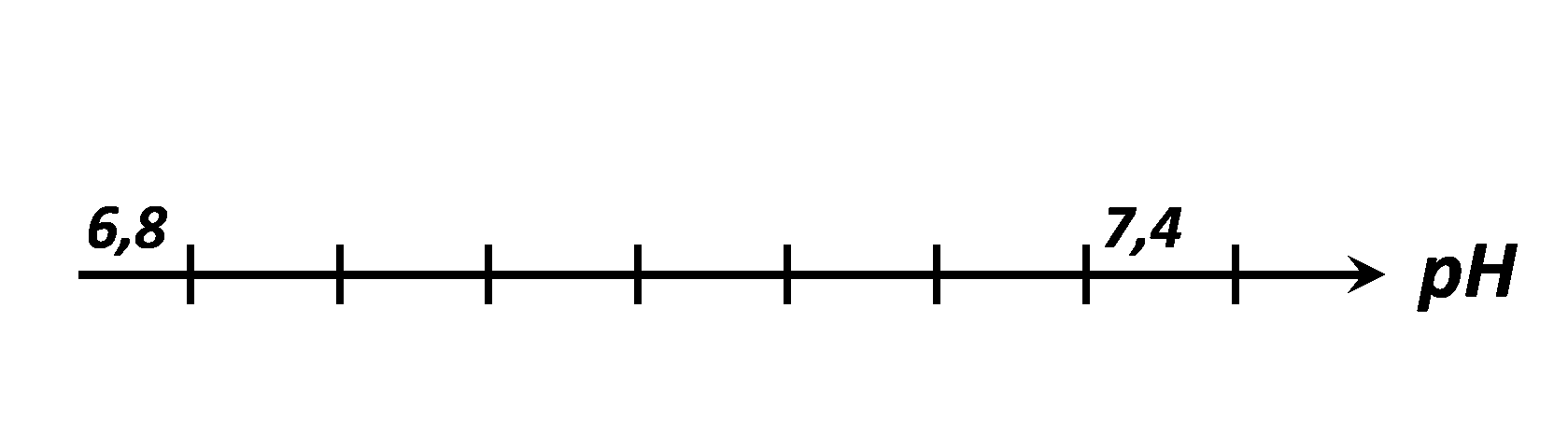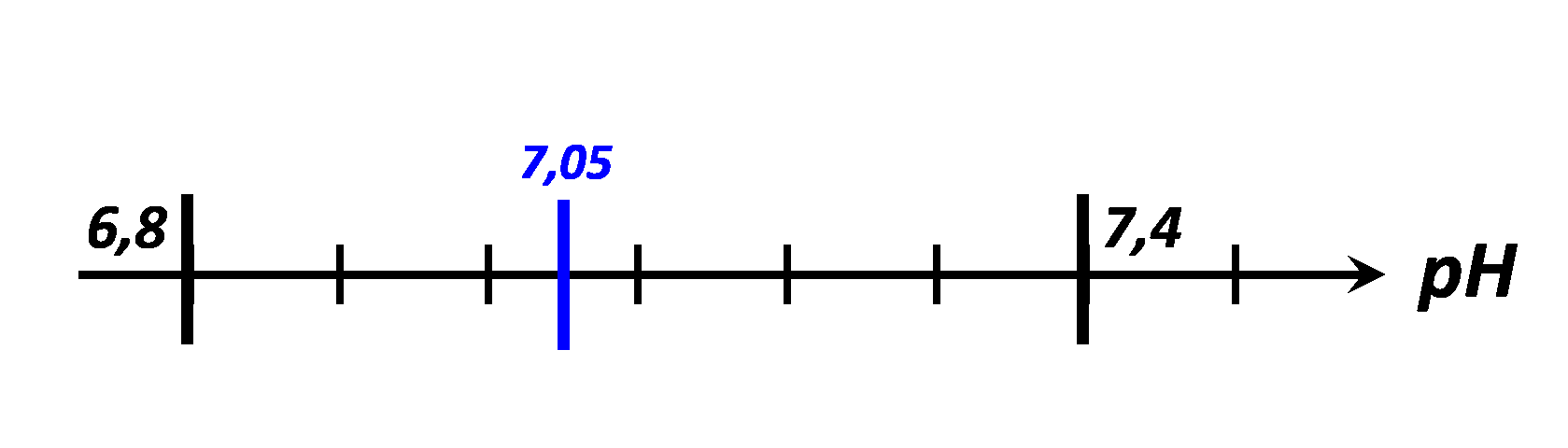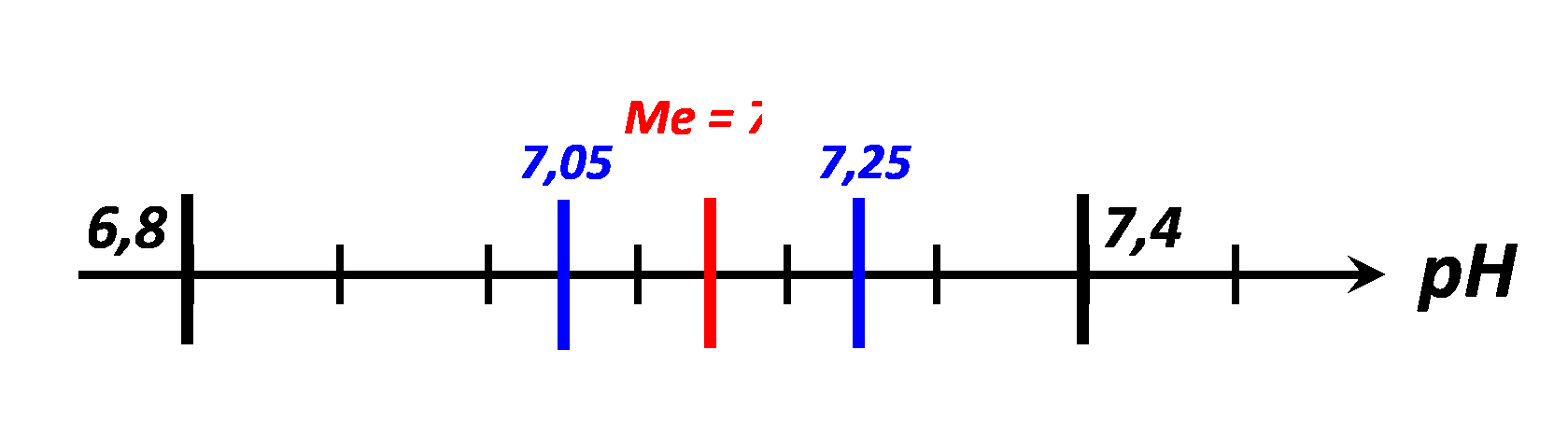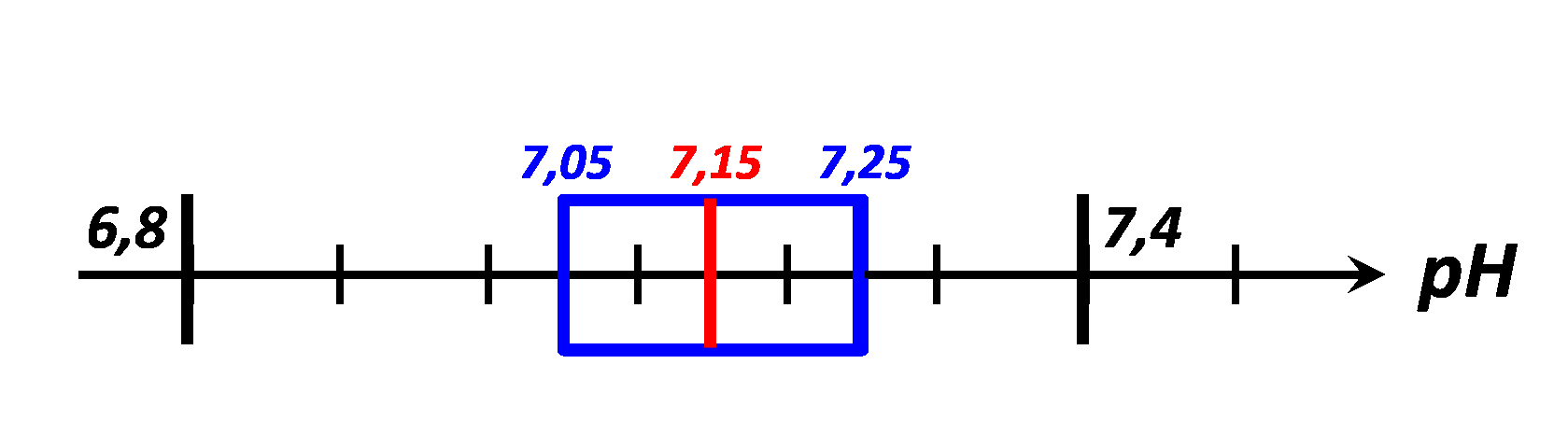
A13. Retrouver toutes ces valeurs à l’aide de la calculatrice.
|
$\bullet \ Me \ = \ ...........$ $\bullet \ Q_1 \ = \ ...........$ $\bullet \ Q_3 \ = \ ...........$ $\bullet \ Moyenne \ = \ ...........$ |
 |
A2. Tour de France.
|
Voici les distances en km de chacune des étapes des Tours de France 2018 et 2019. Les distances ont été rangées par ordre croissant.
|
 |
||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||
Etudes.
|
Pour l'année 2018 : |
Pour l'année 2019 : |
|
$\bullet$ Déterminer l'étendue. Il s'agit de l'écart entre la plus grande valeur et la plus petite valeur. $231-108 = 123 \ km$ $\bullet$ Déterminer la longueur moyenne d’une étape. $\dfrac{108+154+...+218+231}{17}= 180 \ km$ $\bullet$ Déterminer la longueur médiane d’une étape. $Me = 181 \ km$ $\bullet$ Déterminer les 1er et 3ème quartiles. $Q_1=\dfrac{169+172}{2}=170,5 \ km$ $Q_3=\dfrac{189+192}{2}=190,5 \ km$ |
$\bullet$ Déterminer l'étendue. $231-117 = 114 \ km$ $\bullet$ Déterminer la longueur moyenne d’une étape. $\dfrac{117+123+...+230+231}{19}= 183 \ km$ $\bullet$ Déterminer la longueur médiane d’une étape. $Me = 192 \ km$ $\bullet$ Déterminer les 1er et 3ème quartiles. $Q_1=167 \ km$ $Q_3=214 \ km$ |
Aide à la détermination de la médiane est des quartiles : http://coyote-physique.e-monsite.com/pages/correction-bp/mediane-et-quartiles.html
Comparaisons.
$\bullet$ Représenter sur chaque axe, la longueur moyenne, la longueur médiane, les 1er et 3ème quartiles.
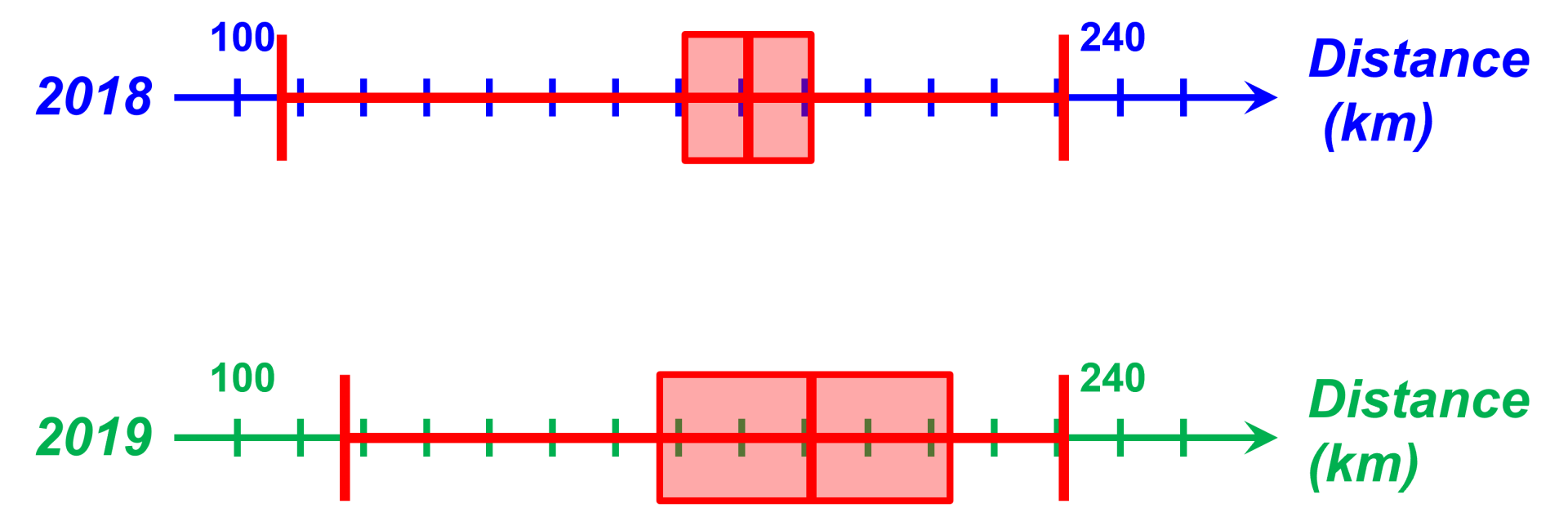
$\bullet$ En comparant pour chaque Tour, l’écart entre les 1er et 3ème quartiles, indiquer en quelle année les étapes présentent la plus grande dispersion.
..................................................................................................................................................................................................................................................
..................................................................................................................................................................................................................................................
A3. Boite mail.
|
Le diagramme en bâtons ci-contre représente le nombre de mails envoyés par les élèves d’une classe de seconde au cours d’une journée. A31. Exploitation du graphique. $\bullet$ Quel est le nombre d'élèves dans la classe ? $4+2+4+9+7+3+2+1 \ = \ 32$ $\bullet$ Quel est le nombre total de mails envoyés par les élèves ? $2 \times 4+3 \times 2+...+ 8 \times 1 = 163$ $\bullet$ En déduire le nombre moyen de mails envoyés par un élève de la classe. $\dfrac{163}{32}=5,1$ Le nombre moyen de mails envoyés est donc de 6 mails par élève. |
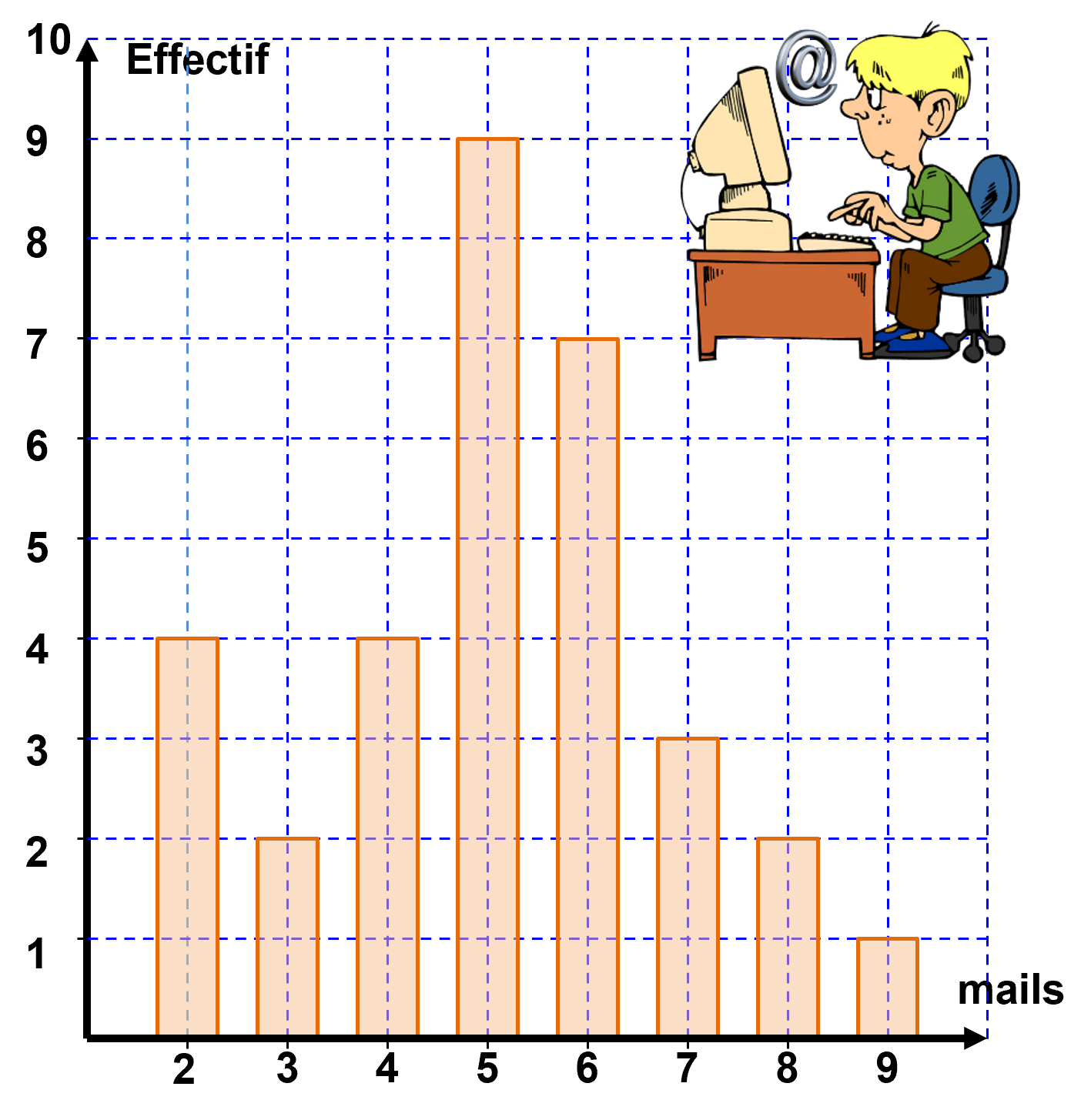 |
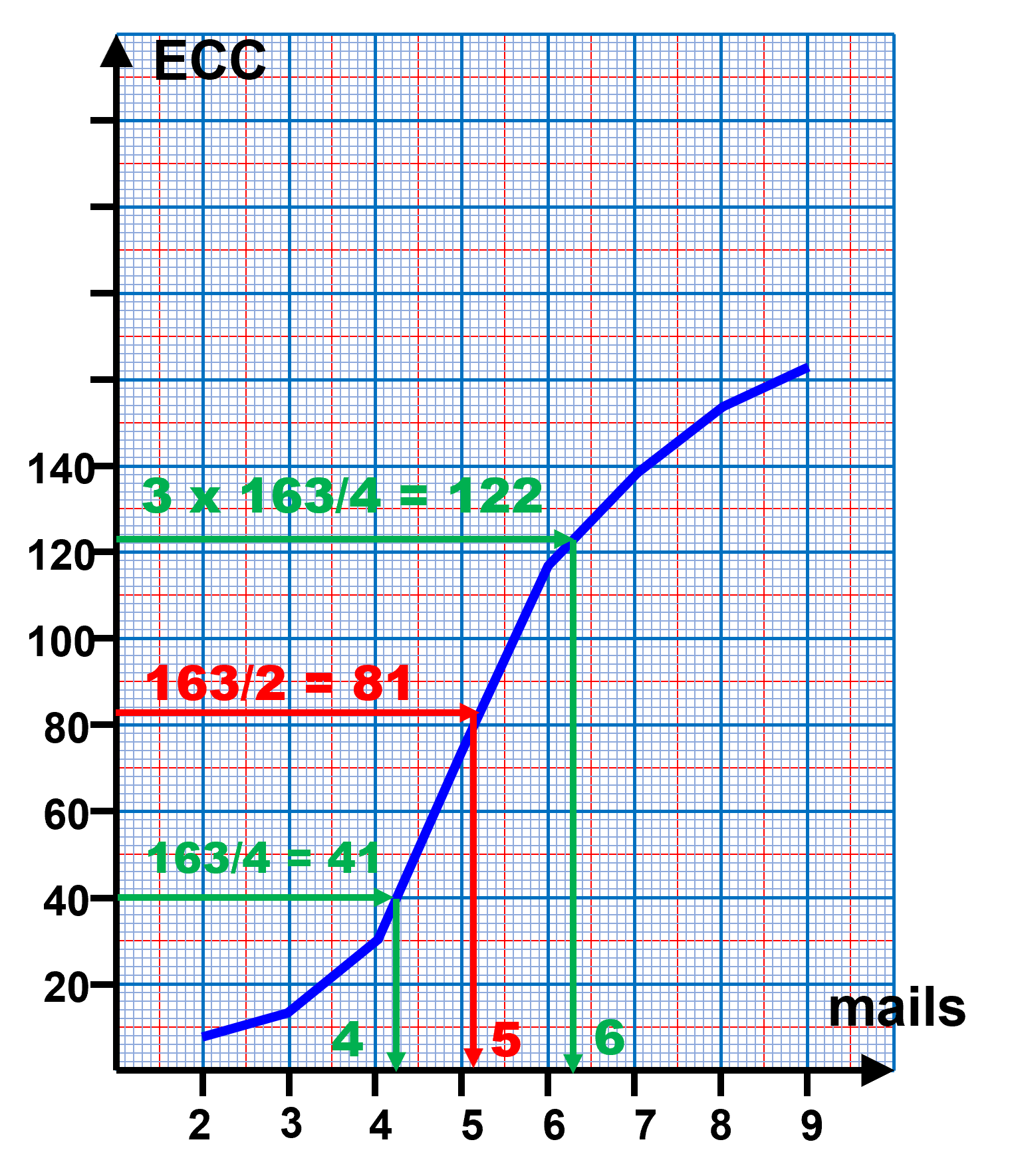
$\bullet$ A l’aide du graphe ci-contre, déterminer la valeur médiane de cette série.
$Me= 5 \ mails$ $\bullet$ A l’aide du graphe ci-contre, déterminer les 1er et 3ème quartiles de cette série
$Q_1= 4 \ mails$ ; $\ Q_3= 6 \ mails$ |
 |
A32. Retrouver toutes ces valeurs à l’aide de la calculatrice.
|
$\bullet \ Me \ = \ ...........$ $\bullet \ Q_1 \ = \ ...........$ $\bullet \ Q_3 \ = \ ...........$ $\bullet \ Moyenne \ = \ ...........$ |
 |
Ajouter un commentaire
