Fluide au Repos
ACTIVITES
A1. Plongée en apnée.
Comment expliquer l'apparition de cette gêne ?
|
|
|
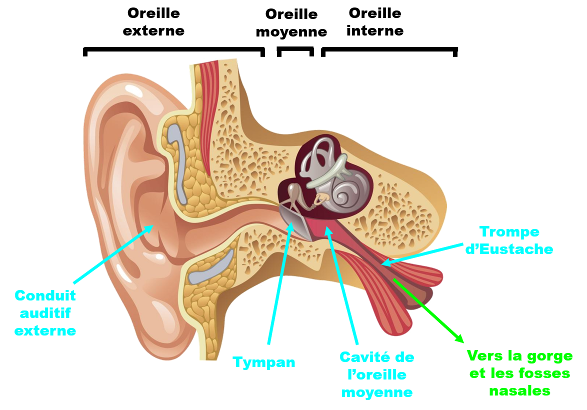
Doc 2 : Schéma de l'oreille. La trompe d'Eustache est le conduit qui relie l'oreille au nez à la gorge. Elle contient de l'air. À 10 mètres de profondeur, le tympan d'une oreille peut être modélisé par une surface plane Σ d'aire S = 60 mm2, soumise à : • La force pressante $\overrightarrow {F_1}$ exercée par l'air à l'intérieur du tympan, à la pression interne P1 = 1 bar = 1,0.105 Pa • La force pressante $\overrightarrow {F_2}$ exercée par l'eau à l'extérieur du tympan, à la pression extérieure P2 = 2 bar = 2,0.105 Pa. |
Dans les deux cas :
• Calculer la norme F1 de la force pressante exercée par l’air à l’intérieur du tympan d’une oreille et la norme F2 de la force pressante exercée par l’eau à l’extérieur du tympan à 10 mètres de profondeur.
• Réaliser un schéma en coupe du modèle du tympan d’une oreille en représentant les forces $\overrightarrow {F_1} \ et \ \overrightarrow{F_2}$ avec l’échelle
1 cm ↔ 3 N.
• Expliquer pourquoi les plongeurs ne sentent pas de gêne à la surface et pourquoi une gêne apparaît en profondeur.
• La manœuvre dite "équilibrage de pression" consiste à se pincer le nez et à souffler modérément en conservant la bouche fermée afin d’augmenter la pression de l’air qui se trouve dans l’oreille moyenne. Expliquer comment cette manœuvre permet de supprimer la gêne ressentie au niveau des oreilles lors de la plongée.
A2. Loi fondamentale de la statique des fluides.
|
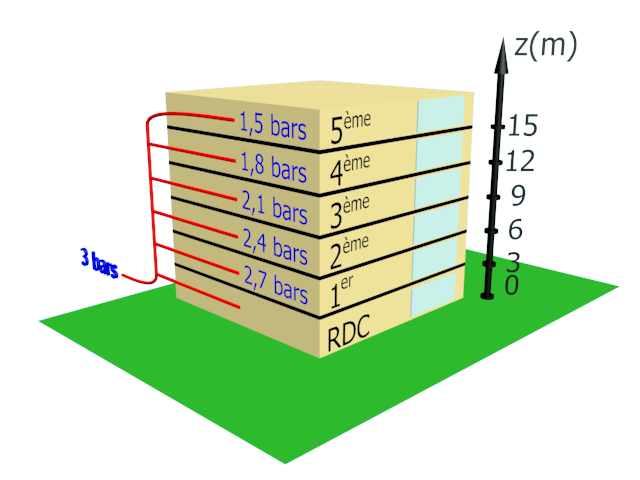
En plongée, la pression exercée par l'eau s'accroît au fur et à mesure que la hauteur d'eau situé au-dessus plongeur augmente. |
 |
Élaborer et mettre en œuvre un protocole expérimental permettant de vérifier, dans le cas de l'eau, la relation mathématique entre la variation de pression entre deux points d'un fluide et leur différence d'altitude.
|
|
|
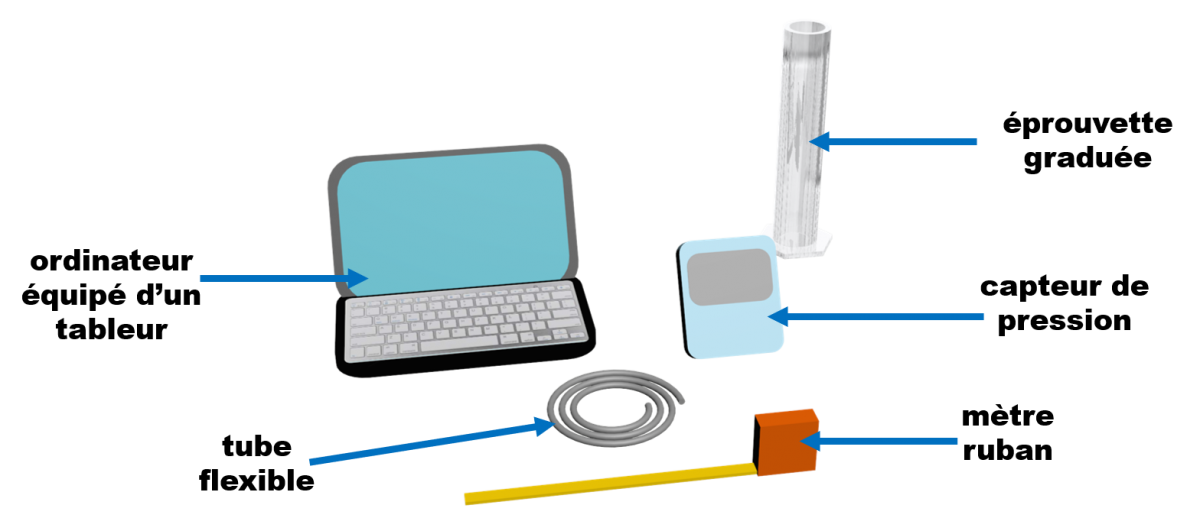
• Décrire le protocole expérimental avec du texte et des schémas.
• Réaliser le montage expérimental et les mesures nécessaires.
• Traiter les résultats à l’aide d’un tableur-grapheur en tenant compte de la dispersion des mesures.
• Vérifier que la loi de la statique des fluides est validée.
A3. Pression et volume d'un gaz.
|
En montagne, un randonneur effectuant une ascension observe que le volume de son paquet de chips augmente et que la pression atmosphérique affichée sur son altimètre diminue. |
 |
Comment varie le volume d'un gaz lorsque sa pression varie à température constante ?
|
Document 1 : Loi de Mariotte. A température constante et pour une quantité de gaz donné, le produit de la pression P par le volume V d'un gaz est constant. |
|
Document 2 : Protocole.
|
$\bullet$ Appliquer le protocole en remplissant la seringue à un volume initial $V_0 = 20 \ mL$.
$\bullet$ Appliquer le protocole en remplissant la seringue à un volume initial $V_0 = 30 \ mL$.
$\bullet$ Appliquer le protocole en remplissant la seringue à un volume initial $V_0 = 40 \ mL$.
$\bullet$ A l’aide des résultats précédents, confirmer ou infirmer la loi de Mariotte.
$\bullet$ Dans le cas où la loi de Mariotte serait vérifiée, indiquer de quel paramètre dépend la valeur de la constante k et présenter sa valeur dans chaque cas.
$\bullet$ En gardant le piston de la seringue immobiles, poser la paume de la main sur le cylindre pour chauffer l’air qu’il contient. Observer comment évolue la pression.
$\bullet$ De quels paramètres dépend la valeur de la constante k ?
$\bullet$ A l’aide des résultats précédents, expliquer le gonflement d’un paquet de chips fermé au cours d’une ascension en montagne.
EXERCICES : 8 ; 10 ; 12 ; 13 ; 14 ; 15 ; 16 ; 17 ; 19 ; 21 ; 23 ; 24 ; 26 ; 29 ; 32 ; 34 ; 39 ; 40.
P 209 à 218
COURS
C1. Grandeurs macroscopiques de description d'un fluide.
C11.Les trois états de la matière.
On nomme entité les molécules atomes et ions qui forment la matière. Les 3 états peuvent être décrits ainsi :
|
 |
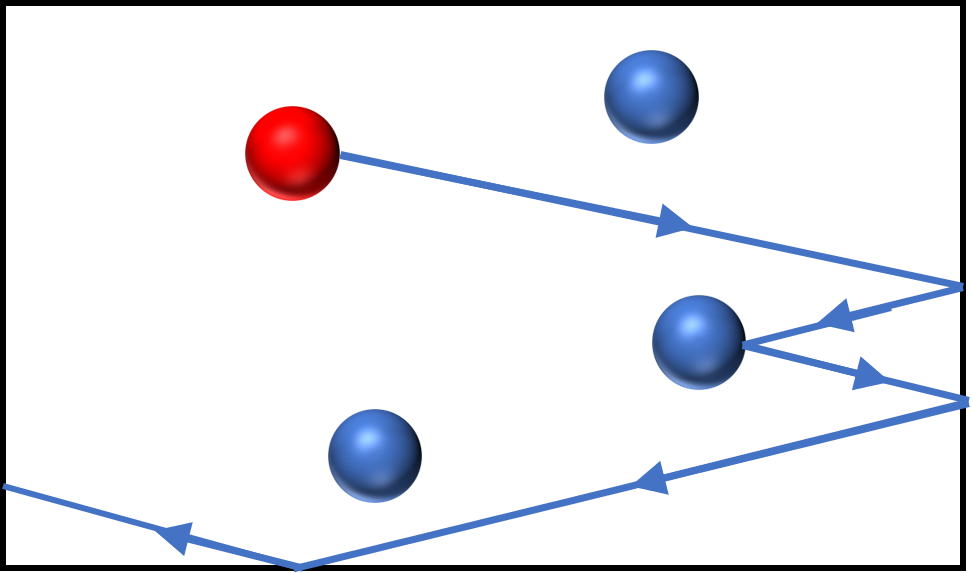
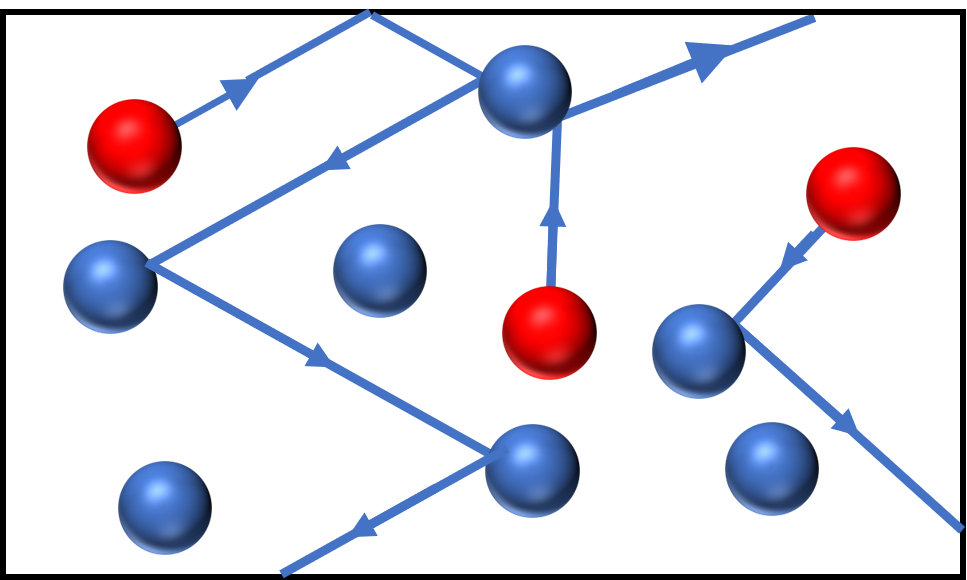
Un fluide est caractérisé par un mouvement incessant et désordonné de ses entités : c'est le cas de l'état liquide et de l'état gazeux.
|
état gazeux |
état liquide |
C12.Masse volumique.
Dans un volume V donné, le nombre d'entités, donc la masse de matière m, est plus grande dans l'état liquide compact que dans l'état gazeux dispersé.
La masse volumique et le rapport de la masse m de matière au volume V occupé par cette matière :
|
ρ en kg.m-3 m en kg V en m3. |
C13. Temprature.
La température absolue T (exprimée en Kelvin) est une grandeur macroscopique qui caractérise l'agitation des entités dans un milieu.
La température exprimée en kelvin et la température θ exprimée en degrés Celsius sont liées.
T = θ + 273,15
C14. Pression.
|
Lorsqu'une entité rebondit sur la paroi d'un récipient, son vecteur vitesse est modifié. La paroi exerce donc une force sur cette entité, donc les entités exerce une force opposée sur la paroi. La pression P est une grandeur macroscopique qui mesurent l'action mécanique qu'un fluide exerce sur une surface donnée. La pression s'exprime en Pascal (Pa). |
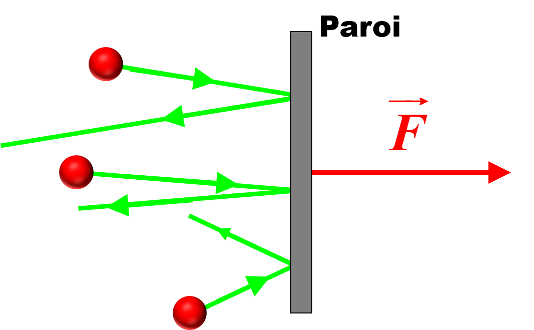 |
C2. Action d'un fluide sur une surface.
|
Un fluide occupe la totalité de l'espace mis à sa disposition, à l'exception de la surface supérieure d'un liquide. Il n'est arrêté que par les parois du récipient qui le contient.
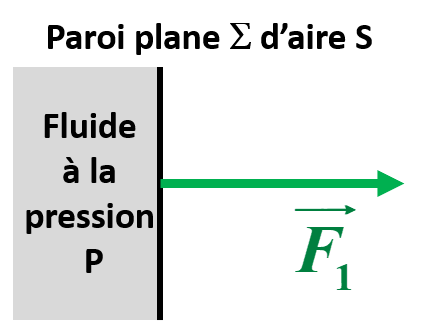
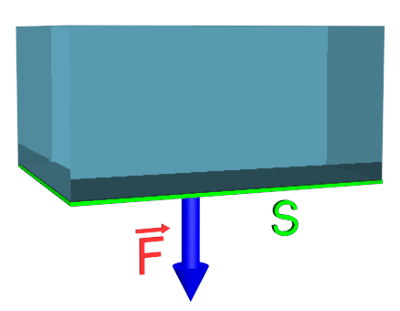
La force pressante $\overrightarrow F$ exercée par un fluide sur une surface plane S est $\overrightarrow F = -P \times S \times \overrightarrow n $, où P est la pression du fluide au contact de la surface et $\overrightarrow n$ est le vecteur unitaire normal perpendiculaire à la surface dirigé vers le fluide. La pression dans le fluide a donc pour expression :
F en newtons (N) S en mètres carrés (m²) P en Pascals (Pa)
NB : La pression se mesure à l'aide d'un manomètre. |
 |
C3. Modèle de comportement d'un gaz : loi de Mariotte.
|
On diminue le volume d'un récipient en déplaçant le piston et en maintenant constante la température du gaz qu'il contient. Les parois de gauche et de droite se rapprochent, les chocs et rebonds des entités sur ses parois sont plus fréquents, la force pressante donc la pression augmente.
Loi de Mariotte : À température constante et pour une quantité de matière de gaz donnée, le produit de la pression P du gaz par le volume V qu'il occupe est constant : $ P \times V = constante $
|
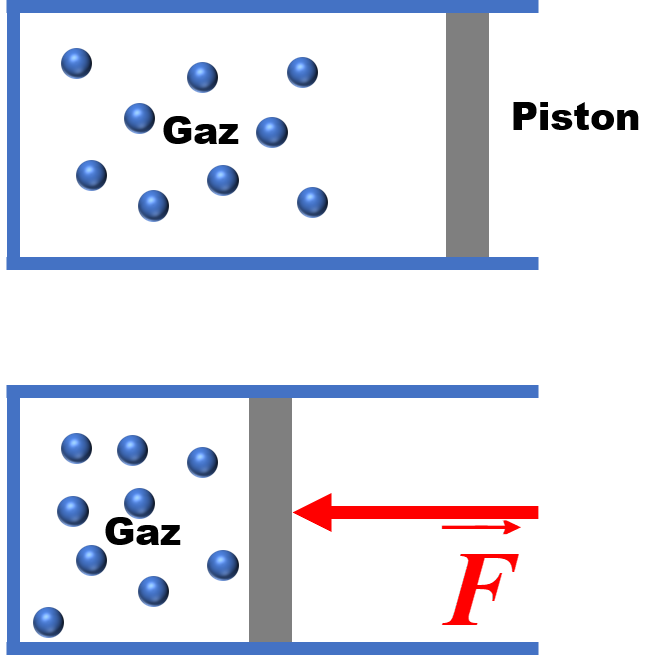 |
NB : La constante n'est ni une constante universelle, ni donnée dans l'énoncé. Il faut toujours traduire la loi de mariotte en considérant le système gazeux dans un état initial, la pression vaut P1 et le volume V1 dans l'état initial, et dans l'état final où la pression vaut P2 et le volume V2 :
$P_1 \times V_1 = P_2 \times V_2 $
C4. Loi fondamentale de la statique des fluides.
C41. Fluide au repos.
|
À l'échelle microscopique, les entités d'un fluide sont en perpétuelle agitation. Un fluide au repos est dépourvu de mouvement global (déplacement de l'ensemble du fluide) ou de mouvement interne observable (déplacement de partie du fluide, tourbillons, vagues).
|
 |
C42. Fluide incompressible.
Un fluide incompressible possède une masse volumique $\rho$
Les gaz sont compressibles.
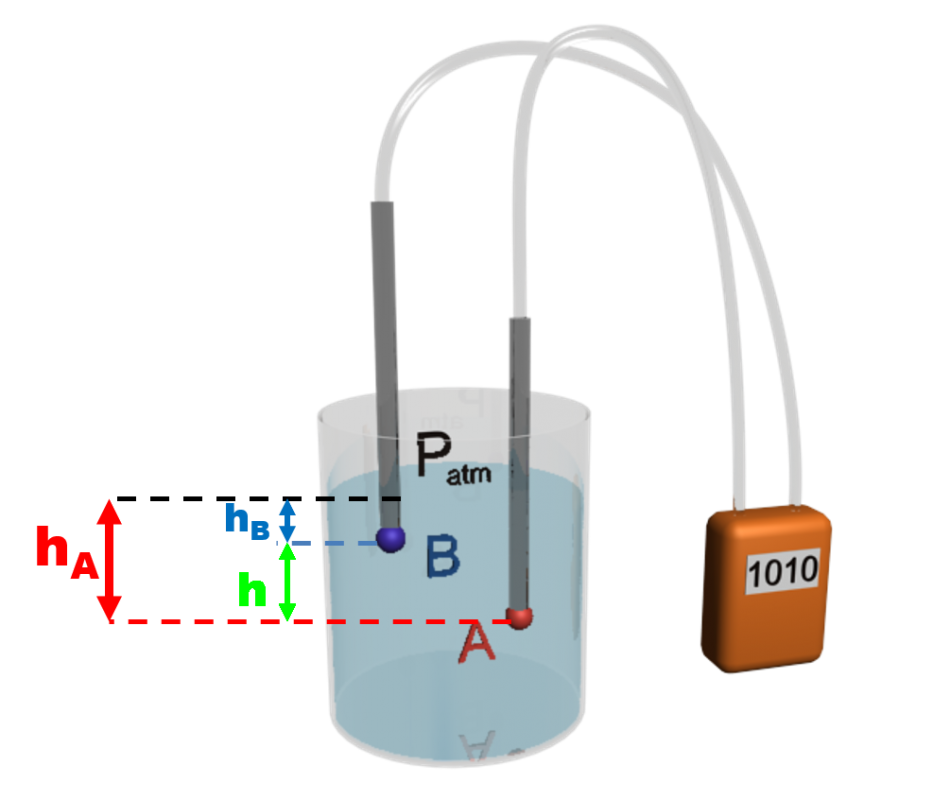
C43. Loi fondamentale de la statique des fluides incompressibles.
La différence ΔP de pression entre deux points est proportionnelle à la différence de Δz de leurs altitudes et elle est proportionnelle à la masse volumique ρ du liquide.
|
 |
Ajouter un commentaire