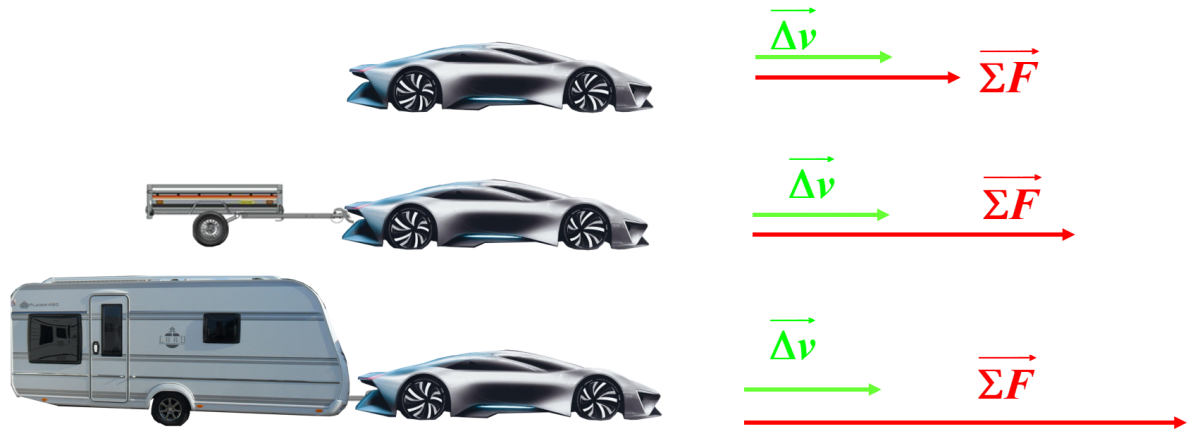
Mouvement d'un système
ACTIVITES
A1. Chute libre.
On a laissé tomber une balle de tennis et une masse de 1 kg du haut de la salle de chimie au troisième étage. Elles sont arrivées en même temps…
Objectif : Quelles sont les caractéristiques du vecteur variation de vitesse dans le cas de la chute libre ?
|
|
Doc 5 : Description du tracé du vecteur vitesse
Doc 6 : Description du tracé du vecteur accélération
Dans les deux cas :
• Décrire la trajectoire des solides.
• Donner l'expression de la vitesse en fonction du temps des solides.
• Donner l'expression de l'accélération en fonction du temps des solides.
• Préciser les unités de ces deux grandeurs (vitesse et accélération).
• Comparer la valeur de l'accélération à une grandeur déjà connue (doc3).
• Quelle est la force subie par ces deux masses tout au long de leur chute ?
• En déduire une relation entre l'accélération et cette force.
A2. Variation du vecteur vitesse lors d'une chute libre.
Avec un trampoline, un gymnaste peut effectuer un saut vertical atteignant jusqu'à 8 m de haut. Il reste alors environ 2 s en l'air pour effectuer sa figure.
Quelles sont les caractéristiques du vecteur variation de vitesse dans le cas de la chute libre ?
|
|
• Sans souci d'échelle, représenter sur un schéma la force qui s'exerce sur le gymnaste en vol dans les 2 phases du mouvement en indiquant le référentiel d'étude choisi. Les forces de frottement de l'air sont négligées.
• À l'aide du doc 3, décrire comment évolue la vitesse du gymnase dans les phases ascendantes et descendantes.
• Pour les 2 phases, représenter en rouge le vecteur vitesse $\overrightarrow {v_1} , \overrightarrow {v_2} ,\overrightarrow {v_8} \ et \ \overrightarrow {v_9} $ avec une échelle judicieusement choisie.
• Pour les 2 phases, calculer et tracer les vecteurs $\overrightarrow {\Delta v_1} \ et \ \overrightarrow {\Delta v_2} $ sachant que $\overrightarrow {\Delta v_i} = \overrightarrow {v_{i+1}} - \overrightarrow {v_{i}} $.
• Décrire la direction, le sens et la variation d'intensité du vecteur $\overrightarrow {\Delta v}$ dans les 2 phases du mouvement.
• Indiquer la force responsable de la variation du vecteur vitesse.
A3.Variation du vecteur vitesse et somme des forces.
Le patinage artistique en couple est un sport qui se pratique sur de la glace. Lors des compétitions, chaque couple exécute plusieurs figurent (portées, pirouettes spirales) afin de marquer un maximum de points.
Quel lien existe entre la force $\overrightarrow F$ exercée par le patineur sur sa partenaire et le vecteur variation de vitesse de celle-ci ? .
|
|
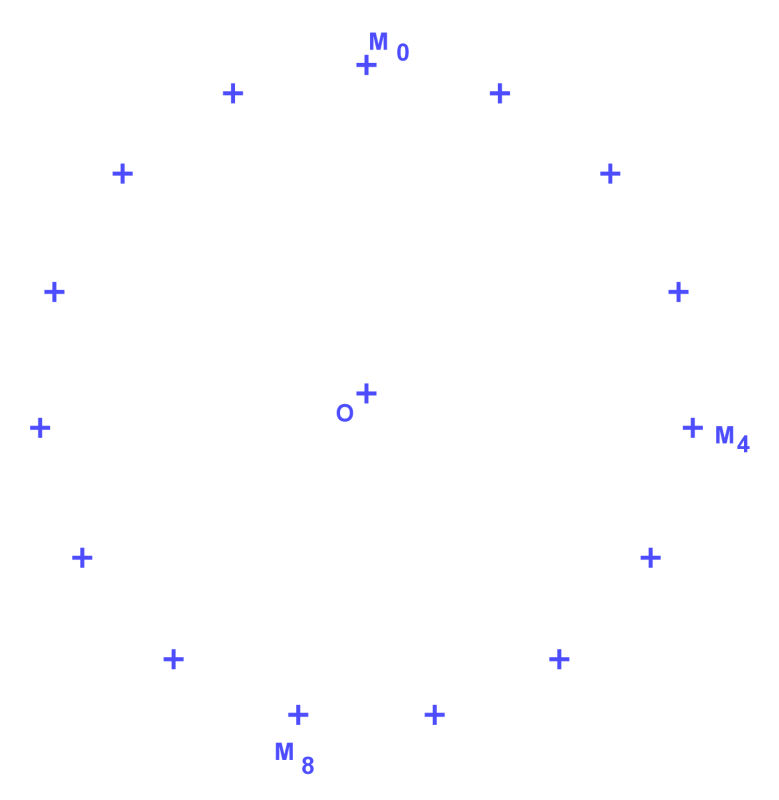
• Préciser à l'aide du docoment la caractéristique du vecteur vitesse du système {patineuse} qui changent le cours du mouvement.
• Sur le document ci-dessous : représenter les vecteurs vitesse instantanée $\overrightarrow {v_1} , \overrightarrow {v_2} ,\overrightarrow {v_9} \ et \ \overrightarrow {v_{10}} $ respectivement aux points M1, M2, M9 et M10.
• Représenter le vecteur variation de vitesse $\overrightarrow {\Delta v_2} $ au point M2. Tracer de même $\overrightarrow {\Delta v_{10}} $ au point M10. Vérifier que chaque vecteur $\overrightarrow {\Delta v} $ a pour direction le rayon du centre et est orientée vers le centre du cercle quelle que soit la date t.
• Montrer que la somme des forces appliquées à la {patineuse} est égale à la force exercée sur elle par le patineur : $\sum {\overrightarrow {Forces}} = \overrightarrow F$.
Représenter $\sum {\overrightarrow {Forces}} = \overrightarrow F$ sur le schéma en M2 et M10.
• Comparer les directions et les sens des vecteurs $\overrightarrow {Forces} \ et \ \overrightarrow {\Delta v}$
• Indiquer les caractéristiques du vecteur dans le cas où les forces exercées ne se compensent pas : $\sum {\overrightarrow {Forces}} \neq \overrightarrow 0$
EXERCICES : 9 ; 10 ; 11 ; 13 ; 14 ; 18 ; 20 ; 27 ; 29 ; 34 ; 35 P 231 à 237
COURS
C1.Référentiel d'étude.
C11.Notion de référentiel.
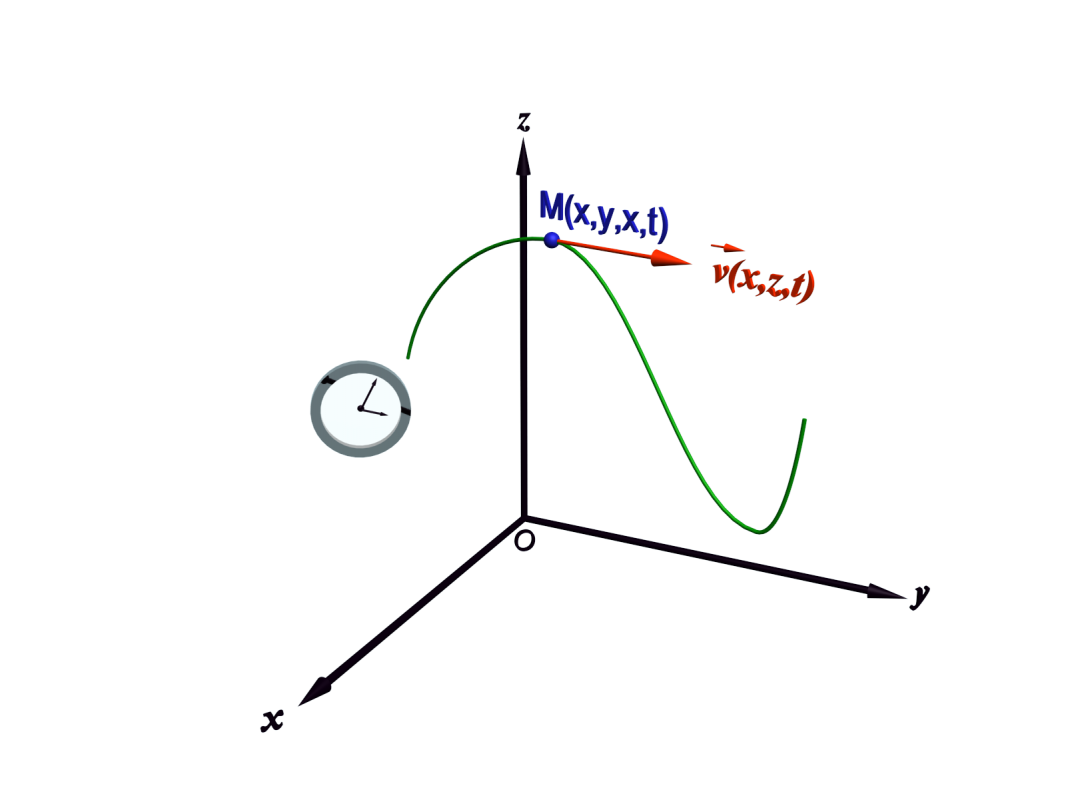 |
Un référentiel est un objet par rapport auquel on étudie le mouvement d'un système. Il est muni d'un repère et d'une échelle de temps.
• Le référentiel terrestre, lié à la Terre est adapté à l'étude du mouvement d'un objet proche de la Terre. • Les référentiels astrocentriques sont liés au centre d'un astre et associés à des axes de directions fixes par rapport à des étoiles lointaines |
| Référentiel Géocentrique : | 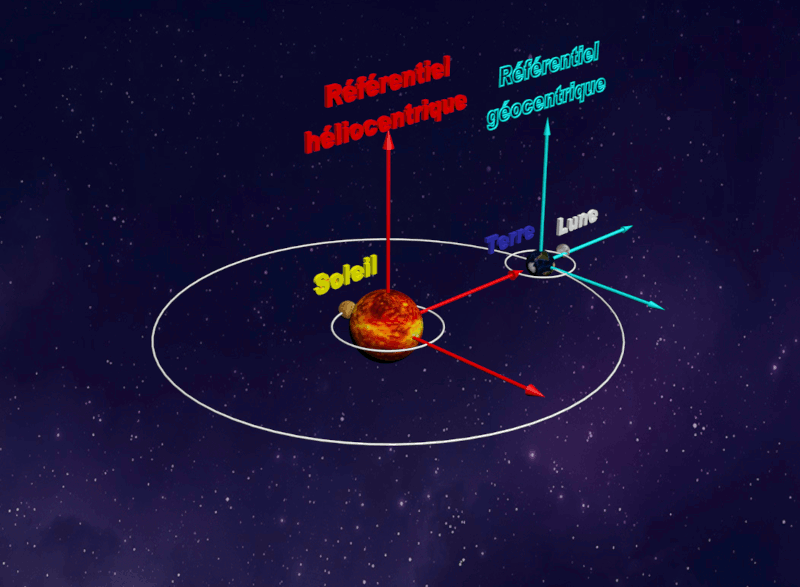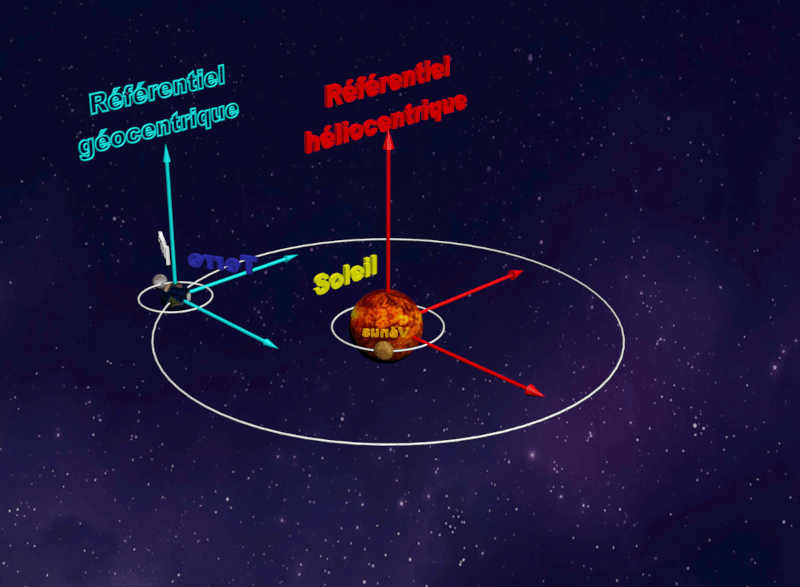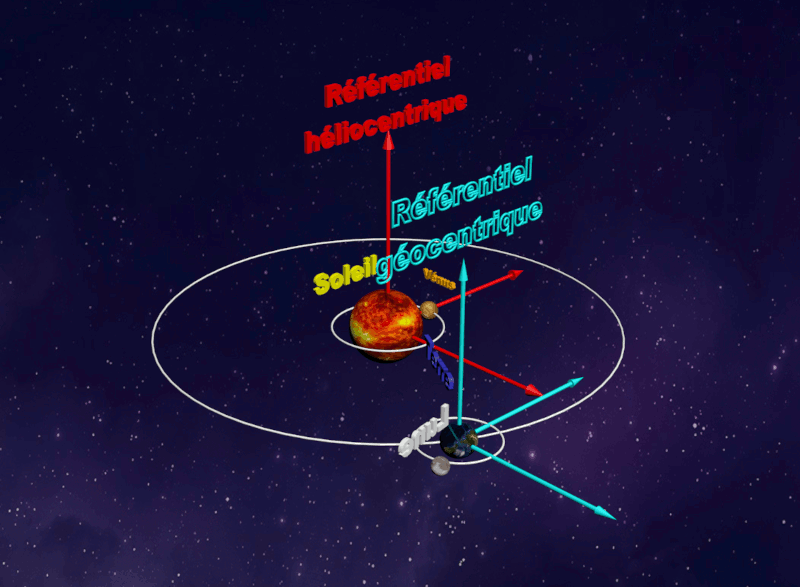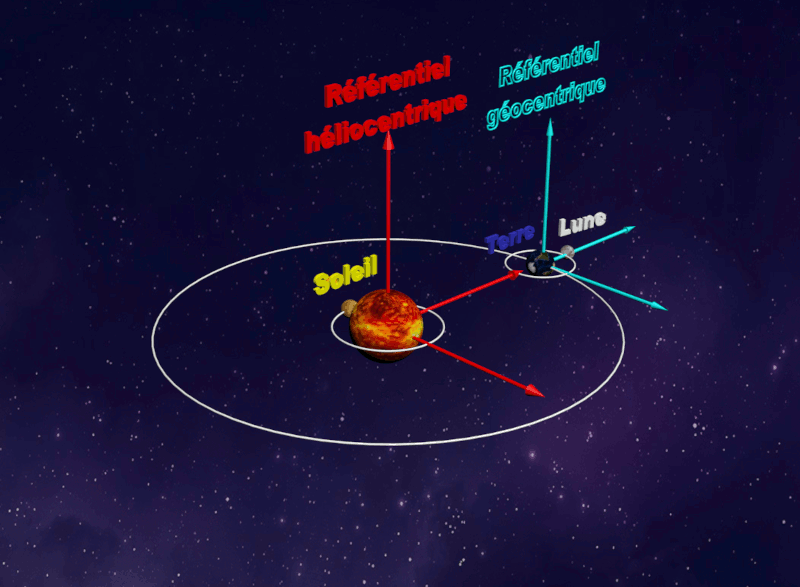 |
|
Référentiel Terrestre : |
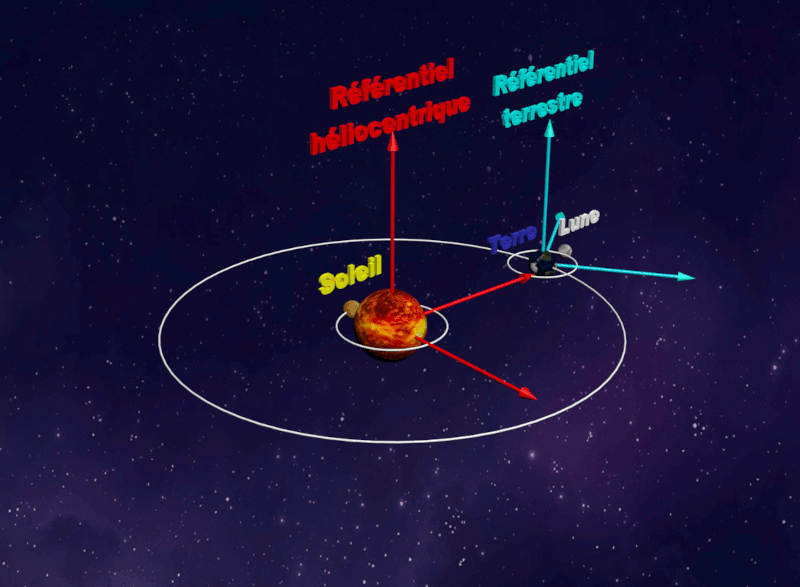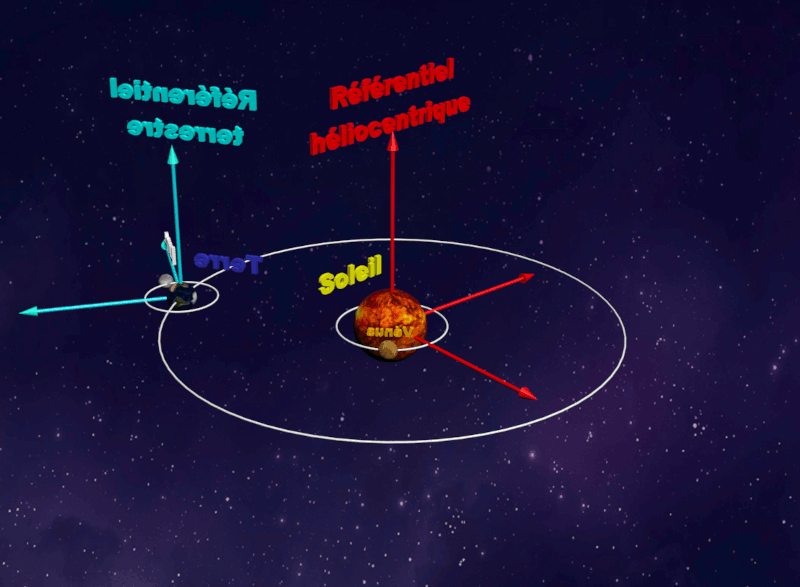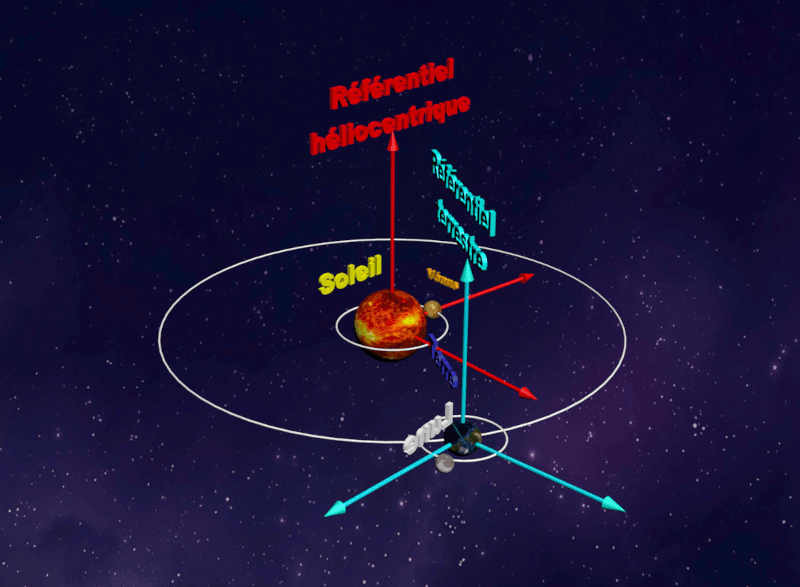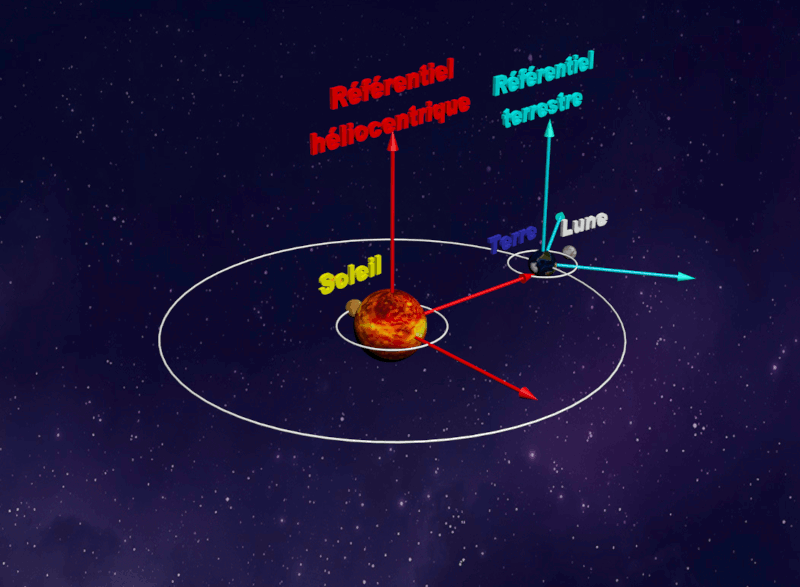 |
C12. Repère.
|
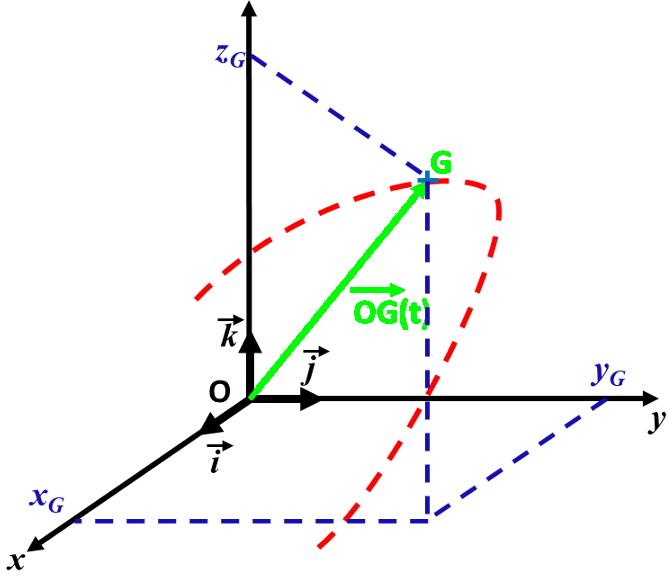
• Le repère cartésien $ \left ( O ; \vec i ; \vec j ;\vec k \right ) $ a pour origine le point O et pour vecteurs unitaires constants $ \left ( \vec i ; \vec j ;\vec k \right ) $. |
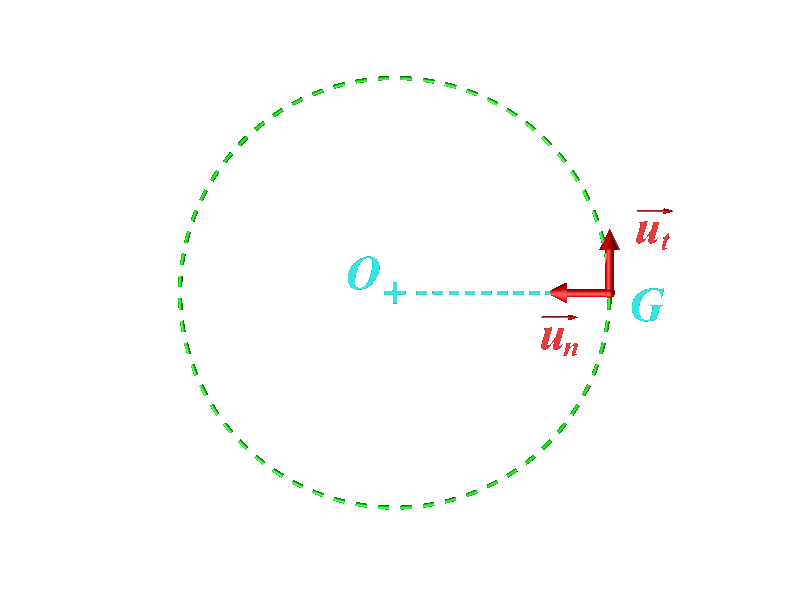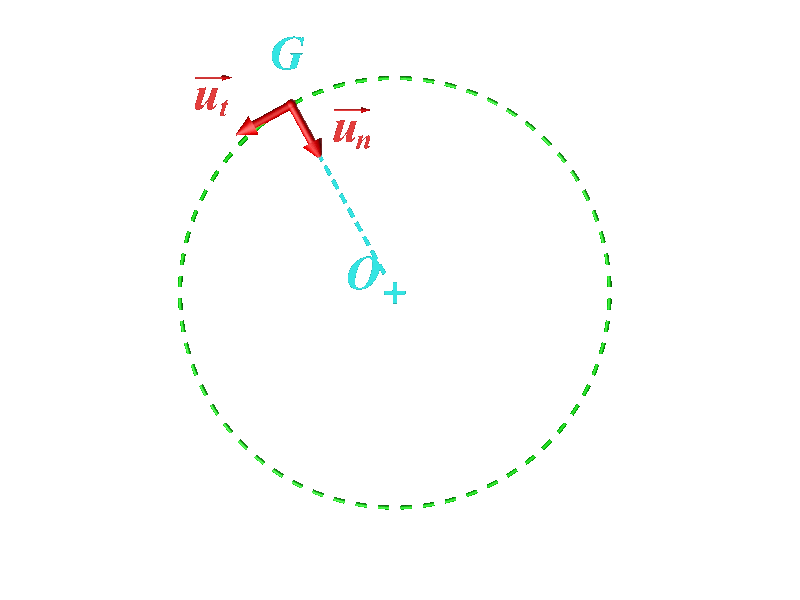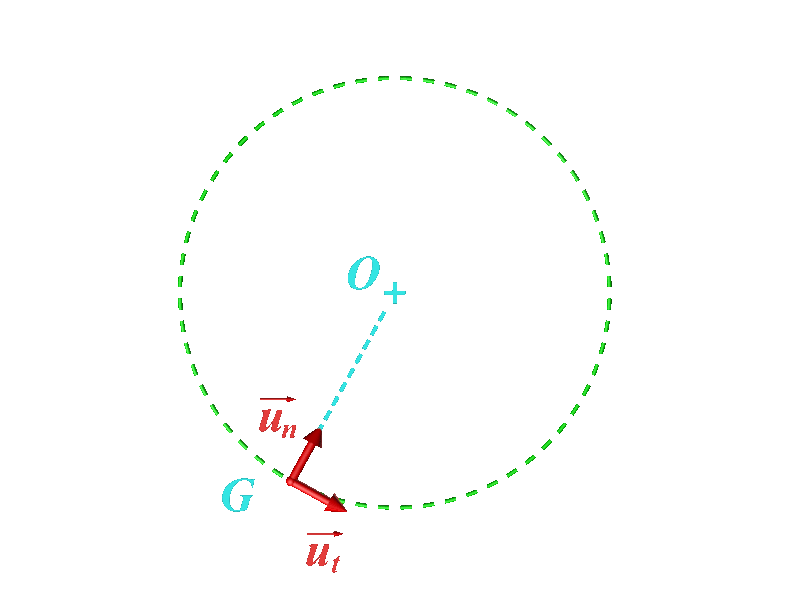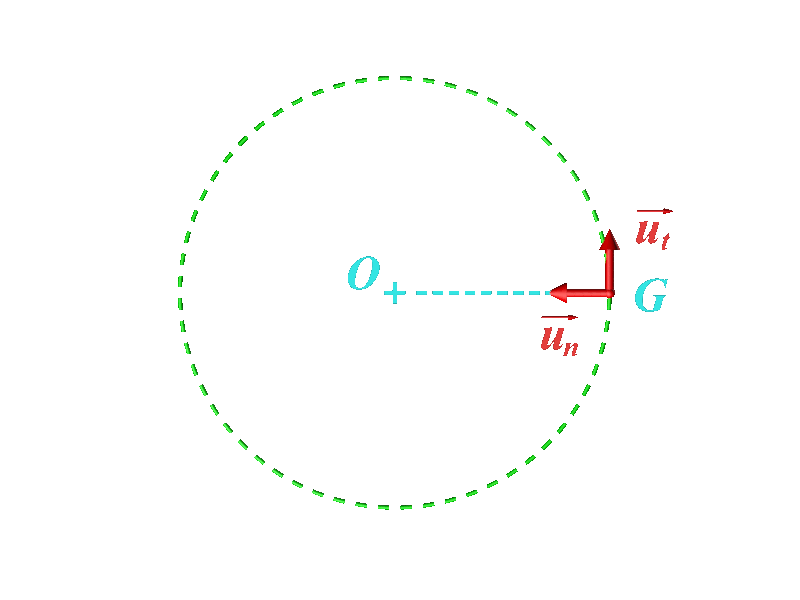
• Le repère de Frenet a pour origine le point G en mouvement. Ses vecteurs unitaires sont : •$\overrightarrow {u_t}$ : tangent à la trajectoire, dans le sens du mouvement. $\overrightarrow {u_n}$ : orthogonal à $\overrightarrow {u_t}$ et vers l'intérieur de la trajectoire. |
C2. Le vecteur vitesse.
C20 Trajectoire.
 |
Lors du déplacement d'un mobile, la trajectoire de ce mobile est la courbe reliant ses positions successives. |
C21 Norme du vecteur vitesse.
|
Le système est considéré comme ponctuel (pour un système non ponctuel, il sera ramené à son centre de gravité).
La vitesse instantanée vi de la vitesse dans la position Mi est assimilée à la valeur de la vitesse moyenne du système entre deux positions très proches Mi et Mi+1 : $v_i = \dfrac {M_iM_{i+1}}{t_{i+1}-t_i}$
MiMi+1 : longueur du segment [Mi Mi+1], en m. ti+1 - ti : durée du parcours entre ces deux points. |
 |
C22. Caractéristiques du vecteur vitesse.
|
Le vecteur vitesse $\overrightarrow v$ en un point de la trajectoire est assimilé au vecteur vitesse moyenne obtenu pour une durée extrêmement courte : $\overrightarrow v_i = \dfrac {\overrightarrow {M_iM_{i+1}}}{t_{i+1}-t_i}$
Le vecteur vitesse $\overrightarrow v $ est défini par :
|
 |
C3. Le vecteur variation de vitesse.
Lors d'un mouvement, le vecteur vitesse $\overrightarrow v$ peut varier, en direction, en sens et en norme.
Le vecteur variation de vitesse $\overrightarrow {\Delta v} $ entre deux positions successives est défini par :
$\overrightarrow {\Delta v} = \overrightarrow {v_{i+1}}-\overrightarrow {v_{i}}$
C4. Somme des forces appliquées au système.
|
Dans un référentiel galiléen, pour un système de masse constante soumis à une ou plusieurs forces, son vecteur variation de vitesse $\overrightarrow {\Delta v} $ pendant une durée extrêmement courte a pour expression : $ \sum {\overrightarrow {F_{ext}}} = m \frac {\overrightarrow {\Delta v}}{dt} $
$ \sum {\overrightarrow {F_{ext}}}$ : somme des forces extérieures appliquées (exprimée en Newton) pendant la durée Dt (exprimée en seconde). |
|
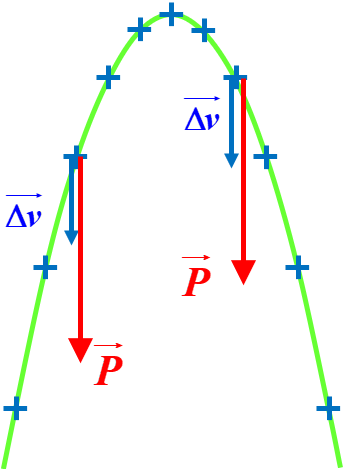
Mouvement de chute libre : La somme des forces est égale au poids de l'objet. Le vecteur variation de vitesse et le vecteur poids sont verticaux, orientés vers le bas. |
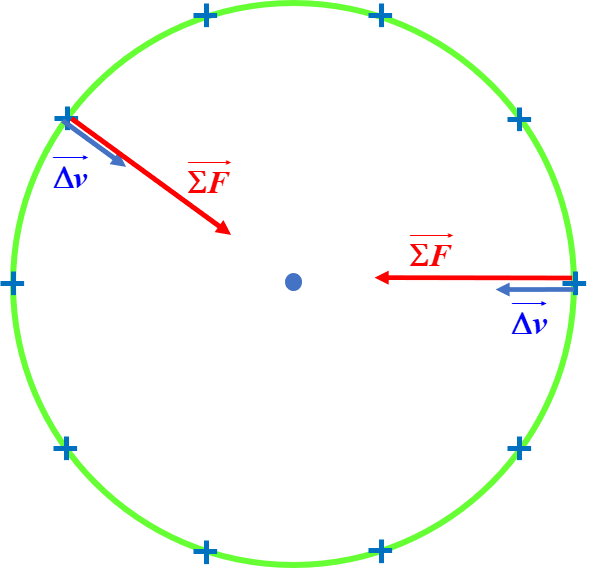
Mouvement circulaire uniforme : La somme des forces et le vecteur vitesse sont centripètes (dirigés vers le centre de la trajectoire). |
Commentaires
-

- 1. LEFEBVRE William Le 06/03/2025
Bonjour, ce chapitre est plutot compliqué mais bien expliqué, merci beaucoup !
Ajouter un commentaire