Mécanique des fluides
A1. La poussée d'Archimède.
|
Sur toutes les mers du monde, différentes indications du niveau de flottaison sont visibles sur la coque des bateaux. |
 |
Pourquoi n’y a-t-il pas un niveau de flottaison unique ?
|
|
|
|
Réaliser.
$\bullet$ Mettre en œuvre le protocole avec de l'eau salée, de l'éthanol ou de l'eau.
$\bullet$ En appliquant le principe d'inertie et à l'aide de la manipulation et du doc 2, déduire la direction et le sens de la poussée d'Archimède.
$\bullet$ À l'aide d'un tableur tracer $P \ - \ P_{apparent} \ = \ f \left( V \times \ g \right)$.
Valider.
$\bullet$ Dans le cadre de l'eau salée, comparer la valeur de la densité obtenue expérimentalement avec la valeur attendue. Commenter.
Analyser.
Donner l'expression vectorielle de la poussée d'Archimède et justifier la nécessité des indications de flottaison sur la coque des bateaux.
A2. Étude qualitative et quantitative de l'écoulement d'un fluide incompressible en régime permanent.
Un quart des décès liés au tabagisme sont causés par une maladie cardiovasculaire.
Comment la circulation du sang est-elle modifiée en cas d'obstruction d'un vaisseau sanguin ?
|
|
|
S’approprier.
Calculer le débit volumique $D_v$ dans l’artère, en $L.min^{ \ -1}$.
Analyser-raisonner
$\bullet$ Déduire de la conservation du débit sanguin l’effet d’une plaque d’athérome sur la vitesse du sang au niveau de la plaque.
$\bullet$ Juste avant le rétrécissement, la tension $p_A$ est de $16 \ kPa$. Estimer le diamètre $d_R$ au niveau du rétrécissement pour lequel la tension s’annule en supposant le patient allongé.
$\bullet$ En déduire ce qui est observé lorsque $d \ < \ d_R$ et expliquer pourquoi l’athérosclérose à un stade avancé peut être détecté à l’aide d’un stéthoscope.
Valider.
Justifier le principe de Bernoulli : "dans le flux d’un fluide homogène et incompressible soumis uniquement aux forces de pression et de pesanteur, une accélération se produit simultanément avec la diminution de la pression".
Exercices : P 351 à 356
10 ; 12 ; 13 ; 14 ; 15 ; 18 ; 19 ; 20 ; 21 ; 22 ; 23 ; 27 ; 29
COURS
C1. La poussée d'Archimède.
C11. Origine de la poussée d'Archimède.
Considérons :
$\bullet$ Un fluide incompressible au repos dans un référentiel galiléen dans le champ de pesanteur terrestre.
$\bullet$Un solide entièrement immergé dans ce fluide.
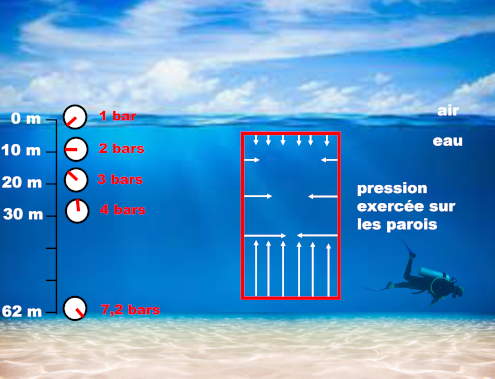
La surface de ce solide est soumise à des forces pressantes de la part du fluide. D'après la loi fondamentale de la statique des fluides, l'intensité des forces pressantes augmente avec la profondeur.
Les forces latérales de compensent alors que la résultante des forces verticales est dirigée vers le haut.
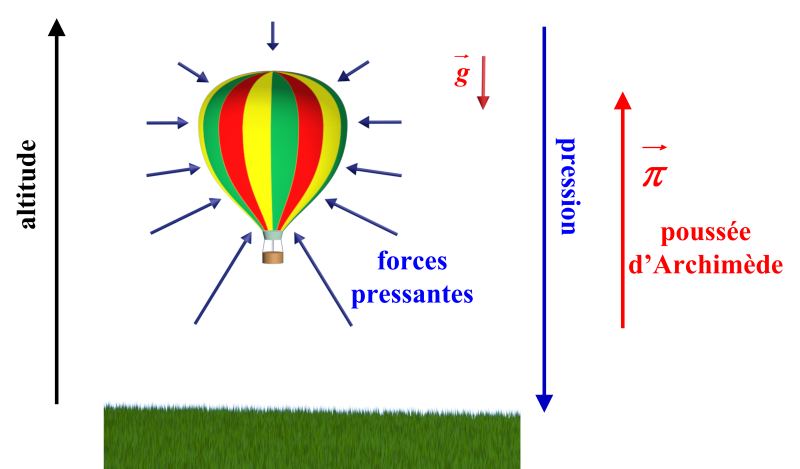
Si le solide est en équilibre, alors il est soumis à une force verticale dirigée vers le haut qui compense son poids $\overrightarrow P$: cette force est la poussée d'Archimède et représente la résultante des forces de pression exercées par le fluide environnant sur le solide.
C12. Expression de la poussée d'Archimède.
C12a. Principe d'Archimède.
|
Tout corps totalement immergé dans un fluide repos et soumis à une force verticale dirigée vers le haut et égale à l'opposé du poids de volume déplacé. |
|
La poussée d'Archimède notée $\color{red}{\overrightarrow \pi}$ a pour caractéristiques : $\bullet$ Verticale. $\bullet$ Vers le haut. $\bullet$ De norme : $\color{red}{\pi \ = \ m_{fluide} \times g \ = \ \rho_fluide \times V_{fluide} \times g}$ $\rho_{fluide}$ : masse volumique du fluide $\left ( kg.m^{ \ -3} \right )$ $V_{fluide}$ : volume de fluide déplacé $\left (m^{ \ 3} \right )$ $g$ : intensité de la pesanteur $\left ( m.s^{ \ -2} \right )$ |
 |
Remarque :
$\overrightarrow \pi \ = \ - \overrightarrow P_{fluide} \ = \ - \ m_{fluide} \times \overrightarrow g \ = \ - \rho_{fluide} \times \ V_{fluide} \times \overrightarrow g$
C12b. Condition de flottaison dans un fluide.
On considère un solide partiellement immergé flottant à la surface d'un liquide.
Celui-ci, se trouve immergé dans deux fluides : le liquide et l'air.
Il est donc soumis à deux poussées d'Archimède. Celle exercée par le liquide et celle exercée par le liquide.
La masse volumique de l'air étant négligeable devant celle du liquide, seule la poussée exercée par le liquide sera considérée.
Le solide sera en équilibre à la surface du liquide si son poids est compensé par la poussée d'Archimède exercée sur le seul volume de solide immergé.
 |
Le solide de volume $V$ a coulé. Il est soumis à son poids, la poussée d'Archimède et la réaction du fond : $\overrightarrow \pi \ + \ \overrightarrow P \ + \ \overrightarrow R \ = \ \overrightarrow 0$ $- \rho_{fluide} \times V \times \overrightarrow g \ + \ m \times \overrightarrow g + \ \overrightarrow R \ = \ \overrightarrow 0$ $\left ( m - \rho_{fluide} \times V \right ) \ \times \overrightarrow g \ + \ \overrightarrow R \ = \ \overrightarrow 0$ |
 |
Le solide volume $V$ est en suspension. Il est soumis à son poids, la poussée d'Archimède : $\overrightarrow \pi \ + \ \overrightarrow P \ = \ \overrightarrow 0$ $- \rho_{fluide} \times V \times \overrightarrow g \ + \ m \times \overrightarrow g \ = \ \overrightarrow 0$ $\left ( m - \rho_{fluide} \times V \right ) \ \times \overrightarrow g \ = \ \overrightarrow 0$ |
 |
Le solide volume $V$ flotte. Seul un volume $V'$ est immergé. Il est soumis à son poids, et à la poussée d'Archimède de la seule partie immergée. $\overrightarrow \pi_{immergé} \ + \ \overrightarrow P \ = \ \overrightarrow 0$ $- \rho_{fluide} \times V' \times \overrightarrow g \ + \ m \times \overrightarrow g \ = \ \overrightarrow 0$ $\left ( m - \rho_{fluide} \times V' \right ) \ \times \overrightarrow g \ = \ \overrightarrow 0$ |
C2. Fluide en écoulement.
C20. Hypothèses.
$\bullet$ On considèrera un fluide parfait, non visqueux (les forces de frottements sont négligées).
$\bullet$ On considèrera un fluide homogène et incompressible.
$\bullet$ L'écoulement est non tourbillonnant.
$\bullet$ L'écoulement est considéré en régime permanent ou stationnaire : la vitesse et la pression en tout point sont indépendantes du temps.
C21. Débit volumique.
C21a. Définition.
|
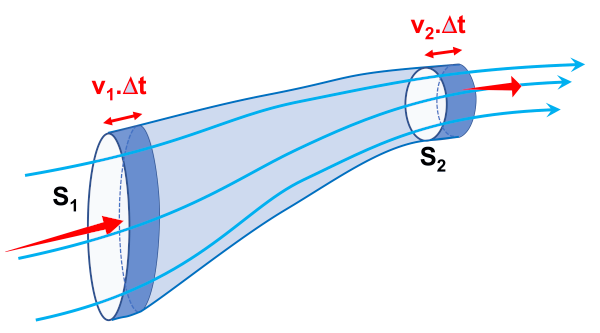
Le débit volumique est le volume de fluide qui s'écoule par unité de temps à travers une section droite S de la conduite qui délimite le mouvement du fluide. $\color{red}{D_v \ = \ S \times v}$ $D_v$ : débit volumique $\left ( m^{ \ 3}.s^{ \ -1} \right )$. $S$ : surface de la section $\left ( m^{ \ 2} \right )$. $v$ : vitesse découlement $\left ( m.s^{ \ -1} \right )$. |
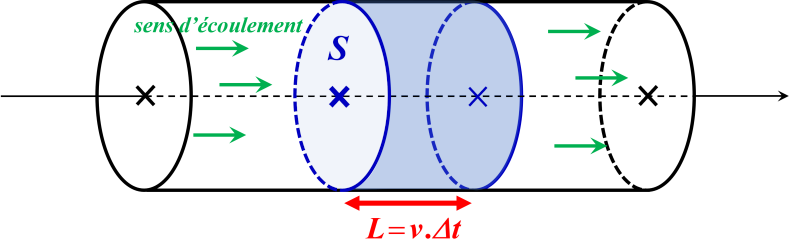
Le volume $V$ de fluide s'écoulant pendant un intervalle de temps $\Delta t$ est : $V \ = \ S \times L$.
Le fluide s'écoulant à la vitesse $v$, la distance $L$ parcourue pendant $\Delta t$ est : $L \ = \ v \times \Delta t$.
Le volume de fluide déplacé (débit volumique), $D_v \ = \ \dfrac{V}{\Delta t}$ est bien : $D_v \ = \ \dfrac{V}{\Delta t} \ = \ \dfrac{S \times L}{\Delta t} \ = \ \dfrac{S \times v \times \Delta t}{\Delta t} \ = \ S \times v$
C21b. Conservation de la masse et du débit volumique.
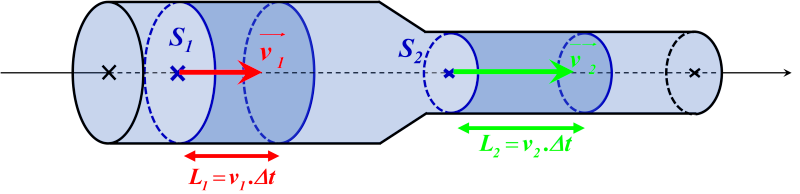
Dans le cas fluide incompressible s'écoulant dans une conduite de section variable : le volume s'écoulant est indépendant de la durée $\Delta t$ d'écoulement.
$D_1 \ = \ D_2$
$\Leftrightarrow \ \ S_1 \times \ v_1 \ = \ S_2 \times \ v_2$
$\Leftrightarrow \ \ \dfrac{v_1}{v_2} \ = \ \dfrac{S_2}{S_1}$
Ainsi :
$\bullet$ si la section diminue : $\dfrac{S_2}{S_1} \ > \ 1 \ \Leftrightarrow \ = \ \dfrac{v_1}{v_2} \ > \ 1$ : la vitesse augmente.
$\bullet$ si la section augmente : $\dfrac{S_2}{S_1} \ < \ 1 \ \Leftrightarrow \ = \ \dfrac{v_1}{v_2} \ < \ 1$ : la vitesse diminue.
C3. Relation de Bernoulli.
Lors de l'écoulement d'un fluide dans une conduite d'altitude variable, en tout point du fluide :
$\color{red}{\dfrac{\rho v^{ \ 2}}{2} \ + \ \rho gz \ + \ p \ = \\dfrac{\rho v^{ \ 2}}{2} \ + \ \rho gz \ + \ p \ = \ constante}$
$\rho$ : masse volumique du fluide $\left ( kg.m^{ \ -3} \right )$.
$v$ : vitesse d'écoulement $\left ( m.s^{ \ -1} \right )$.
$z$ : altitude $\left ( m \right )$.
$p$ : pression $\left ( Pa \right )$.
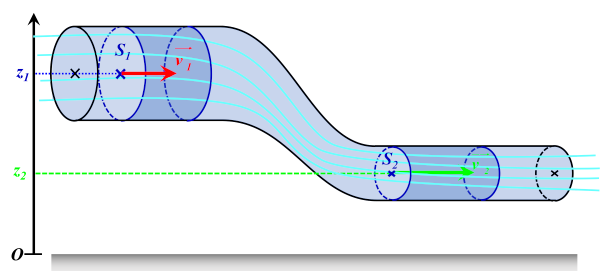
NB :
Dans le cas d'un fluide au repos, la relation s'écrit :
$\color{red}{ \rho gz \ + \ p \ = \ constante}$
Loi fondamentale de la statique des fluides.
C4. Effet Venturi.
Dans le cas d'une conduite horizontale ($z_1 \ = \ z_2 \ = \ z$) possédant un étranglement ($S_1 > S_2$)

La conservation du débit s'écrit : $D_1 \ = \D_2 \ \Leftrightarrow \ S_1 \times v_1 \ = \S_2 \times v_2$
Alors : $v_2 \ = \ \dfrac{ S_1}{ S_2} \times v_1$
En reportant dans la relation de Bernoulli :
$\dfrac{\rho v_1^{ \ 2}}{2} \ + \ \rho gz \ + \ p_1 \ = \ \dfrac{\rho v_2^{ \ 2}}{2} \ + \ \rho gz \ + \ p_2$
$\Leftrightarrow \dfrac{\rho v_1^{ \ 2}}{2} \ + \ \rho gz \ + \ p_1 \ = \ \dfrac{\rho}{2} \left ( \dfrac{ S_1}{ S_2} \times v_1 \right )^{ \ 2} \ + \ \rho gz \ + \ p_2$
$p_2 \ = \ p_1 + \ \dfrac{\rho}{2} \times v_1^2 \left ( 1\ - \ \left (\dfrac{ S_1}{ S_2} \right ) ^2 \right )$
Comme $S_1 \ > \ S_2$, $\dfrac{ S_1}{ S_2} > 1$ on a : $1 \ - \ \left( \dfrac{ S_1}{ S_2} \right )^2 \ < \ 0$
Et donc : $p_2 > p_1$
Lors de la diminution de la section, la pression augmente.
La vitesse augmente au niveau de l'étranglement.
Ajouter un commentaire