Mouvement dans un Champ de Gravitation

ACTIVITES

A1 : Histoire.

La conquête spatiale n'a pas eu lieu avec l'envoi des premiers satellites. Elle a débuté avec l'observation du ciel.

Objectif : Etablir les repères historiques concernant la mécanique céleste et les satellites.

Doc1 : Trombinoscope.

Trombino

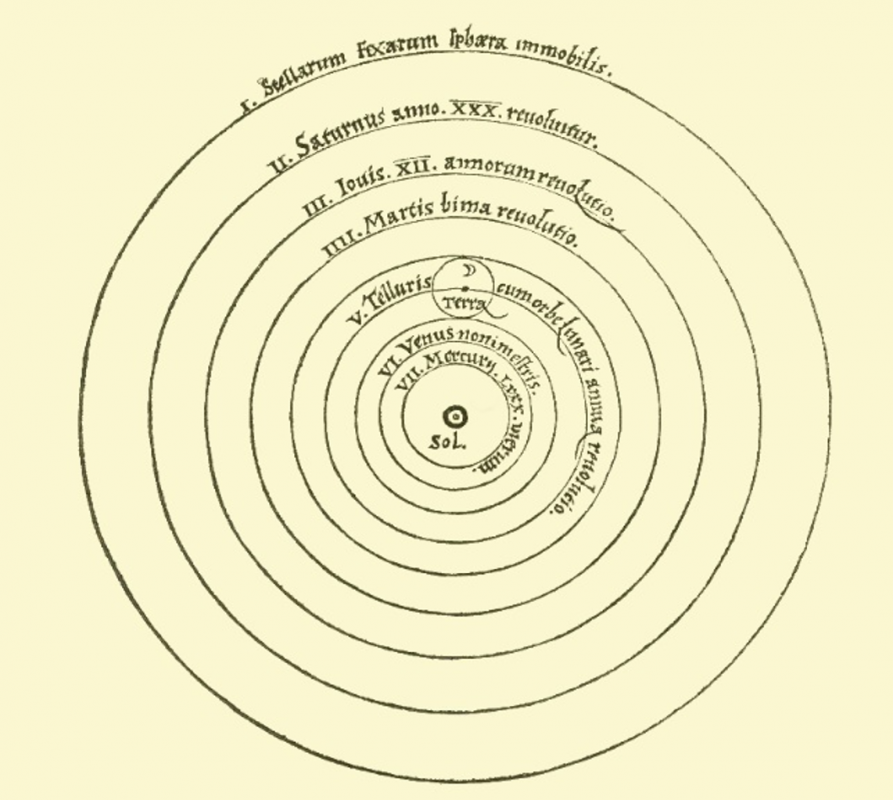
Doc2 : Le système de Copernic.

Syst copernic

Doc3 : Ecrits.

"De revelutionus orbitum cemlenusé : Copernic

"Astronomia Nova" : Kepler

"Dialogo sopra due massimi sistemi del mond" : Galilée

"De la Terre à la Lune" : Jules Verne

"Objectif Lune, On a marché sur la Lune." :Hergé

Doc4 : Dans l'ordre.

· Détermination distance Terre Lune.

· Observation des satellites de Jupiter.

· Dessin précis des anneaux de Saturne

· Pose d’un pied humain sur la Lune.

· Envoi sonde en dehors du système solaire.

· Exploration planète par robot

· Arrimage objet sur une comète.

Questions :

• Pour chaque savant du doc1, rechercher nationalité, dates de naissance et mort et donner des indications sur ses apports à la connaissance du mouvement des planètes. Pour ce faire on réalisera une frise.

• Attribuer les noms français aux astres de chaque orbite du doc2.

• Rechercher ce qu'est le système de Ptolémée.

• Quelles erreurs peut-on constater à partir de vos connaissances à partir du doc2.

• Pour chaque livre du doc3, chercher leurs dates de parution et dire en quoi il a pu être novateur.

• Rechercher les dates et les auteurs des évènements cités dans le doc4.

Synthèse :

D'après vous, quelles sont les dates les plus importantes des découvertes effectuées ? Argumenter.

A2 : Orbite de Mercure.

Dans cette activité, on se propose de vérifier la première loi de Kepler en utilisant un simulateur d'orbite créé par à l'aide de Python.

Doc1 : Simulateur d'orbite.

# -*- coding: utf-8 -*-
from matplotlib import*
from numpy import*
from pylab import *
import math as m
import scipy.optimize as op

t=[]
M=[]
u=[]
theta=[]
R=[]
X=[]
Y=[]

T_rev=0.240 #pérode de révolution en annnée#
e=0.206 #excenticité#
a=0.387 #1/2 gd axe#
N=40 #nbre de positions"

for i in range (N):
t.append(i*T_rev/N)
M.append(2*m.pi/T_rev*t[i])
u.append(float(op.fsolve(lambda x:x-e*sin(x)-M[i],0)))
theta.append(2*m.atan((m.sqrt(1+e)/(1-e)*m.tan(u[i]/2))))
R.append(a*(1+e**2)/(1+e*m.cos(theta[i])))
X.append(R[i]*m.cos(theta[i]))
Y.append(R[i]*m.sin(theta[i]))

plt.grid(True)
plt.xlabel("distance (U.A)")
plt.ylabel("distance (U.A)")
plt.axis('equal')
plt.plot(X,Y,"bo")
plt.plot(0,0,"go")
plt.show()

Doc 2 : Caractéristque d'une orbite elliptique.

Les orbites des planètes autour du soleil ne sont pas des cercles mais des ellipses. Un cercle est caractérisé par son centre C et son rayon R tandis qu'une ellipse est caractérisée par son centre O, son demi grand axe a, ces deux foyers F et F' et son excentricité e = c/a où c = OF = OF'. Le Soleil occupe l'un des deux foyers de cette ellipse. La position de la planète au plus proche du soleil est appelé périhélie et l'aphélie le point le plus lointain.

Cercle 1

Ellipse

Doc3 : Données planétaires.

Planète	a(UA)	T(an)	e
Mercure	0,387	0,240	0,206
Vénus	0,723	0,615	0,007
Terre	1,00	1,00	0,017
Mars	1,52	1,80	0,093
Jupiter	5,20	11,9	0,048
Saturne	9,54	29,4	0,054
Uranus	19,2	84,0	0,046
Neptune	30,0	165	0,010

UA : l'unité astronomique elle conseille elle correspond à la distance moyenne de la Terre au Soleil soit 150 millions de kilomètres.

• Dans quel référentiel supposé galiléen est représentée son orbite ?

• A quelle distance du soleil se trouve l'aphélie de Mercure ? son périhélie ?

• En utilisant la représentation obtenue par la simulation déterminer la vitesse à l'aphélie et au périhélie de Mercure.

• En faisant évoluer le programme on peut déterminer les planètes dont l'orbite est proche d'un cercle pour cela il suffit de changer les valeurs (demi-grand axe, excentricité, période de révolution) des différentes planètes dans le code point. On peut aussi modifier le nombre N de positions affichées.

• Dans ce cas de quelle valeur est proche l'excentricité e ?

• Donner les noms des planètes concernées.

• Que peut-on dire de la vitesse de ces planètes ?

• Représenter sur un schéma quelques valeurs de vitesse et accélération de la planète étudiée :

- Mercure.

- Dans le cas d'une planète ayant une orbite quasi circulaire.

A3. Deuxième loi de Kepler.

Aucun objet céleste n'est observé en permanence pour en déterminer la position. A l'aide d'observations ponctuelles et des lois de la mécanique on peut cependant calculer la position en temps réel de chaque objet.

Objectif : exploiter des données satellitaires pour tester la 2^nde loi de Kepler.

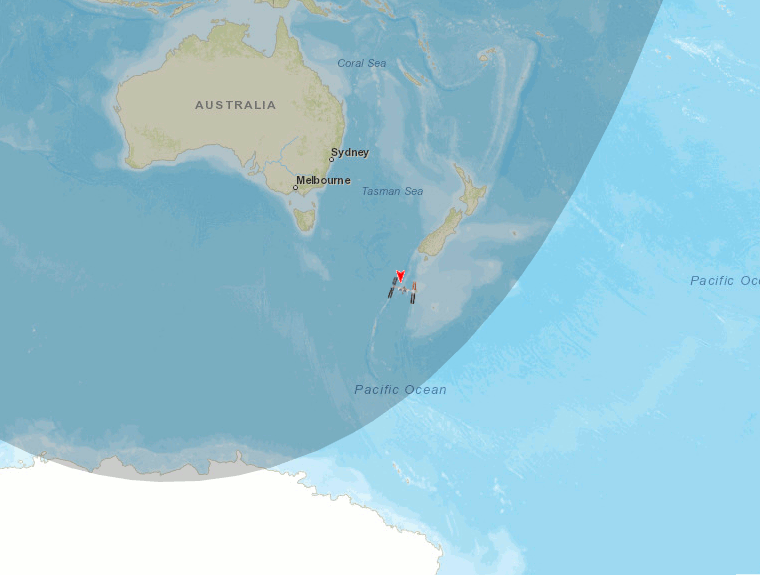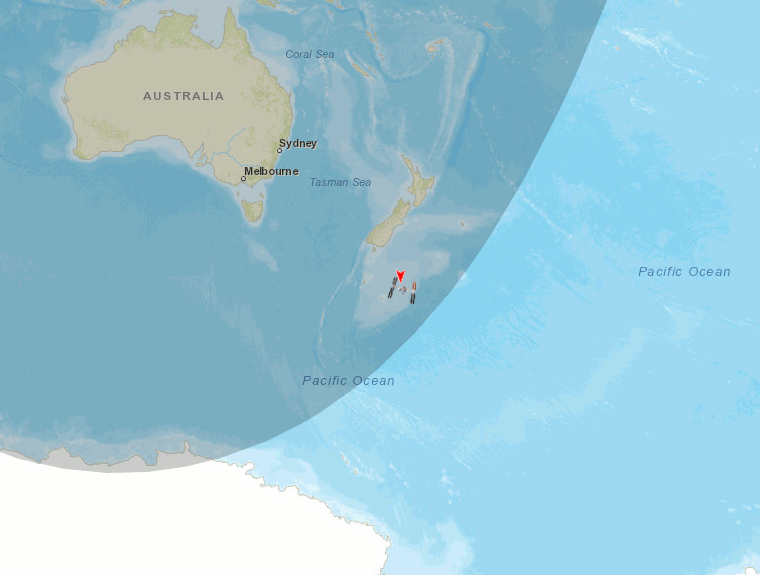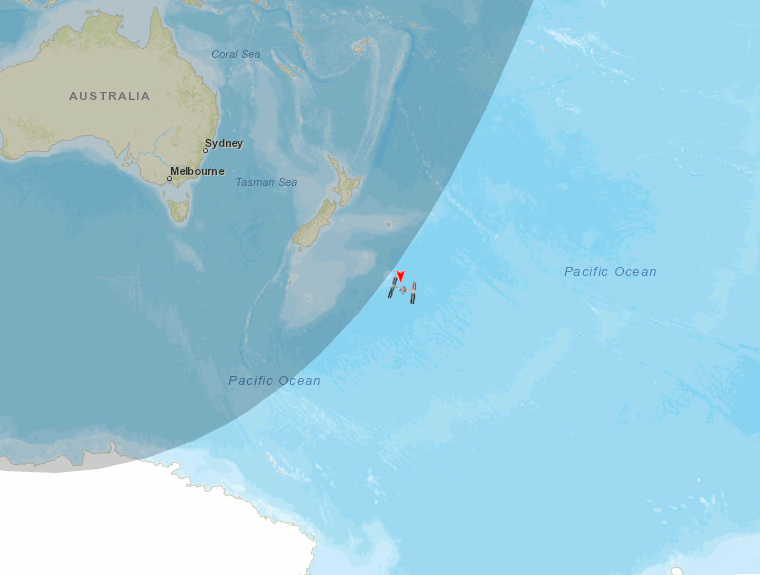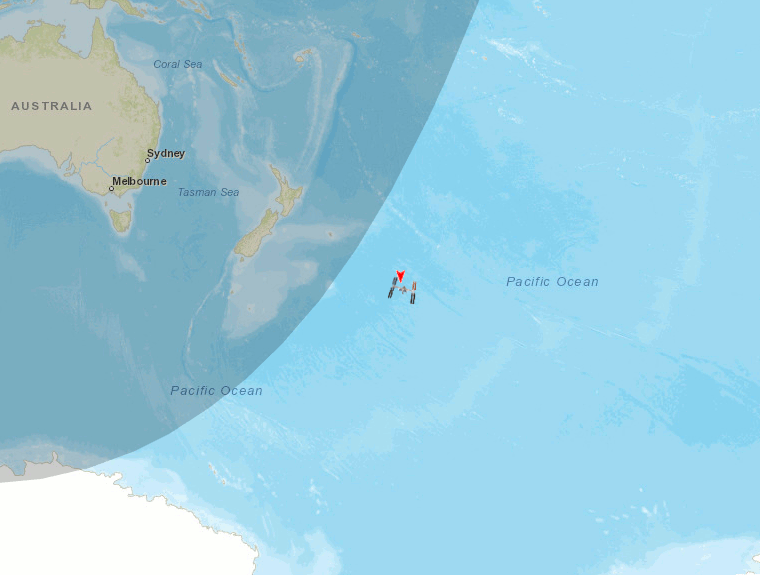
Doc1 : Suivre un satellite en temps réel.

La plupart des satellites terrestres font l'objet d'une surveillance. Leur position effective est mesurée régulièrement ce qui permet de calculer leur position à tout instant le site www.n2yo.com donne les données d'un satellite dans le ciel : latitude (LAT) et longitude (LNG) en degrés et l'altitude (ALT) au-dessus du sol et en kilomètres. Une capture d'écran permet d'avoir à un instant donné les coordonnées du satellite.

Doc2 : satellites à suivre.

La liste ci-contre contient des satellites terrestres ayant une orbite aplatie et une période orbitale de quelques heures cela permet de tester la 2^ème loi de Kepler pendant une séance de TP

• Spirale A : surveillance de missiles, armée française lancé en 2009

• Tacsat 4 : communication Marine américaine lancée en 2011

• Express MD2 : satellite de communication russe dont le lancement a échoué et placé sur une mauvaise orbite lancée en 2012

• DSX : recherche armée de l'air américaine lancée en 2010

• Podsat : mission secrète armée américaine lancée en 2018

• Akebono : satellite japonais de recherche lancé en 1989

Doc3 : Formule de Héron d'Alexandrie.

L'aire S d'un triangle quelconque dont les côtés ont pour longueur a, b et c s'obtient par la relation :

Triangle 1

$ S = \sqrt {p \left ( p-a \right )\left ( p-b \right )\left ( p-c \right )} $

où p et le demi-périmètre du triangle.

Doc4 : Aire balayée.

Soit T le centre de la terre et M un satellite de la terre.

• L'aire balayée par le segment [TM] entre les instants t₁ et t₂ et environ l'aire du triangle TM(t₁)M(t₂).

• L'aire balayée par l'unité le temps est :

$ s =\dfrac {S}{t_{2}-t_{2}} $

(on parle de vitesse aréolaire)

Aire balayee

TP à rédiger et à rendre en fin de séance.

Etude :

• Pendant 30 minutes relever toutes les 5 minutes, l’instant t, la latitude et la longitude et l’altitude du satellite. (Répondre aux questions suivantes pendant le relevé des valeurs)

• Le programme 13_deuxiemeLK_initial.py déduit de ces données les positions x, y et z dans un repère associé au référentiel géocentrique. Compléter le programme pour qu’il calcule :

- La distance entre la position et la position suivante.

- La vitesse du satellite à cette position, dans la liste v ;

- L’aire balayée entre cette position et la position suivant en utilisant les doc 3 et 4 la formule de Héron La vitesse aréolaire à cette position doc 4 dans la liste s.

• Exécuter le programme, traçant le rayon r de l’orbite du satellite, la vitesse v et la vitesse aréolaire s en fonction du temps. Imprimer les courbes et analyser leurs allures (impression écran dans le document).

Etude :

La deuxième loi de Kepler stipule que "Les aires balayées par le rayon-vecteur du centre de l’astre attracteur au centre du satellite sont égales". En quoi les courbes obtenues montrent-elles que la seconde loi est vérifiée ?

A4. Troisième loi de Kepler.

Doc1 : Troisième loi de Kepler.

Soit un astre attracteur de masse M autour duquel des satellites naturels ou artificiels sont en orbite.

Soit T la période de révolution d'un satellite et a le demi-grand axe de son orbite.

La constante gravitationnelle est :

G = 6,67.10^-11 N.m².kg^-2 .

La 3ème loi de Kepler s'écrit :

$ \dfrac {T^2}{a^3} = \dfrac {4\pi^{2}}{GM}$

Doc2 : Astres à tester.

Rendez-vous à l'adresse suivante :

http://www.jf-noblet.fr/planetes/index.htm

Et ici :

http://www.n2yo.com

Rechercher les valeurs de T et a et M, masse de l'astre attracteur.

Doc 3 : Tester la loi par une régression linéaire.

Soit deux grandeurs x et y liées par la loi y = f(x).

Un procédé courant pour tester une cette loi consiste à :

Collecter les mesures de (x ; y) placer les points sur un graphique.
Tracer la courbe-modèle (courbe de régression).
Déterminer son équation et vérifier qu'elle s'écrit bien y = f(x).

On valide ainsi le modèle et les paramètres de la fonction f permettant la détermination de grandeurs physiques.

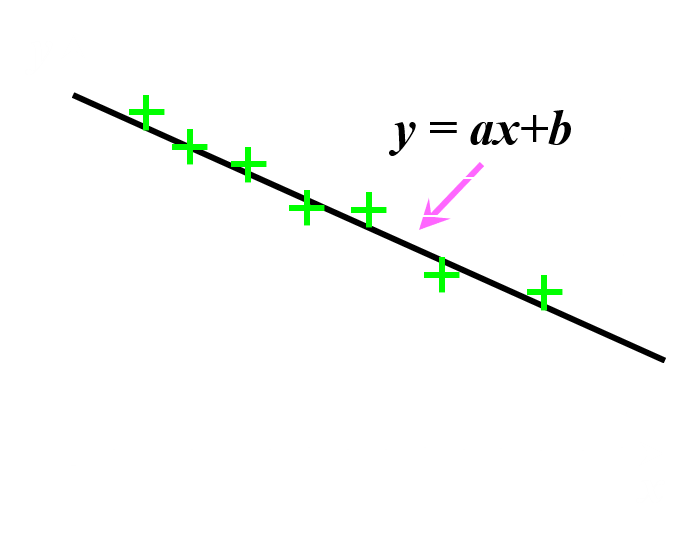
Si la courbe-modèle est une droite, la modélisation s'appelle une régression linéaire. Les paramètres de l'équation sont alors le coefficient directeur a et l'ordonnée à l'origine b de la droite.

Doc 4 : logarithme népérien, rappel.

On rappelle que : $ \ln \left ( a^{n}\right ) = n \times \ ln \left ( a \right ) $ et $ \ln \left ( a\times \ b \right ) = \ln \left ( a \right ) + \ln \left ( b \right ) $

Ainsi lorsque deux x et y grandeurs sont reliées par une relation du type $ \ y^{n} = k \times\ x^{m} $ :

$ n \times\ ln \left ( y\right ) = m \times\ ln \left ( y\right )\ + \ln \left ( k \right ) \Leftrightarrow \ln \left ( y \right ) = \dfrac {m}{n}\times\ ln \left ( x \right ) + b $

La relation liant ln(y) et ln(x) est donc une relation linéaire.

La droite représentant ln(y) en fonction de ln(x) a donc pour coefficient directeur $\frac {m}{n} $. et pour ordonnée à l'origine b.

Analyser.

• Dans le cas de la troisième loi de Kepler, exprimer $ T^{ 2} $ en fonction de $ a^{3} $ (doc1). Conclure.

• Dans le cas de la troisième loi de Kepler, exprimer ln(T) en fonction de ln(a) (doc4). Conclure.

• Donner les avantages de l'utilisation du logarithme népérien.

Réaliser.

• Pour un (des) astre(s) attracteur(s) choisi(s) (doc 2), effectuer l'étude permettant de vérifier la troisième loi de Kepler en utilisant les deux méthodes. Présenter vos résultats.

• Pour chaque méthode, retrouver la valeur de la masse de l'astre attracteur et comparer à la valeur donnée.

Bilan.

• Conclure quant à la méthode la mieux adaptée.

EXERCICES : Pages 327 à 337.

14 ; 15 ; 16 ; 17 ; 18 ; 21 ; 24 ; 26 ; 28 ; 31 ; 34 ; 40

COURS

C1. Cas des mouvements circulaires.

C11. Définition.

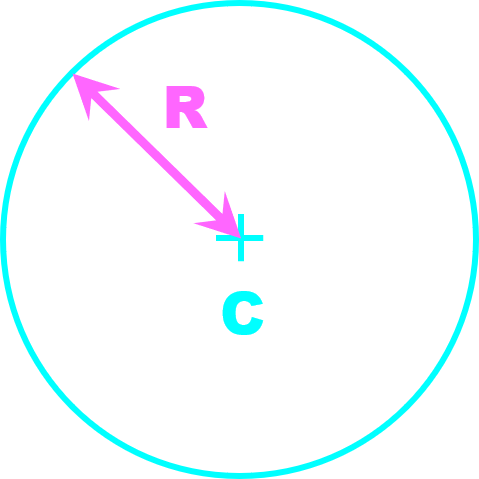
Le mouvement d'un point M est dit circulaire si sa trajectoire est un arc de cercle ou un cercle. Il est uniforme si la valeur v de sa vitesse est constante au cours du temps et accéléré si elle varie.

Soit un point M dont la trajectoire est un cercle de centre O et de rayon R. Le repère de Frenet est le repère d'origine mobiles M(t) et de vecteurs unitaires :

$\overrightarrow {u_t}$ : tangent à la trajectoire, orienté dans le centre du mouvement.

$\overrightarrow {u_n}$ : selon la direction (OM) orienté vers le centre O.

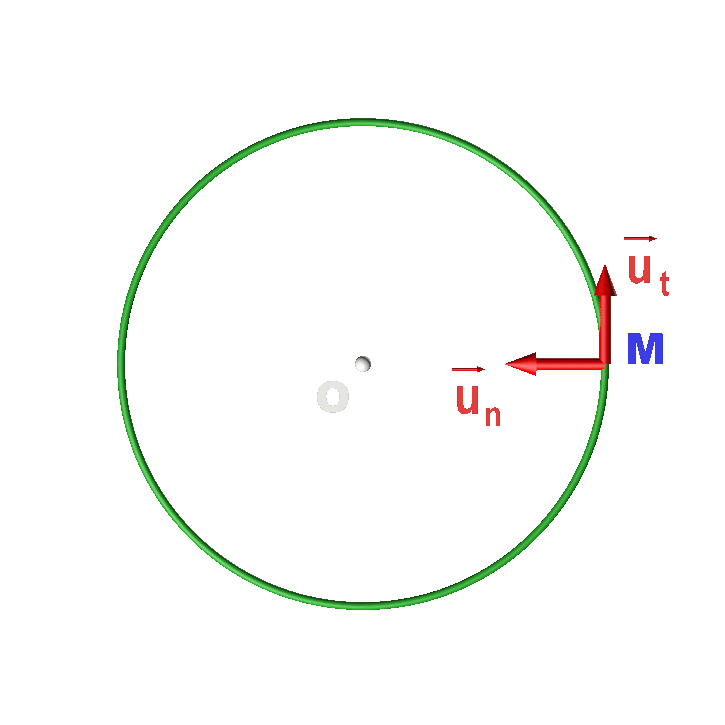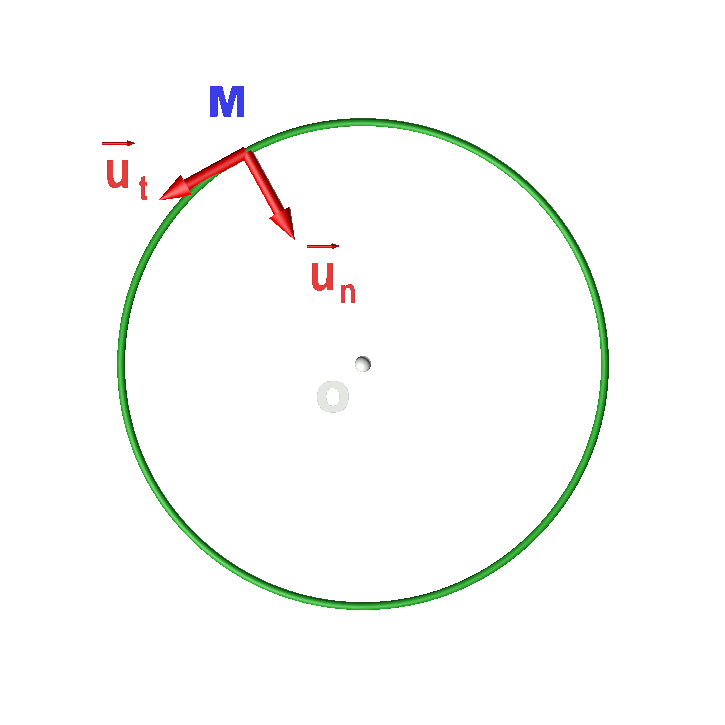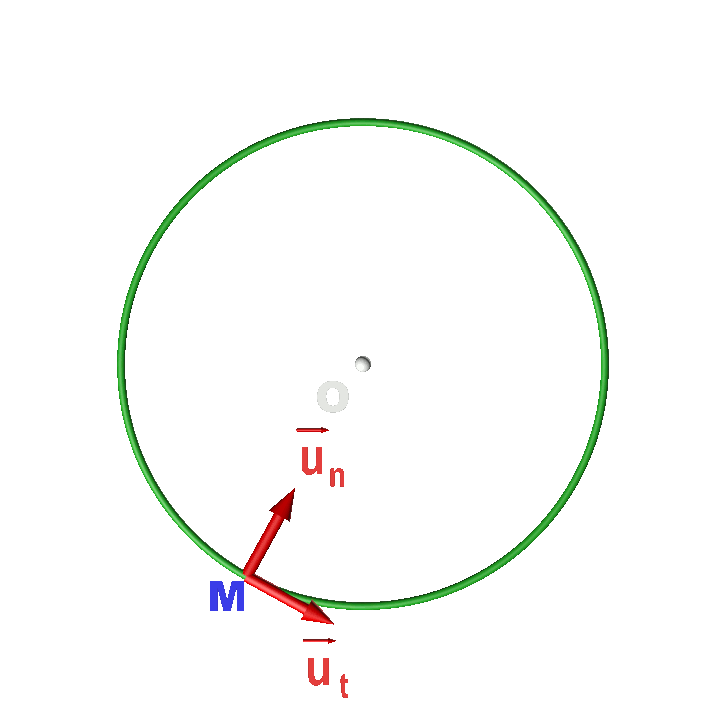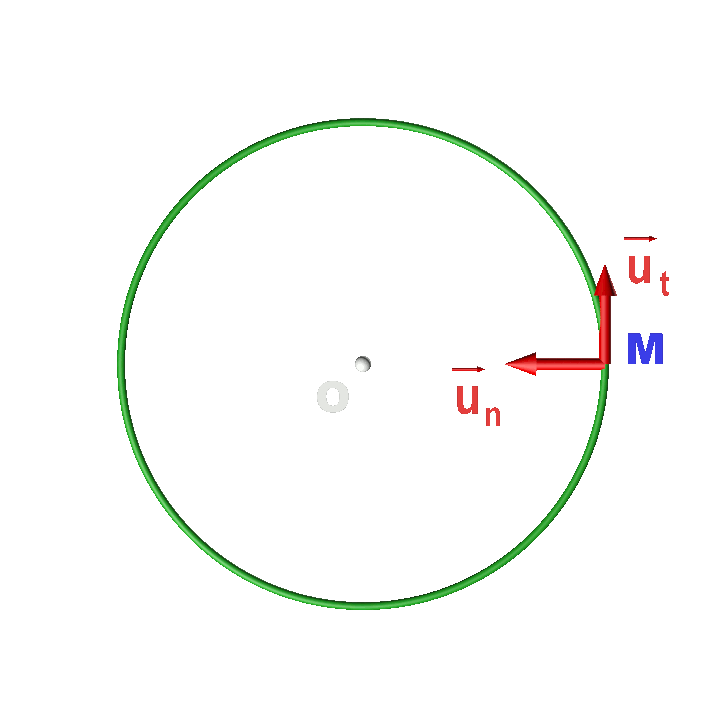C12. Vitesse et accélération dans la base de Frenet

Dans le repère de Frenet en notant v(t) la norme du vecteur vitesse du point M au cours du temps, les coordonnées des vecteurs vitesse v(t) et accélération a(t) du point M en mouvement circulaire sont :

$ \overrightarrow {v_t (t)} =
\begin{pmatrix}
v_t (t)= v(t)\\
v_n (t)= 0
\end{pmatrix} $

(le vecteur vitesse étant tangent à la trajectoire, il n'a pas de composante selon la direction normale)

Donc : $\overrightarrow {v(t)}=v(t) \overrightarrow {u_t}$

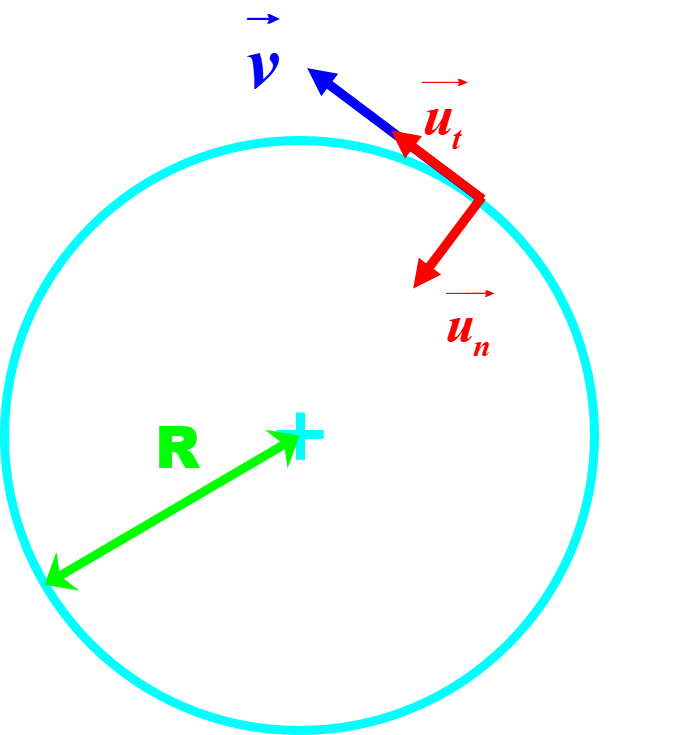$ \vec {a_t (t)} =
\begin{pmatrix}
a_t (t)= \dfrac {dv(t)}{dt}\\
a_n (t)= \dfrac {v^2(t)}{R}
\end{pmatrix} $

et donc :

$\vec {a(t)} = \dfrac {dv(t)}{dt} \vec {u_t(t)} + \dfrac {v^{2}(t)}{R} \vec {u_n (t)}$

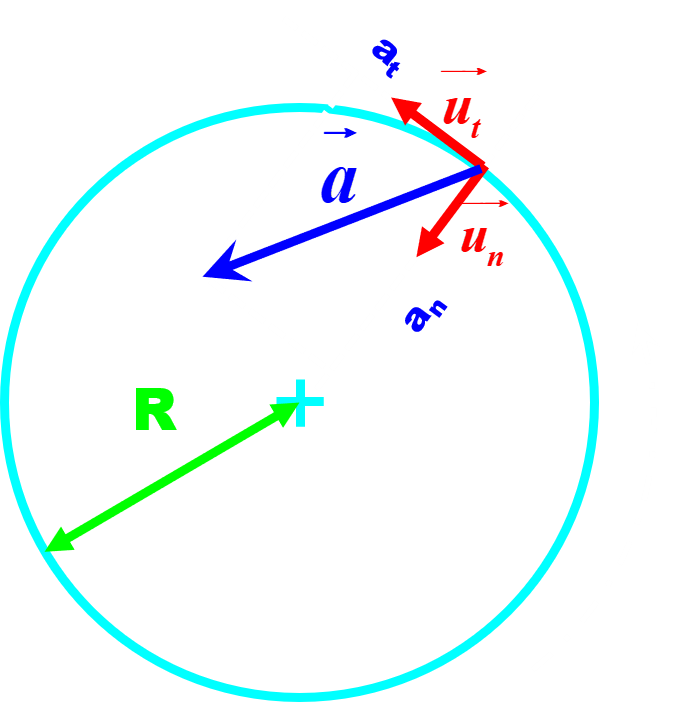C13. Mouvement circulaire uniforme.

C13a. Accélération.

Dans ce cas, la vitesse étant constante, $ \dfrac {dv(t)}{dt} = 0 $ :

l'accélération tangentielle est nulle, elle n'a pas de composante tangentielle.
La seule composante de l'accélération est sa composante normale $ \ a_n (t) = \dfrac {v^{2}(t)}{R} = \dfrac {v^{2}}{R} $ .
L'accélération est centripète.
Sa norme est : $ \ a_n (t) = \dfrac {v^{2}(t)}{R} = \dfrac {v^{2}}{R} $

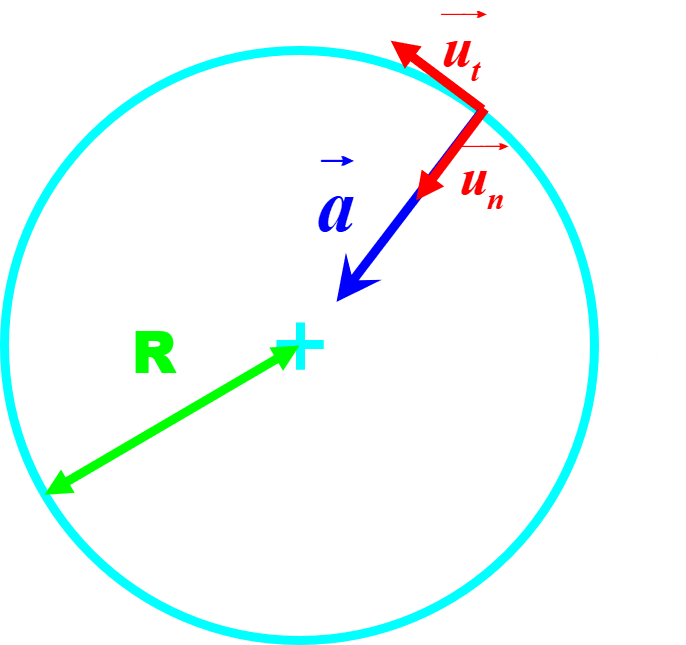C13b. Période de rotation.

Il s'agit de la durée T nécessaire au mobile pour parcourir la totalité de la trajectoire circulaire.

La longueur de la trajectoire circulaire est : $ \ L = 2 \pi R $

Le mobile parcourt donc la distance L pendant le temps T.

La valeur de sa vitesse v est alors : $ \ v = \dfrac {2 \pi R}{T}$

On en déduit celle de son accélération : $ \ a = \dfrac { 4 \pi ^{2} R }{T^{2}} $

C2. Système en orbite circulaire.

C21. Référentiel d'étude.

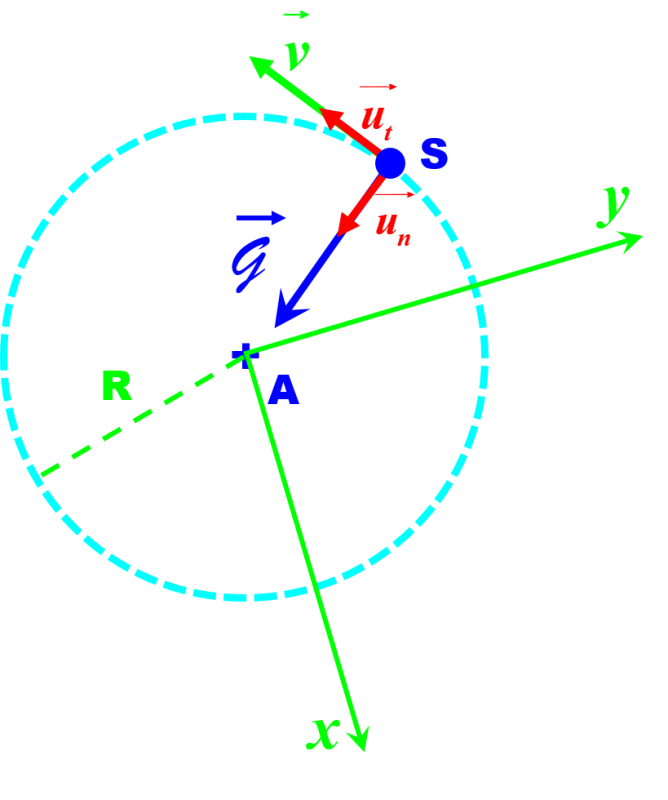
On se placera dans un référentiel astrocentrique

(A ; x ; y) lié à l'astre attracteur du satellite considéré et à des directions fixées par des étoiles très éloignées de A.

C22. Accélération.

Le satellite S et soumis à la seule force d'attraction gravitationnelle due à l'astre attracteur A dans son champ de gravitation $\overrightarrow{\cal{G}}$ :

$ \overrightarrow {{F}_ {A / B }} = G \dfrac {m_A m_S}{R^{2}} \vec {u_n}$

D'après la deuxième loi de Newton :

$ m_S . \overrightarrow {a} = G \dfrac {m_A m_S}{R^{2}} \overrightarrow {u_n}$

soit : $ \overrightarrow{a} =\vec {a_n} = G \dfrac {m_A}{R^{2}} \overrightarrow {u_n}$

NB : On retrouve le fait que du fait de l'orientation de l'accélération n'a pas de composante tangentielle, et que donc, sa vitesse est constante.

C23. Vitesse.

Du fait que : $ a = \dfrac {v^{2}}{R} : \dfrac {v^{2}}{R} = G \dfrac {m_A}{R^{2}} $ , et donc : $ v = \sqrt {\dfrac { G.m_A}{R}} $

C24. Période.

Comme on l'a montré précédemment $ \left ( a = \dfrac { 4 \pi ^{2} R }{T^{2}} \right ) $ : soit $ a = \dfrac {G.m_A}{R^{2}} = \dfrac { 4 \pi ^{2} R }{T^{2}} $

Et donc : $ \dfrac {T^{2}}{R^{3}} = \dfrac {4 \pi^{2}}{G.m_{A}} $

Remarque : Ce rapport est constant et ne dépend que de la masse de l'astre attracteur A.

On peut ainsi déterminer la valeur de la période de révolution du satellite : $ T = 2\pi \sqrt {\dfrac {R^{3}}{G.m_{A}}} $

C3. Lois de Kepler.

Johannes Kepler (1571 – 1630) formule trois lois qui décrivent le mouvement des planètes autour du Soleil en s'inspirant de ses études sur la musique.

C30 Introduction :

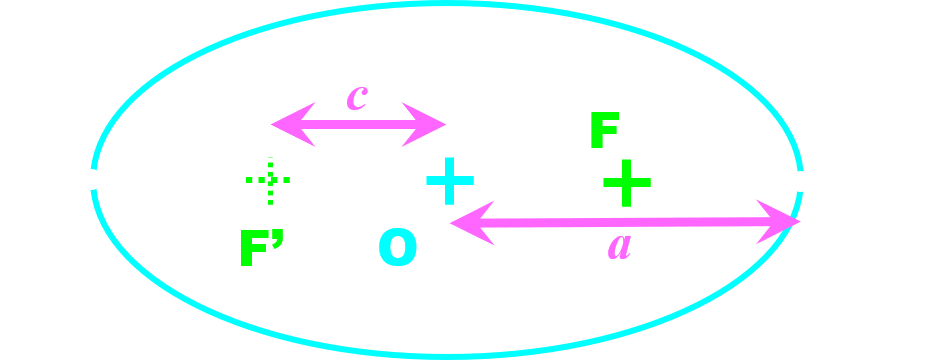
Une ellipse est une courbe caractérisée par :

- Ses foyers F et F', symétriques l'un de l'autre par rapport au point O, centre de l'ellipse.

- Quel que soit le point M de cette ellipse, on a : MF + MF' = 2a. Où a représente la longueur du demi-grand axe de l'ellipse.

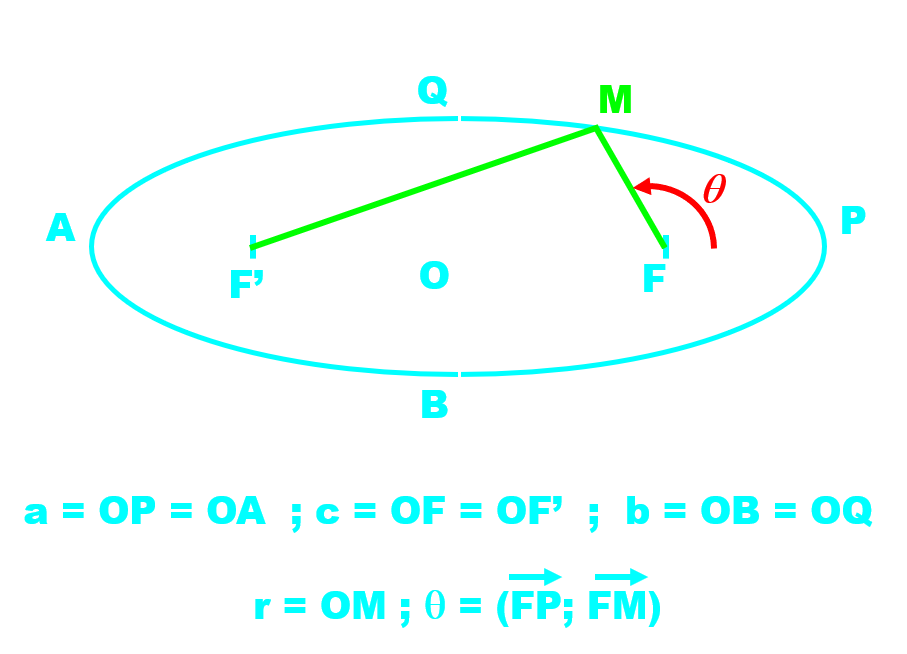
Ellipse def

Remarque : Le cercle est une ellipse particulière pour laquelle les foyers sont confondus, le demi-grand axe et le demi-petit axe on la même valeur a = b = R, rayon du cercle.

L'orbite d'une planète est la trajectoire de son centre d'inertie dans le référentiel héliocentrique.

C31. Première loi de Kepler.

Toutes les orbites de planètes sont des ellipses dont le Soleil occupe l'un des foyers.

Remarque : les planètes ne tournent pas autour du Soleil avec une vitesse constante. Quand elles se rapprochent du Soleil, leur vitesse est plus grande.

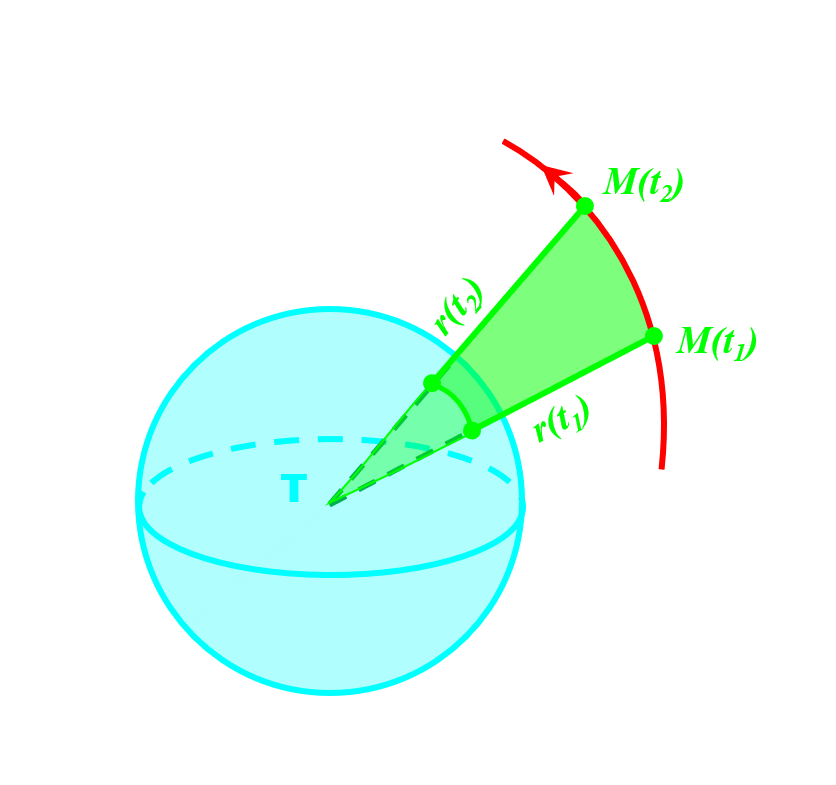
C32. Deuxième loi de Kepler

Pendant des intervalles de temps égaux Δt, le rayon balaye des surfaces S égales de l'ellipse.

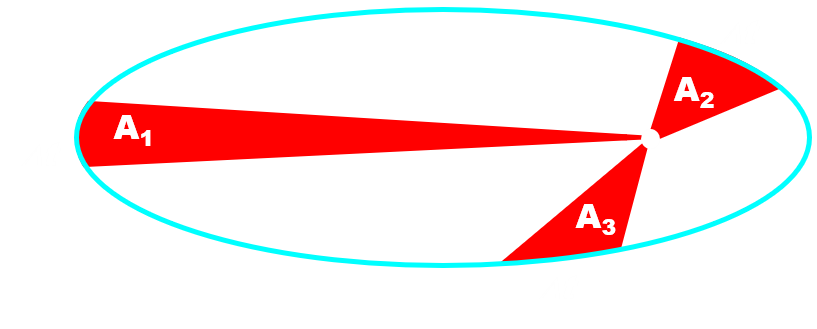
Aires