Mouvement dans un Champ Uniforme
ACTIVITES
A1 : Mouvement dans un champ de pesanteur.
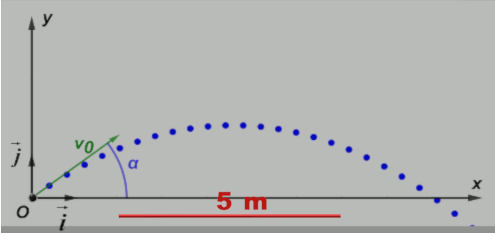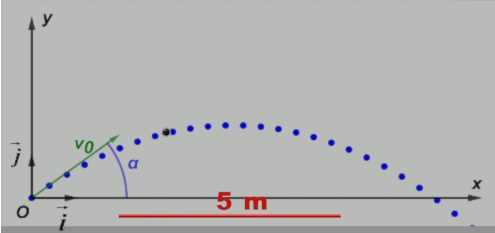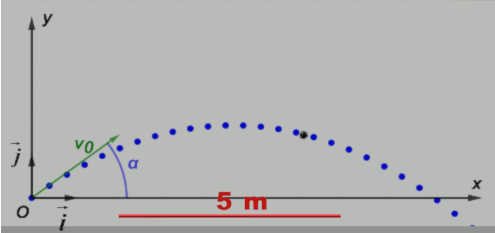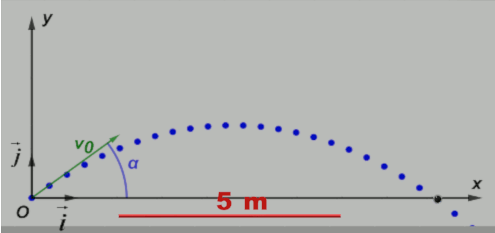
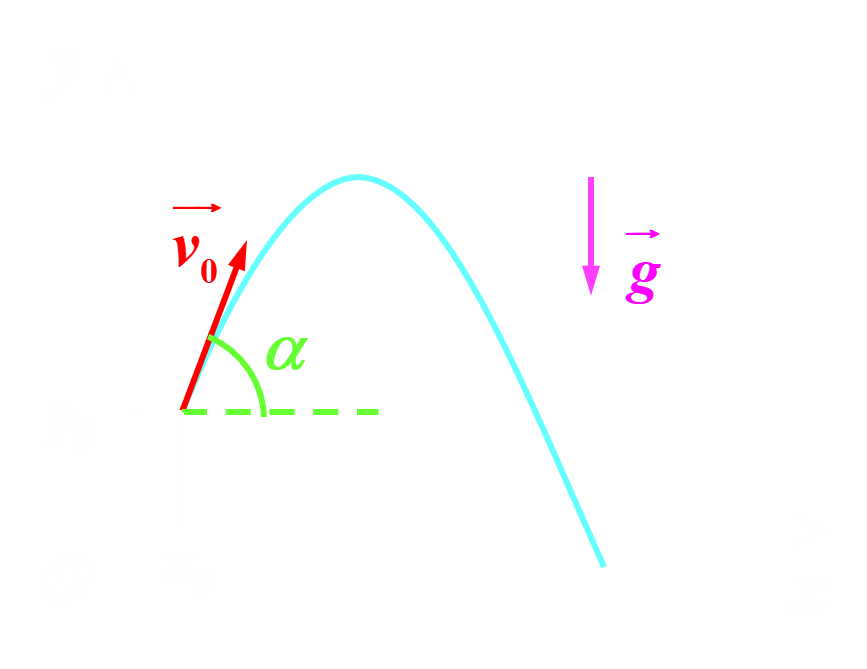
A11 : Comment établir et exploiter l'équation de la trajectoire d'un projectile dans un champ de pesanteur uniforme ?
|
|
• Comment les équations du Doc2 ont-elles été obtenues ? Appliquer de vous-même.
• Mettre en œuvre le protocole décrit dans le Doc 4. Présenter vos résultats.
• Vérifier par traitement que les coordonnées de M sont conformes à celles données dans le Doc 3.
• En utilisant l'étude précédente, déterminer les valeurs v0 et $\alpha$ de la vitesse initiale et de l'angle du lancer.
• Faire apparaître l'équation de la trajectoire y = f(x). Retrouver cette équation en utilisant le Doc5.
• Un joueur veut placer sa boule devant le cochonnet situé à 6,1 m de lui. Il lance sa boule d'une hauteur égale à 1,1 m du sol, avec un angle $\alpha = 51°$ à la vitesse v0 = 7,7 m.s-1. A-t-il réussi ?
A12. Evolution des énergies d'un système en mouvement dans un champ de pesanteur.
Quelles conversions d'énergie ont lieu lors de l'étude précédente ?
|
• A partir de l'étude précédente, ajouter les différentes formes d'énergies.
• Faire apparaître ces trois formes d'énergie sur un même graphique, exploiter ce graphique.
A2. Accélérateur de particules.
|
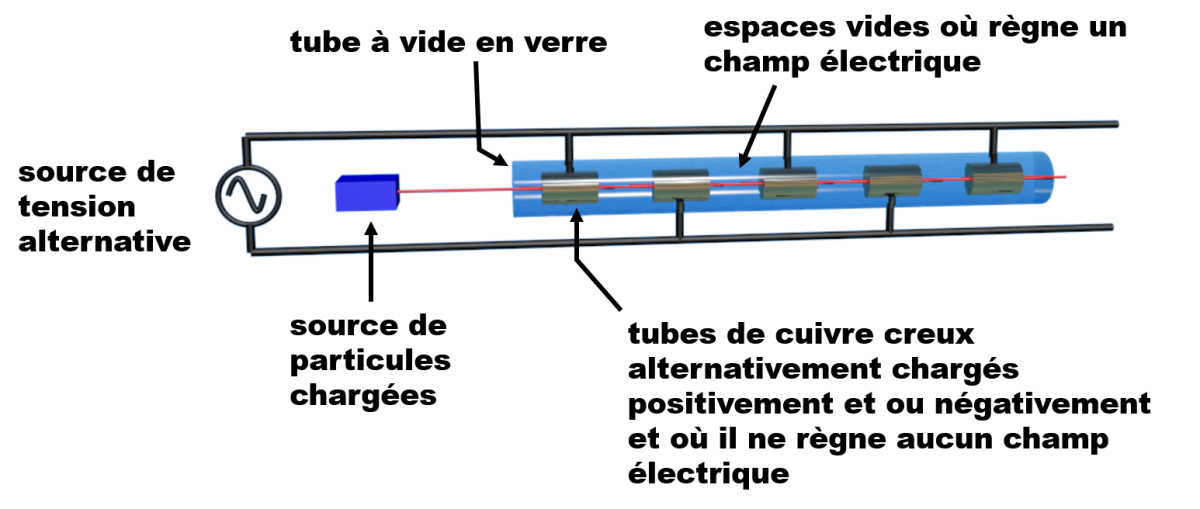
Un accélérateur de particules est constitué d'une suite de condensateurs.
Quel est le principe de fonctionnement d'un accélérateur de particules chargées ? |
 |
|
Dans un accélérateur linéaire de particules, les particules sont accélérées à chaque fois qu'elles pénètrent dans un champ électrique convenablement dirigé et orienté. La fréquence de la tension alternative appliquée entre deux tubes de cuivre consécutifs et la longueur des tubes sont calculées de sorte qu'au passage des particules, le champ électrique temporairement uniforme, soit convenablement dirigé et orienté. Les zones où règne le champ électrique peut être assimilées à des condensateurs plan. |
|
$ |
|
|
• Quelle force négligera-t-on lors de cette étude ?
• Donner l'expression de la force électrique $\overrightarrow {F_e} $ subie par le proton dans chaque condensateur.
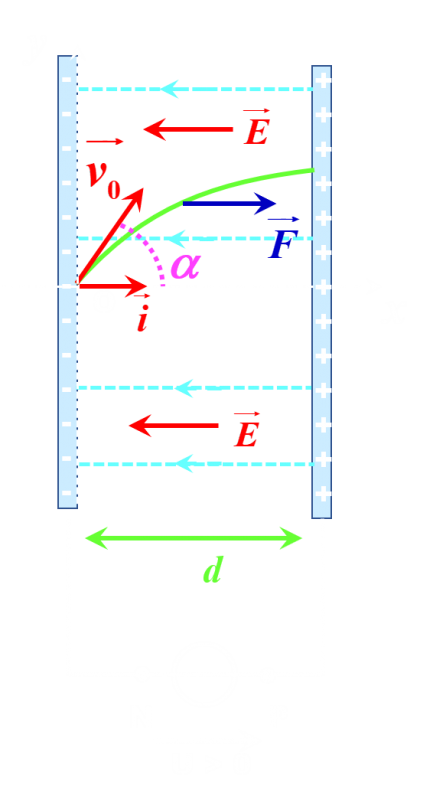
• Préciser : la charge de chaque plaque des condensateurs lorsque le proton entre dans un condensateur ainsi que la direction et le sens du champ électrique $\overrightarrow E $. Représenter la situation sur un schéma.
• Justifier alors la nécessité d'une source de tension alternative.
• Décrire le mouvement du proton ne subissant aucune force dans chaque tube.
• En utilisant le théorème de l'énergie cinétique, déterminer les longueurs L1 et L2 des deux premiers tubes. Calculer ces valeurs.
• Par un raisonnement similaire, déterminer la valeur Ln du nième tube.
A3. Imprimante à jet d'encre.
Les imprimantes à jet d'encre continu sont utilisées dans les processus industriels très rapides : marquage en série d'œufs ou de boites de conserve par exemple.
Comment contrôler la trajectoire des gouttes d'encre pour obtenir
une bonne qualité d'impression ?
|
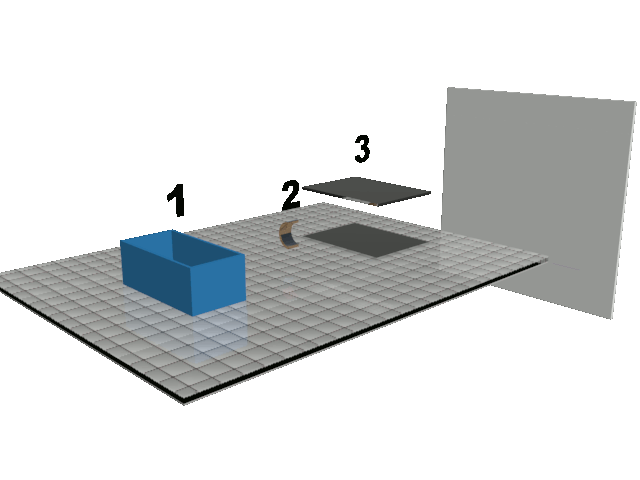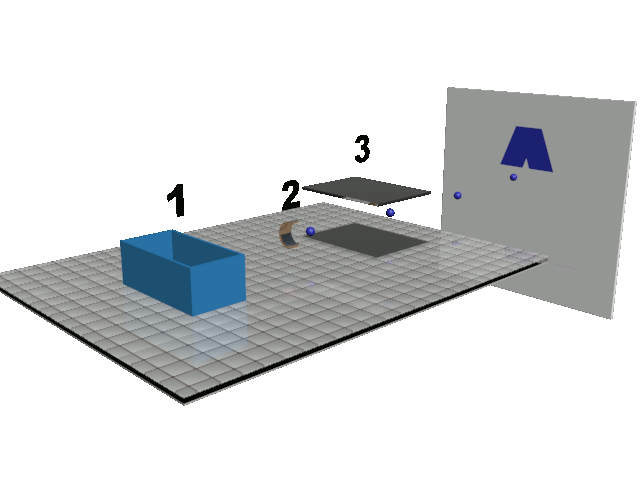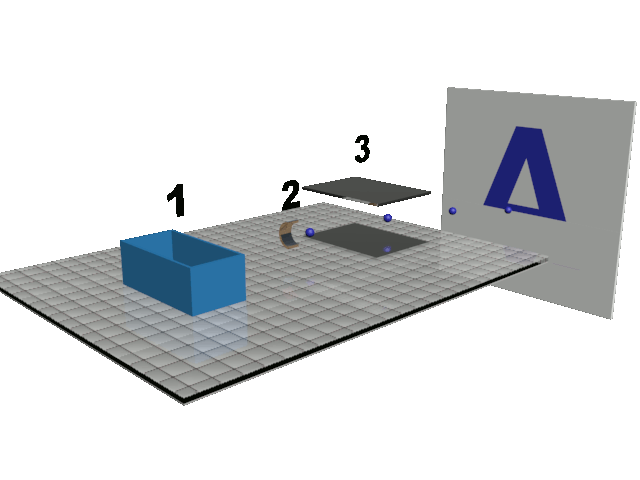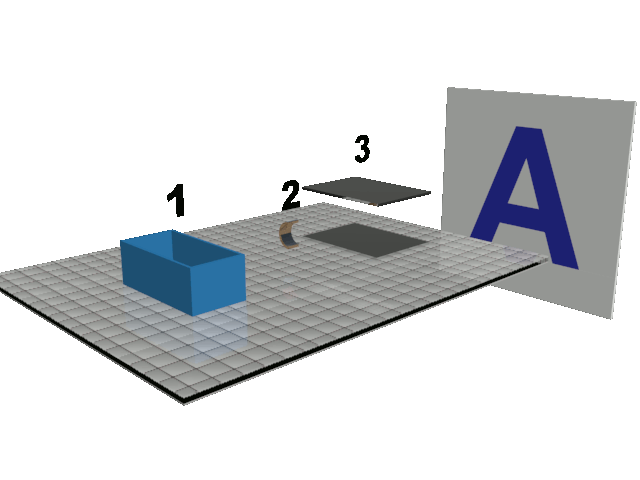
Doc1 : principe de l'imprimante à jet d'encre continu. Les gouttes d'encre pulvérisées par le réservoir 1 sont chargées au niveau de l'électrode 2, déviées à l'aide d'un champ électrique au niveau des plaques de déviation 3 puis poursuivent leur trajectoire sur le support d'impression. Les plaques peuvent être modélisées par un condensateur plan. NB : l'électrode 2 peut modifier le signe de la charge de la goutte. |
|
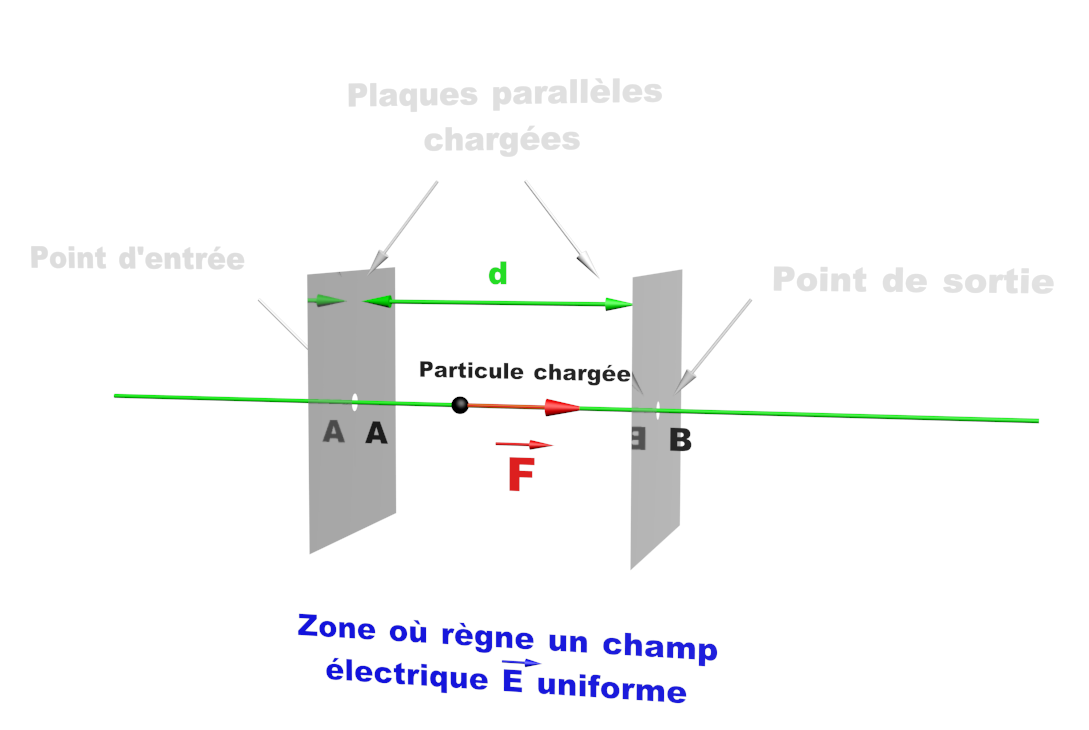
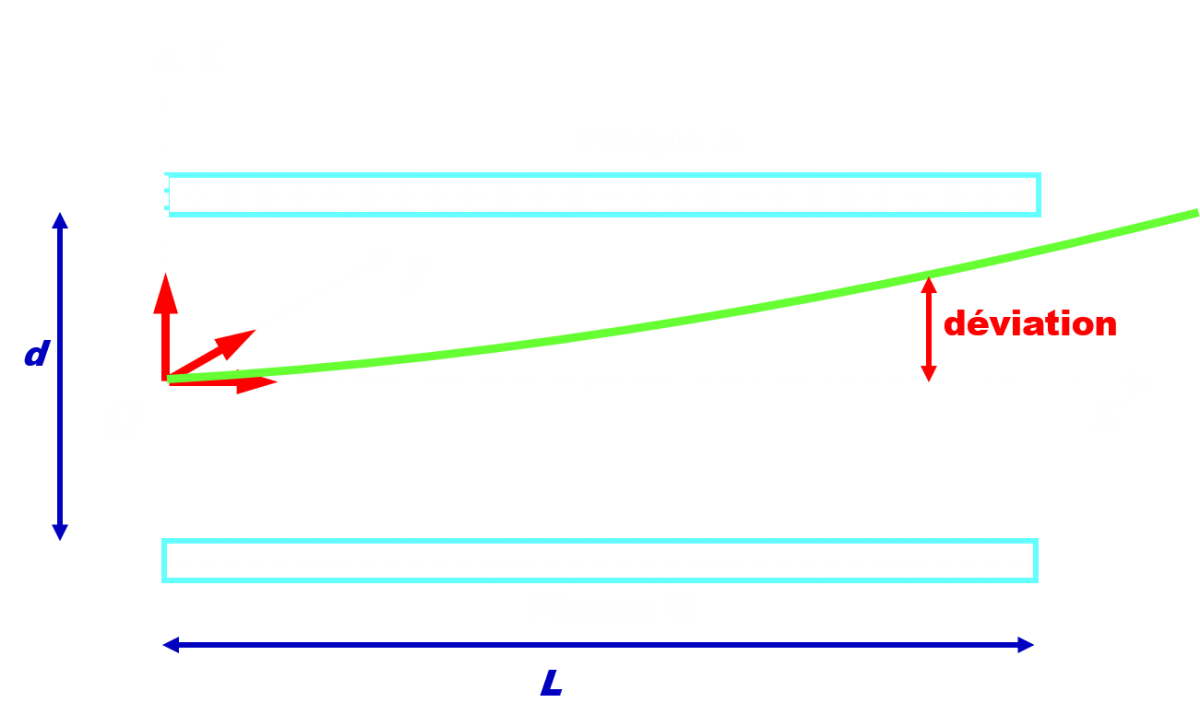
Doc2 : condensateur plan. Un condensateur plan est constitué de deux plaques métalliques chargées A et B, parallèles entre elles et séparées par un isolant. Le champ électrique uniforme $\overrightarrow E $ créé entre les plaques est relié à la distance d les séparant et à la tension électrique U appliquée entre elles : $ \overrightarrow E = - \frac {U}{d} \overrightarrow k $ |
|
Doc 3 : données. · Valeur d'éjection de la vitesse des gouttes : v0 = 20 m.s-1. · Rayon des gouttes supposées sphériques : r = 25 $\mu$m. · Masse volumique de l'encre : ρ = 9,4.102 kg.m-3. · Distance entre les deux plaques : d = 5,0 mm. · Tension électrique appliquée entre les deux plaques : jusqu'à U = 3,0 kV. · La charge des plaques peut être inversée. · Longueur des électrodes : L = 2,5 cm. |
S'approprier.
• Identifier les paramètres physiques qui influent sur le champ électrique. Et l'influence de leur déviation sur la trajectoire d'une goutte.
• Identifier l'autre paramètre qui influe sur cette déviation.
Réaliser.
• Etablir l'expression, entre les plaques A et B, du vecteur accélération $\vec a $ d'une goutte d'encre modélisée par un point matériel de masse m constante, selon sa charge q.
• A la date t0 = 0 s, une goutte d'encre pénètre dans la zone de champ uniforme au niveau du point O avec un vecteur $\overrightarrow {v_0} = v_{0} \times \vec i $ . Montrer que l'équation de la trajectoire de la goutte s'écrit : $ z = - \dfrac {qU}{2mdv^2_0} x^2 $ .
Valider, communiquer
• Présenter l'influence des différents paramètres permettant d'ajuster la déviation subie par les gouttes.
• Déterminer la charge électrique que doit posséder une goutte pour obtenir une déviation de 1 mm de déviation à la sortie du condensateur.
• Quel est sont mouvement à la sortie du condensateur ?
• Déterminer alors sa position sur le support placé à une distance D = 1m de la sortie du condensateur.
• Comment modifier le système pour que les gouttes se déplacent aussi sur l'axe des ordonnées (Oy) ?
Exercices : 9, 10 ,11,13 ,14, 15 ,18 ,20, 26 ,28, 30 ,35 P, 303 à 313
COURS
C1. Mouvement dans un champ de pesanteur uniforme.
C11. Accélération.
C11a. Rappel.
Au voisinage de la Terre, celle-ci crée un champ de pesanteur $\vec g = \dfrac {\overrightarrow P}{m} $ où $\overrightarrow P$ est le poids d'un objet de masse m.
Les caractéristiques du champ $\overrightarrow g $ ont pour caractéristiques :
• Sa direction : la verticale au lieu d'étude (du centre de gravité de l'objet vars le centre de la Terre).
• Son sens : vers la Terre
• Sa norme (considérée constante) : g = 9,81 N.kg-1.
C11b. Accélération.
D'après la deuxième loi de Newton : $\sum {\overrightarrow {F_{ext}}} = m\times \vec a $ $\overrightarrow P = m \times \overrightarrow a \Leftrightarrow m\times \overrightarrow g = m\times \overrightarrow a $
Son accélération est donc :
$ \vec a = \vec g = \begin{pmatrix}a_x(t)=0\\a_y(t)= -g\end{pmatrix}$
C12. Equations horaires du mouvement.
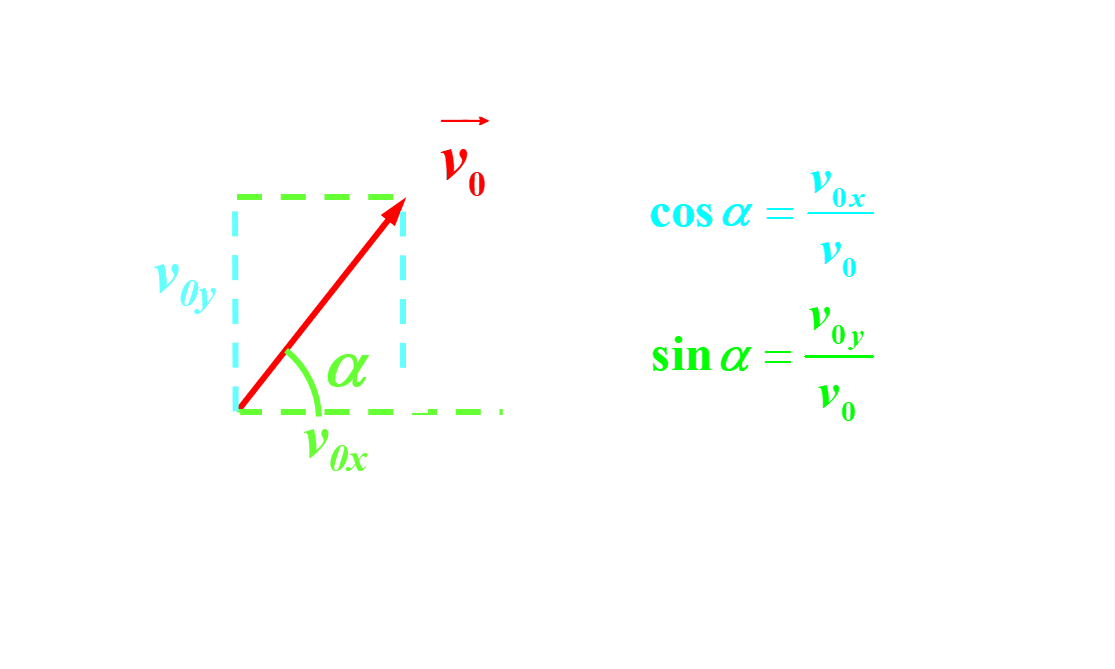
C12a. Vitesse.
Remarques :
|
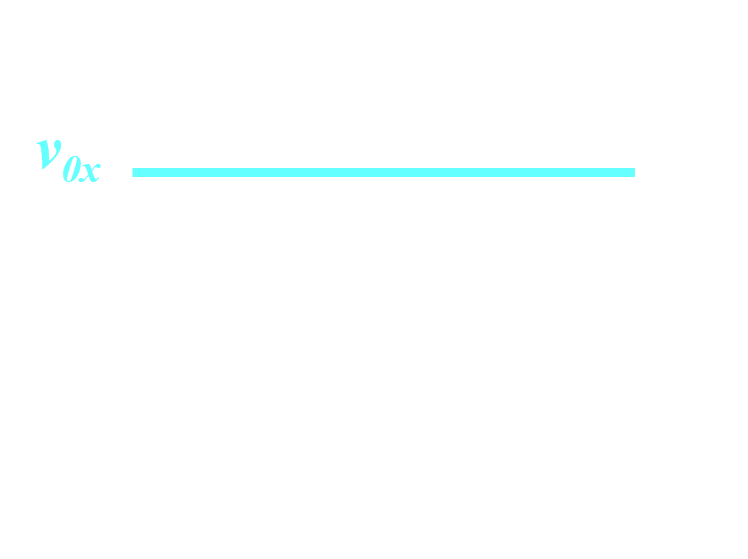
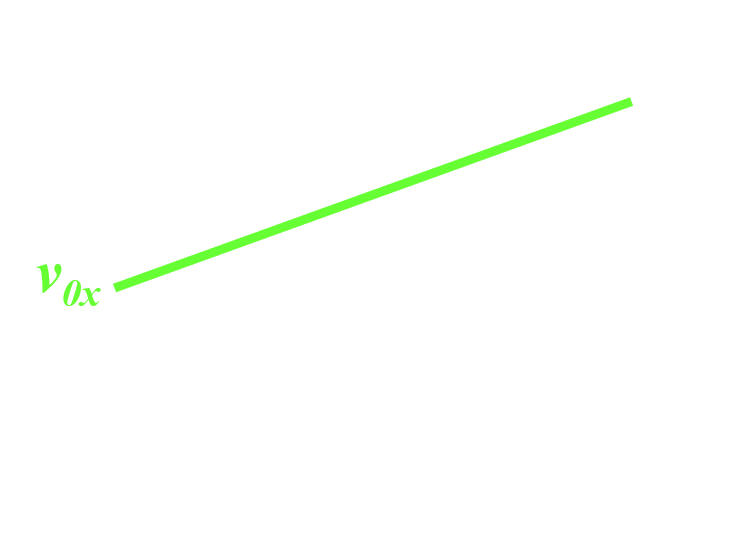
La valeur de la composante horizontale de la vitesse est constante dans le temps : |
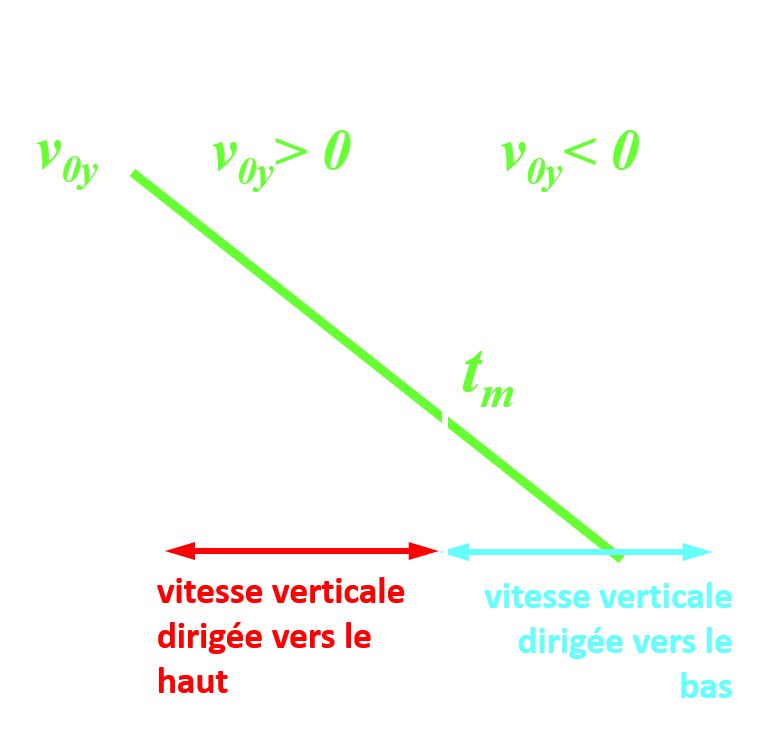
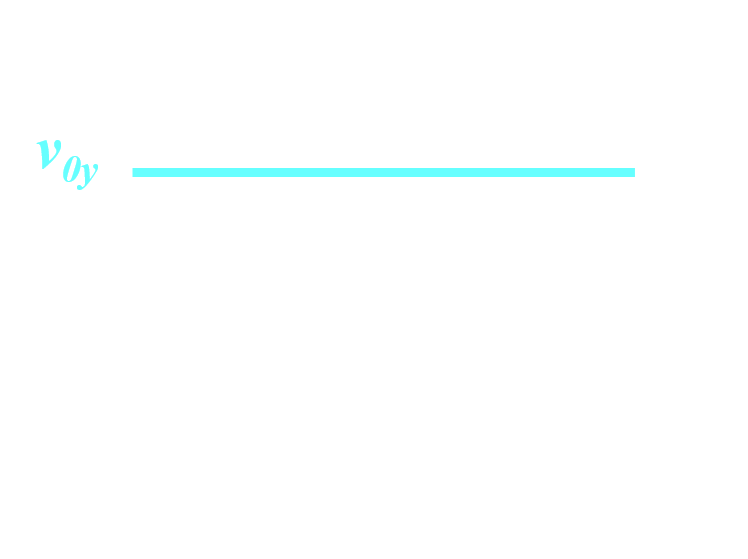
La valeur de la composante verticale de la vitesse varie linéairement en fonction du temps : Il existe un instant tm pour lequel la composante verticale de la vitesse est nulle et devient alors négative. La composante verticale de la vitesse change de sens. |
C12b. Position.
Comme $ \overrightarrow {v(t)}=\dfrac {d \overrightarrow{OG(t)}}{dt}$, on déduit de la relation précédente :
$$ \overrightarrow {OG(t)} =\begin{pmatrix} x (t) = v_0 \times cos\alpha \times t + x_0 \\
y (t) = -\dfrac{1}{2}gt^2 + v_0 \times sin\alpha \times t + y_0\end{pmatrix}$$
C13. Equation de la trajectoire.
On a obtenu ci-dessus un système d'équations paramétriques, dont le paramètre est le temps t.
En exprimant le temps en fonction de la grandeur x, on obtiendra une relation entre l'abscisse x et l'ordonnée y.
Ce qui nous donnera l'équation de la trajectoire du mobile.
Comme $ x(t) = v_0 \times cos\alpha \times t + x_0 $ : $ t = \dfrac {x-x_0}{v_0cos\alpha} $ .
En reportant dans l'équation horaire de y(t) :
$ y = - \dfrac {1}{2} g \left ( \dfrac {x-x_0}{v_0 cos \alpha }\right )^2 + v_0\times sin\alpha \times \left ( \dfrac {x-x_0}{v_0\times cos\alpha} \right )+y_0$
$ y = - \frac {1}{2} g \left ( \dfrac {x-x_0}{v_0 cos \alpha }\right )^2 + tan\alpha \times ( x-x_0)+y_0$
Il s'agit de l'équation d'une parabole ( y =Ax2 + Bx + C) où les grandeurs A, B et C constantes dépendent des conditions initiales, v0, α, x0 et y0.
C14. Aspect énergétique.
C14a. Rappels.
|
Energie cinétique : $ E_c = \dfrac {1}{2} \times m \times v^2 $ |
Energie potentielle de pesanteur : $ E_p = m \times g \times y + E_{p0} $ où Ep0 est une constante généralement prise comme nulle aux conditions initiales ou à l'altitude nulle (y = 0) |
Travail d'une force conservative :
Lors d'un déplacement de A vers B, le travail d'une force $\overrightarrow F $ s'écrit : $ W_{A \rightarrow B} \left ( \vec {F} \right ) =\overrightarrow F. \overrightarrow {AB} $
C14b. Théorème de l'énergie cinétique.
|
Dans un champ de pesanteur uniforme, la variation d'énergie cinétique entre deux points A et B est égal au travail du poids : $ \Delta E_{c \ A \rightarrow B } = E_c (B) - E_c (A) = W_{A \rightarrow B } (\overrightarrow P ) = \overrightarrow P . \overrightarrow {AB} = mg (y_B - y_A) $ |
C14c. Energie mécanique.
|
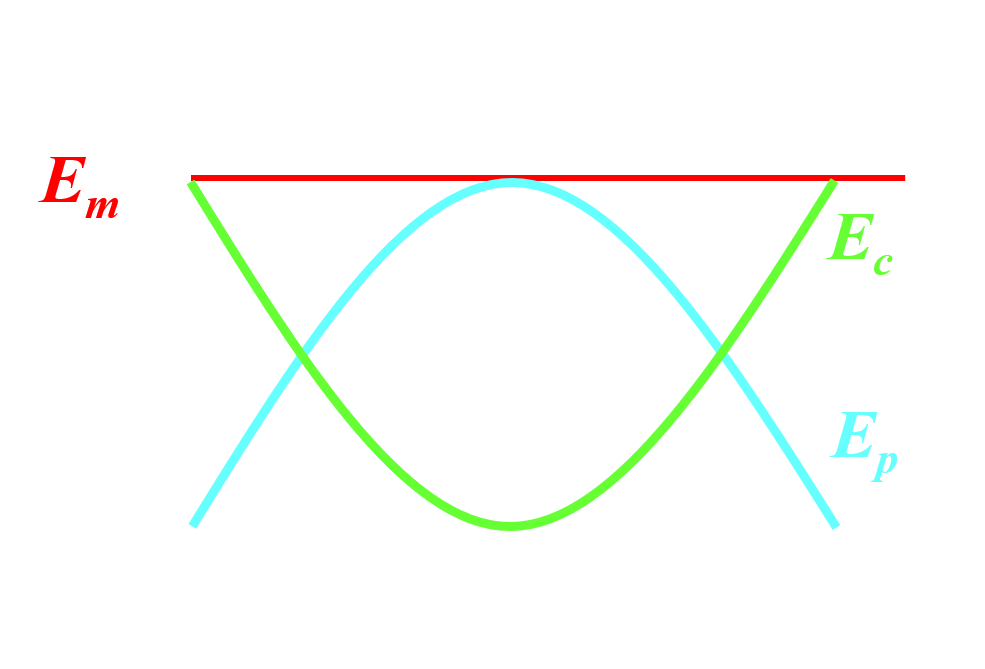 |
C2. Mouvement dans un champ électrique uniforme.
C21. Accélération.
C22. Equations horaires du mouvement.
C22a. Vitesse.
Remarques :
|
La valeur de la composante horizontale de la vitesse varie linéairement en fonction du temps : |
La valeur de la composante verticale de la vitesse est constante dans le temps :
|
C22b. Position.
Comme $ \overrightarrow {v(t)} = \dfrac {d\overrightarrow {OG(t)}}{dt} $, on déduit de la relation précédente :
$ \overrightarrow {OG(t)} = \begin{pmatrix} x (t) = \dfrac {\lvert q \rvert E}{m} \times t^2 + v_0 cos\alpha \times t\\ y (t) = v_0 sin\alpha \times t \end{pmatrix}$
C23. Equation de la trajectoire.
On a obtenu ci-dessus un système d'équations paramétriques, dont le paramètre est le temps t.
En exprimant le temps en fonction de la grandeur x, on obtiendra une relation entre l'abscisse x et l'ordonnée y.
Ce qui nous donnera l'équation de la trajectoire du mobile.
Comme $ y(t) = v_0 sin\alpha \times t $ : $ t = \dfrac {y}{v_0 sin\alpha } $ .
En reportant dans l'équation horaire de x(t) :
$ x(t) = \dfrac {\lvert q \rvert E}{2m} \left ( {\dfrac {y}{v_0sin\alpha}} \right )^2+v_0cos\alpha \times \left ( {\dfrac {y}{v_0sin\alpha}} \right ) $
$ x(t) = \dfrac {\lvert q \rvert E}{2mv^2_0 sin^2\alpha} y^2 +tan\alpha \times y $
Il s'agit de l'équation d'une parabole ( x =Ay2 + By ) où les grandeurs A, et B constantes dépendent des conditions initiales, v0, α, et aussi des valeurs de la charge q, de la masse m de la particule et de celle du champ E.
C21. Aspect énergétique.
C21. Rappels.
|
Energie cinétique : $ E_c = \dfrac {1}{2} \times m \times v^2 $
|
Energie potentielleélectrostatique : $ E_{pel} = qU + E_{p0} $ où Ep0 est une constante généralement prise comme nulle aux conditions initiales (y = 0), et U le potentiel électrosatique au point M |
Travail d'une force conservative :
Lors d'un déplacement de A vers B, le travail d'une force $\overrightarrow F $ s'écrit : $ W_{A \rightarrow B} \left ( \vec {F} \right ) = \overrightarrow {F}. \overrightarrow {AB} $
Dans la cas de la force électrostatique : $ W_{A \rightarrow B} \left ( \overrightarrow {F_{el}} \right ) = q . \overrightarrow E . \overrightarrow {AB} = qE \times d = qU $
C22. Théorème de l'énergie cinétique.
|
Dans un champ de pesanteur uniforme, la variation d'énergie cinétique entre deux points A et B est égal au travail du poids : $ \Delta E_{c \ A \rightarrow B } = E_c (B) - E_c (A) = W_{A \rightarrow B } (\overrightarrow {F_{el}} ) = qU $ |
Dans le cas où $ \overrightarrow {F_{el}}.\overrightarrow {AB} > 0 $ : la vitesse de la particule augmente.
Dans le cas où $ \overrightarrow {F_{el}}.\overrightarrow {AB} < 0 $ : la vitesse de la particule diminue.
Commentaires
-

- 1. Mamadou Bah Le 04/12/2021
Merci pour ce travail.
C'est bien préparé franchement.
Cependant, avec ces notation, j'ai du mal à très bien lire les formules.
Merci quand-même pour tout.
Ajouter un commentaire