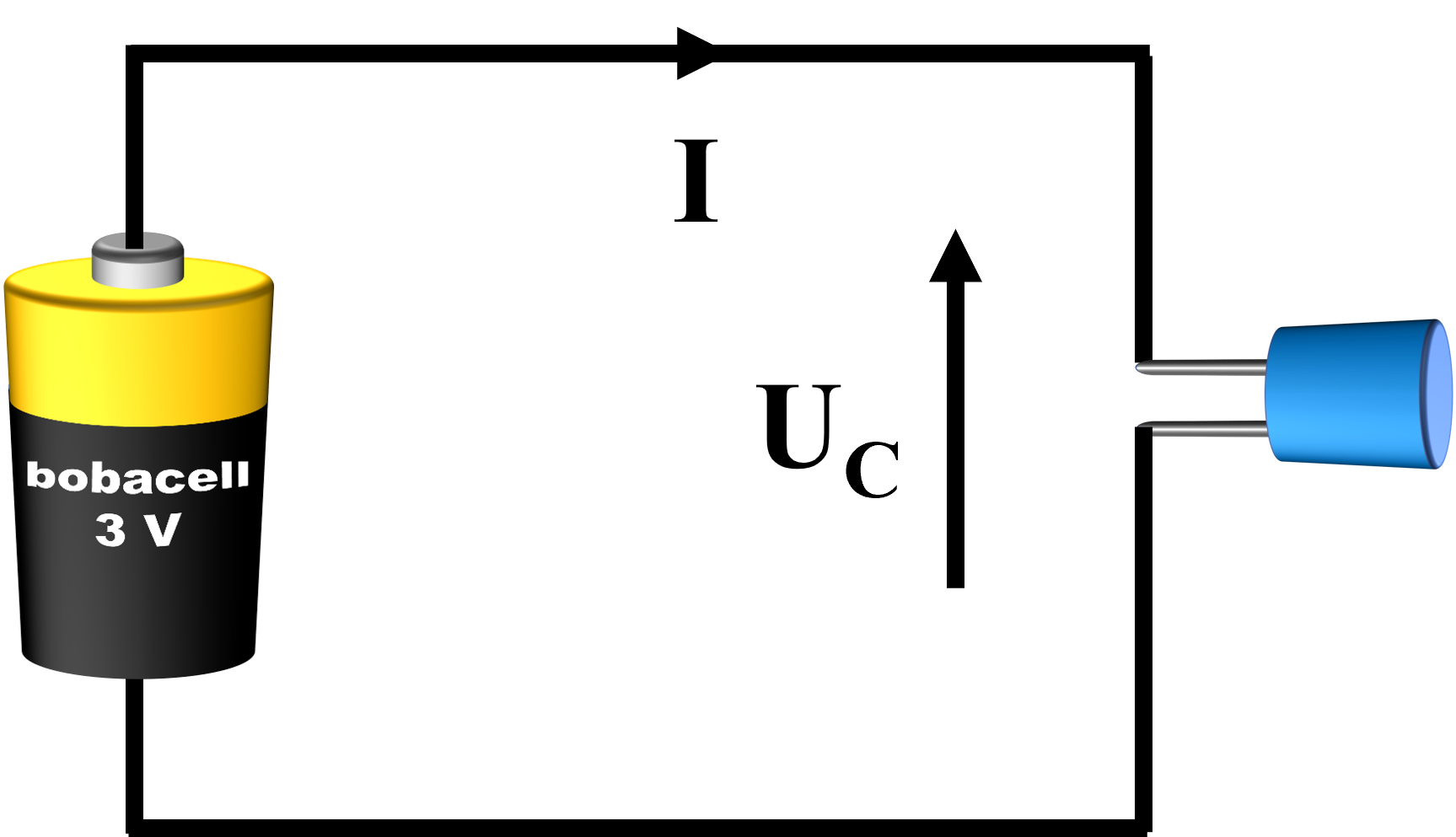Systèmes Electriques
ACTIVITES
A1. Résitor est condensateur.
En quoi le comportement d'un condensateur est-il différent de celui d'un résistor ?
A11. Présentation.
|
|
A12. Analyser.
• Expliquer la différence entre un condensateur chargé et un condensateur non chargé.
• En régime stationnaire, préciser si le condensateur se comporte comme un interrupteur fermé ou ouvert.
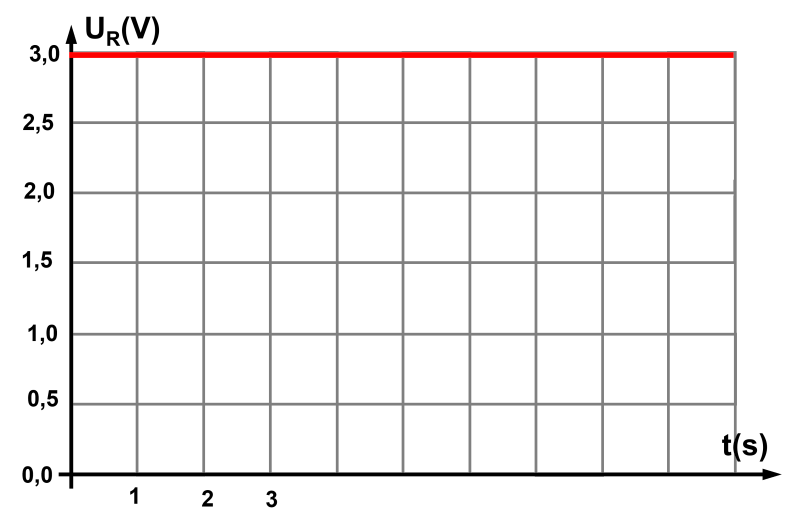
• Déterminer l'instant t pour lequel la tension aux bornes du résistor atteint sa valeur maximale.
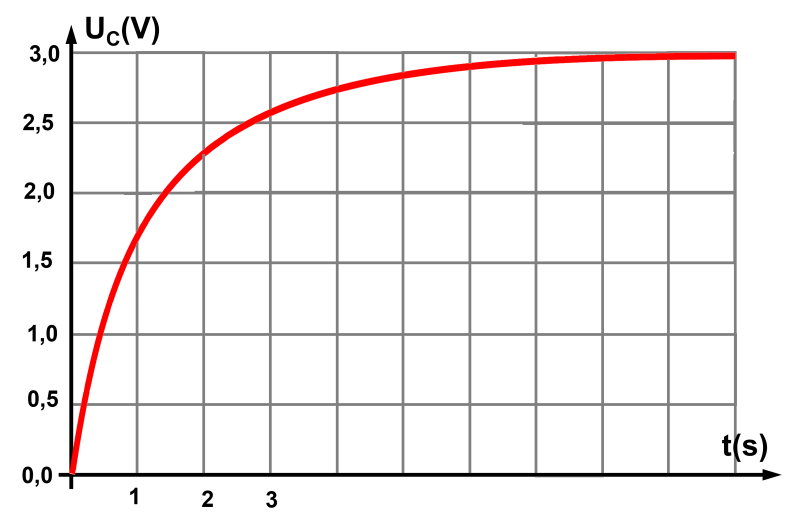
• Déterminer l'instant t pour lequel la tension aux bornes du condensateur atteint sa valeur maximale.
• En déduire la valeur du régime transitoire.
A13. Communiquer.
• Lister les principales différences entre les deux composants.
A2. Capacité d'un condensateur.
A quoi correspond la capacité d'un condensateur ?
A21. Définition.
|
Doc1 : Capacité d'un condensateur : Un condensateur initialement déchargé est branché à un générateur de courant continu d'intensité constante $I \ = \ 0,5 \ A$ La charge $Q$ est : $Q \ = \ I \times \Delta \ t$. $Q$ : charge du condensateur en coulombs (C). $I$ : intensité du courant traversant le condensateur en ampère (A). $\Delta \ t$ : durée de charge. Durant la charge, on mesure la tension aux bornes d'un condensateur soumis à une tension de 5V :
$Q$ et $u_c$ sont proportionnelles selon : $Q(t) \ = \ C \times u_c(t)$ où $C$ est la capacité du condensateur exprimée en Farad (F) |
•Déterminer la capacité du condensateur utilisé dans le Doc1.
A22. Condensateur "made in house®".
|
Doc2 : Montage. Matériel : 1 GBF 1 oscilloscope 2 feuilles de papier d'aluminium dans des pochettes. Fils électriques et pinces crocodile.
|
• Réaliser le montage ci-dessus et déterminer la valeur de la capacité C du condensateur.
A23. Caractéristiques du condensateur.
|
Doc3 : Caractéristiques d'un condensateur. · Matériau. On mesure la capacité C pour différents matériaux compris entre les armatures de même surface $S \ = \ 10 \ cm^{ \ 2}$ distantes de $e \ = \ 1,0 \ cm$.
· Distance entre les plaques pour une surface $S \ = \ 10 \ cm^{ \ 2}$.
· Pour une distance entre les armatures $e \ = \ 1 \ cm$ et un même matériau.
|
• Etudier la relation entre les caractéristiques géométriques du condensateur et sa capacité, en déterminant les relations entre $C$, $e$ et $S$. Proposer des modifications pour augmenter sa capacité.
A3. Courant électrique dans un circuit RC
Quelle est le lien entre l'intensité et la tension aux bornes d'un condensateur ? Modéliser l'évolution temporelle du système.
|
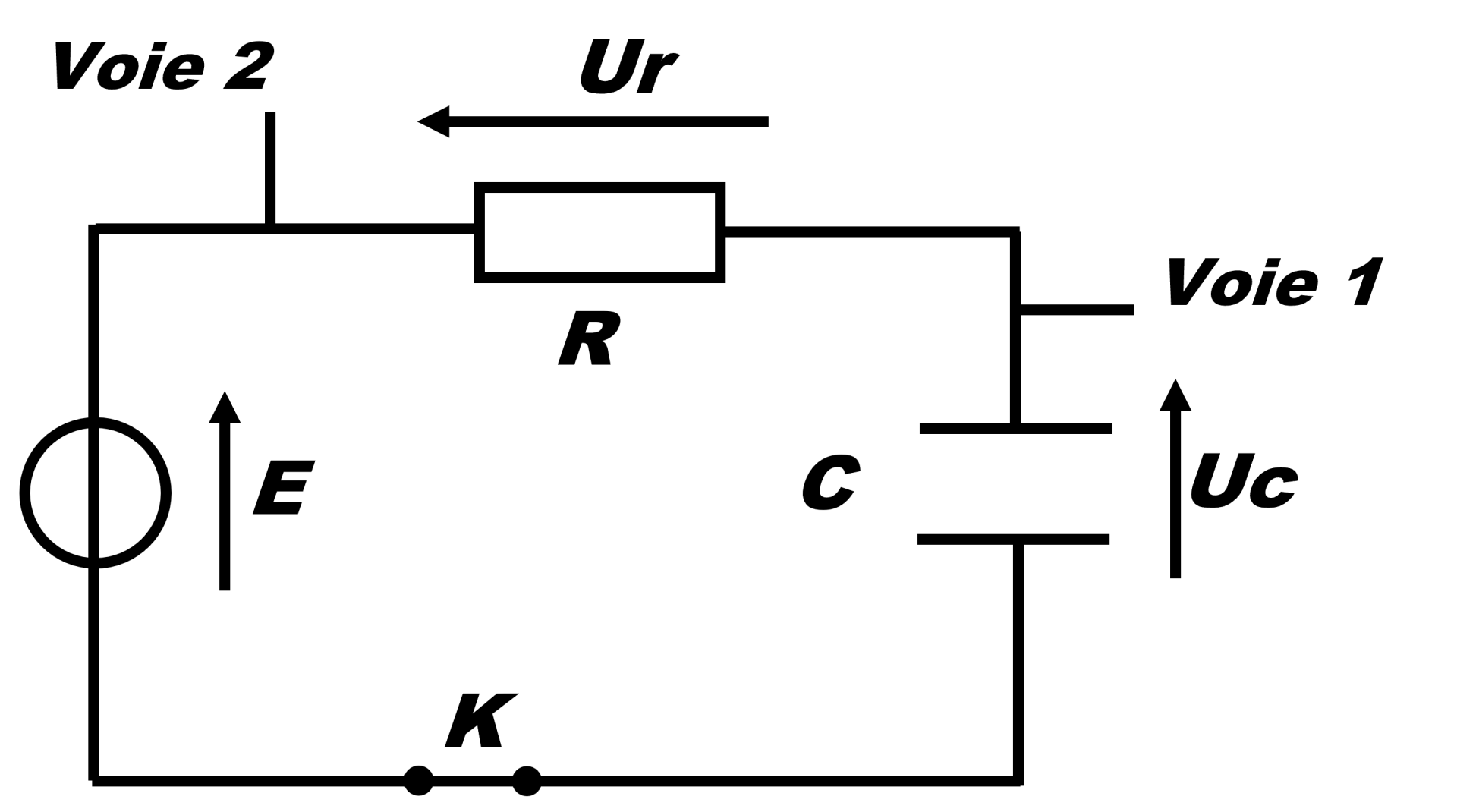
Doc1. Schéma du circuit.
|
|
Doc2 : Temps caractéristique. L'évaluation du temps $\tau \ = \ RC$ permet d'estimer le temps d'acquisition à paramétrer. Lors de la charge d'un condensateur à un temps $t \ = \ tau$, $u_C$ est égale à 63% de sa valeur finale. À $t = 5 \tau$ ce pourcentage monte à 99%.
|
|
Doc3 : Code Python. Télécharger le code ici : Cliquer ici |
A31. Réaliser.
• Réaliser le montage présenté au cours de la charge, suivre l'évolution des temps tensions $u_c(t)$ et $u_r(t)$ au cours du temps. Les représenter.
• Proposer une méthode pour obtenir l'intensité du courant $i(t)$.
• A l'aide du programme Python fourni, représenter la dérivée de la tension $u_c(t)$ par rapport au temps. Tracez alors $i(t)$ en fonction de $\dfrac{du_c(t)}{dt}$.
• Justifier que $i(t)$ est proportionnelle à $\dfrac{du_c(t)}{dt}$ . Vérifier que le coefficient de proportionnalité correspond à la capacité $C$ du condensateur utilisé.
A32. Valider.
• Déterminer la relation entre la tension uc(t) aux bornes du condensateur et l'intensité i(t) .
EXERCICES P 510 à 517
15 ; 16 ; 20 ; 22 ; 23 ; 25 ; 29 ; 35
COURS
C1. Le modèle du condensateur.
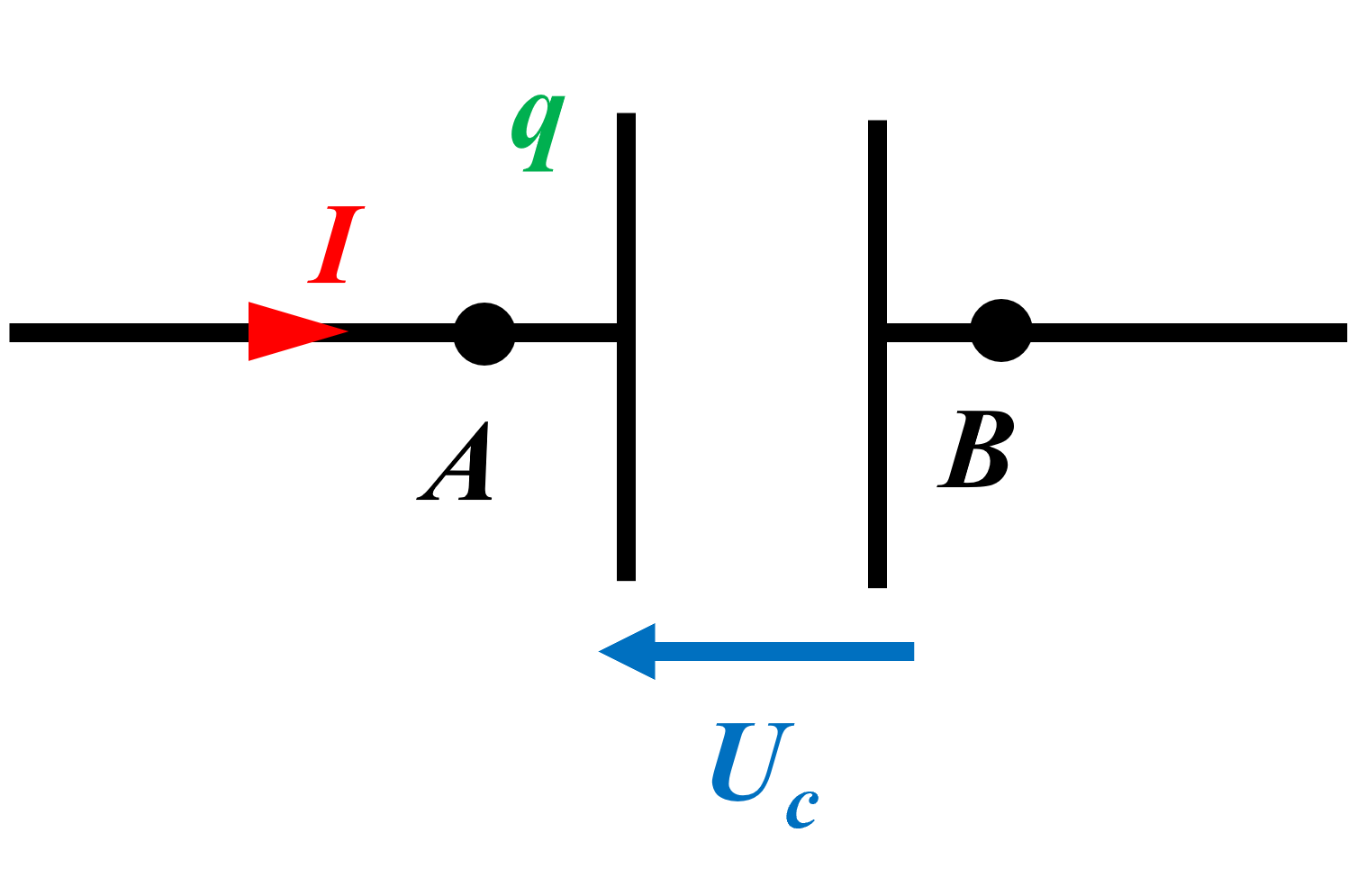
C11. Intensité du courant électrique et charge électrique.
|
C12. Le condensateur.
C12a. Principe.
En approchant un matériau conducteur chargé d'un autre matériau non chargé, il se produit une accumulation de charges opposées sur le deuxième corps (effet électrostatique).

C12b. Composant électrique.
|
C13. Capacité.
|
Définition : La charge $Q$ portée par les armatures d'un condensateur est proportionnelle à la tension $U$ entre ses armatures. Le coefficient de proportionnalité, généralement noté $C$, et appelé capacité du condensateur et dépend des propriétés du condensateur utilisé : $q \ = \ C \times U$ $q$ : charge électrique en coulomb (C) $C$ : capacité en farad (F) $U$ : tension en volt (V) |
La capacité d'un condensateur dépend de sa géométrie et du matériau isolant :
$C \ = \ \dfrac{\epsilon \times S}{e}$
$C$: capacité en farad (F)
$\epsilon$ : permittivité du constituant ($F.m^{ \ -1})$)
$S$ : surface des plaques ($m^{ \ 2}$)
$e$ : distance séparant les plaques (m)
C14. Comportement capacitif.
Des deux relations précédentes : $i(t) \ = \ \dfrac{dq(t)}{dt}$ et $q(t) \ = \ C \times U(t)$ , on en déduit que :
|
$i(t) \ = \ \dfrac{d(C \times U(t))}{dt} \ = \ C \times \dfrac{dU(t)}{dt}$ $i$ : courant électrique en ampère (A) $C$ : capacité en farad (F) $U$: tension en volt (V) |
Cette relation est une EQUATION DIFFERENTIELLE (relation entre une fonction et ses dérivées).
L'intensité $i(t)$ est en avance sur la tension $U(t)$.

C2. Modèle du circuit RC série.
C21. Charge.
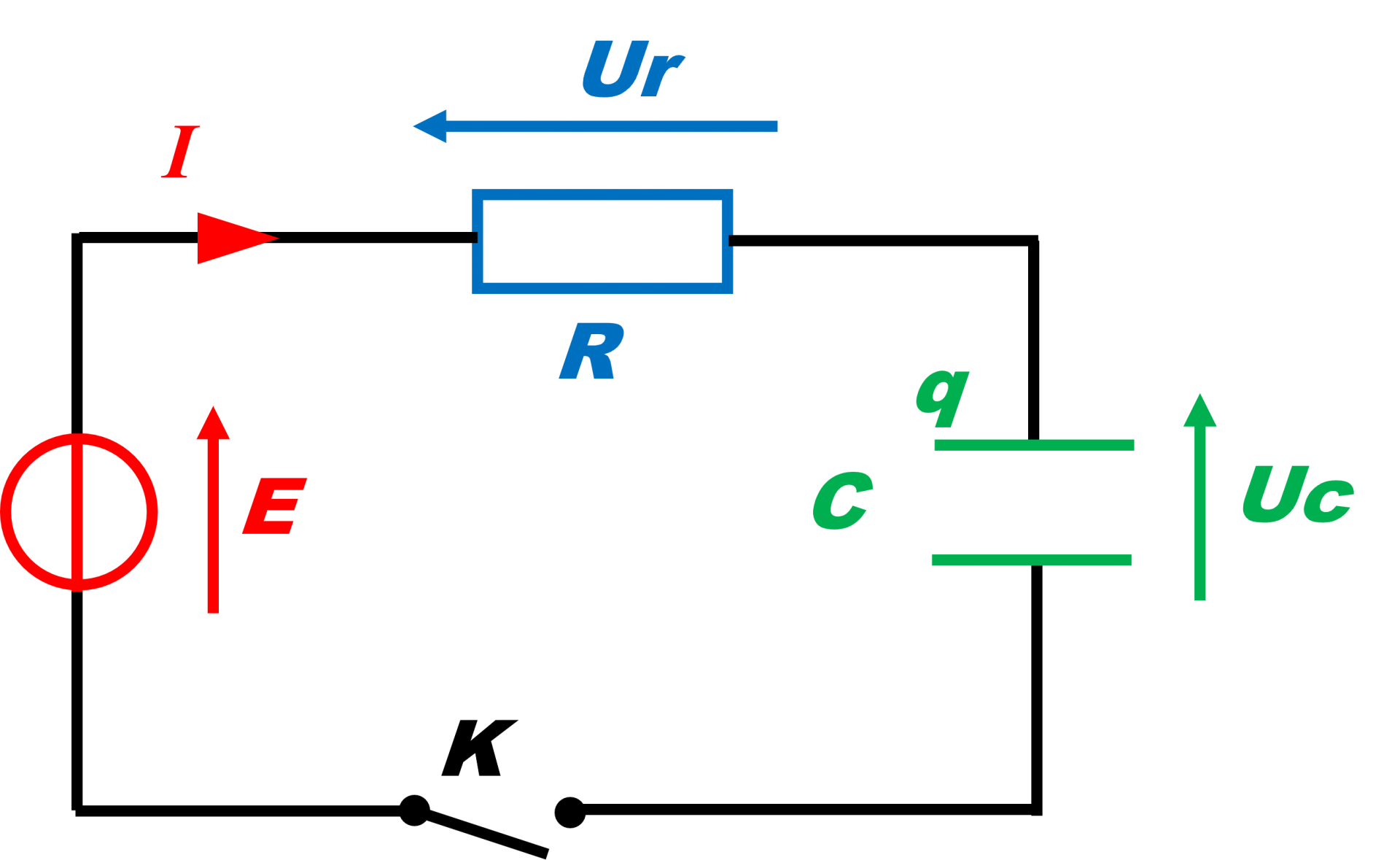 |
On considère un circuit RC. A l'instant $t = 0$, le condensateur est déchargé : $q(t = 0) \ = \ 0 \ C$. Le système est soumis à un générateur idéal de tension continue $E$. On note $U_r$ et $U_c$, les tensions respectives aux bornes du résistor et du condensateur. |
D'après la loi des mailles : $\bf{{\color{red}E} \ = \ {\color{blue}{U_r(t)}} \ + \ {\color{green}{U_c(t)}}}$
D'après la loi d'ohm : $\bf{ {\color{blue}{U_r(t) \ = \ R \ \times \ i(t)}}}$
Alors : $\bf{{\color{red}E} \ = \ {\color{blue}{R \ \times \ i(t)}} \ + \ {\color{green}{U_c(t)}}}$
On sait que : $q(t) \ = \ C \times U_c(t)$ et $i(t) \ = \ \dfrac{dq(t)}{dt}$
Donc : $E \ = \ U_c(t) \ + \ RC \times \dfrac{dU_c(t)}{dt}$
Donc : $\bf{{\color{red}{ \ \ \dfrac{dU_c(t)}{dt} \ + \ \dfrac{1}{RC} \times U_c(t) \ = \ \dfrac{E}{RC} \ \ }}} $
La relation obtenue est une équation différentielle à coefficients constants.
Les solutions sont de la forme : $\bf{U_c(t) \ = A \ \times \ e^{ \ - \ \alpha \times t} \ + \ B }$.
RESOLUTION.
• A l'instant t = 0 : le condensateur étant déchargé, la tension à ses bornes est nulle.
On en déduit : $U_c(0) \ = \ 0 \ \ \Leftrightarrow \ \ B \ = \ - \ A$.
Alors : $\bf{U_c(t) \ = A \ \times \left ( e^{ \ - \ \alpha \times t} \ - \ 1 \right ) }$
• En reportant dans l'équation différentielle :
$ A \ \times \left ( e^{ \ - \ \alpha \times t} \ - \ 1 \right ) \ - \ A.\alpha.RC.e^{ \ - \ \alpha \times t} \ = \ E$
$\Leftrightarrow \ \ A \ \times \left ( 1 \ - \ \alpha.RC \right ).e^{ \ - \ \alpha \times t} \ - \ A \ = \ E$
• Le terme E étant indépendant du temps :
|
\begin{cases} 1 \ - \alpha . RC \ = \ 0\\ et \\ A \ = \ -E \end{cases} |
$\Leftrightarrow$ |
\begin{cases} \alpha \ = \ \dfrac{1}{RC} \\ et \\ A \ = \ -E \end{cases} |
Finalement : $\bf{{\color{red}{ \ \ \ U_c(t) \ = \ E \times \left ( 1 \ - \ e^{ \ - \ \dfrac{ \ t }{RC}} \right ) }}} $
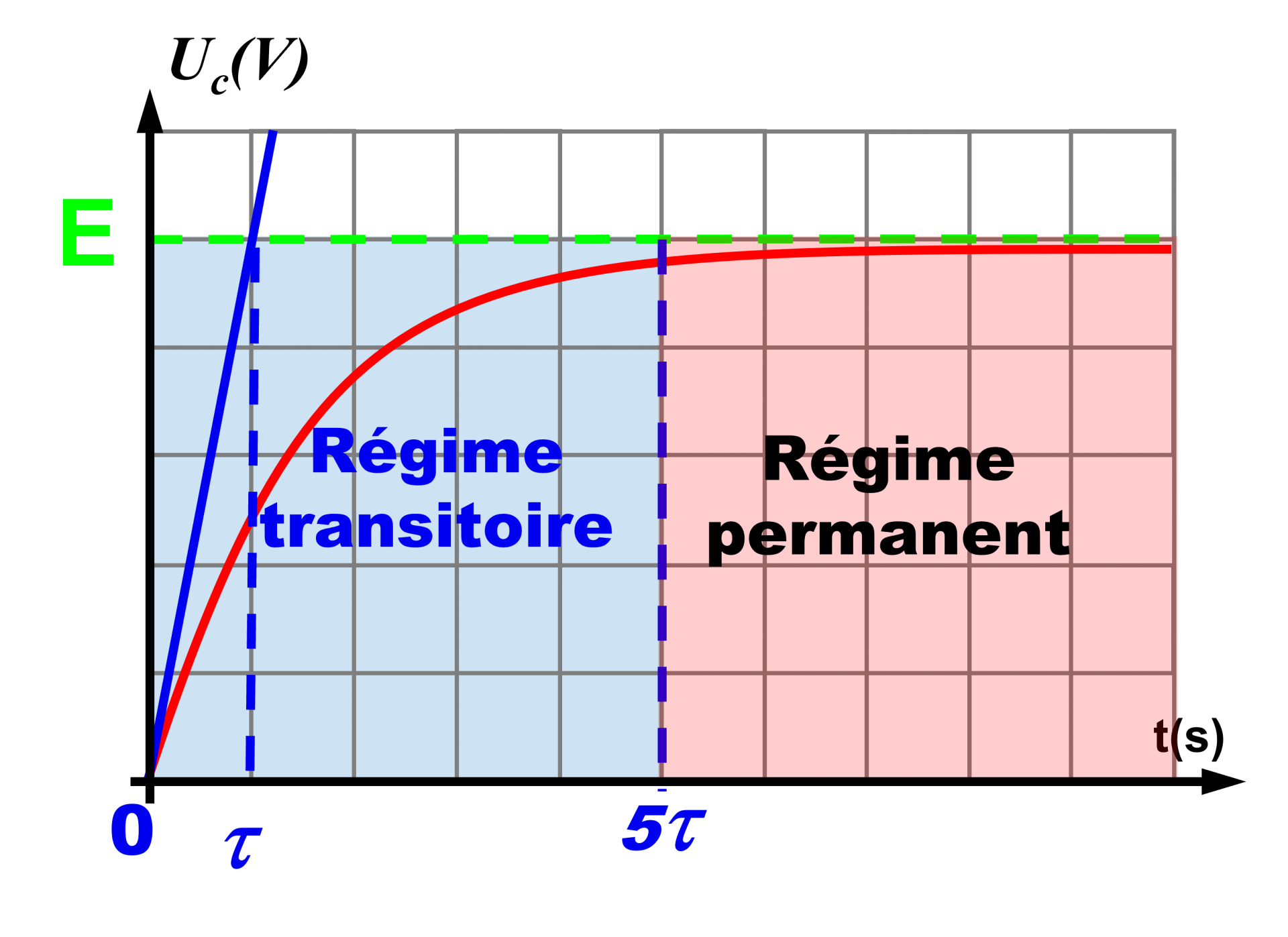 |
La tension augmente en fonction du temps jusqu'à atteindre la tension imposée par le générateur.
Dans l'intervalle où la tension varie, on parle de régime transitoire. Lorsqu'elle ne varie plus, on parle de régime permanent. |
C22. Décharge.
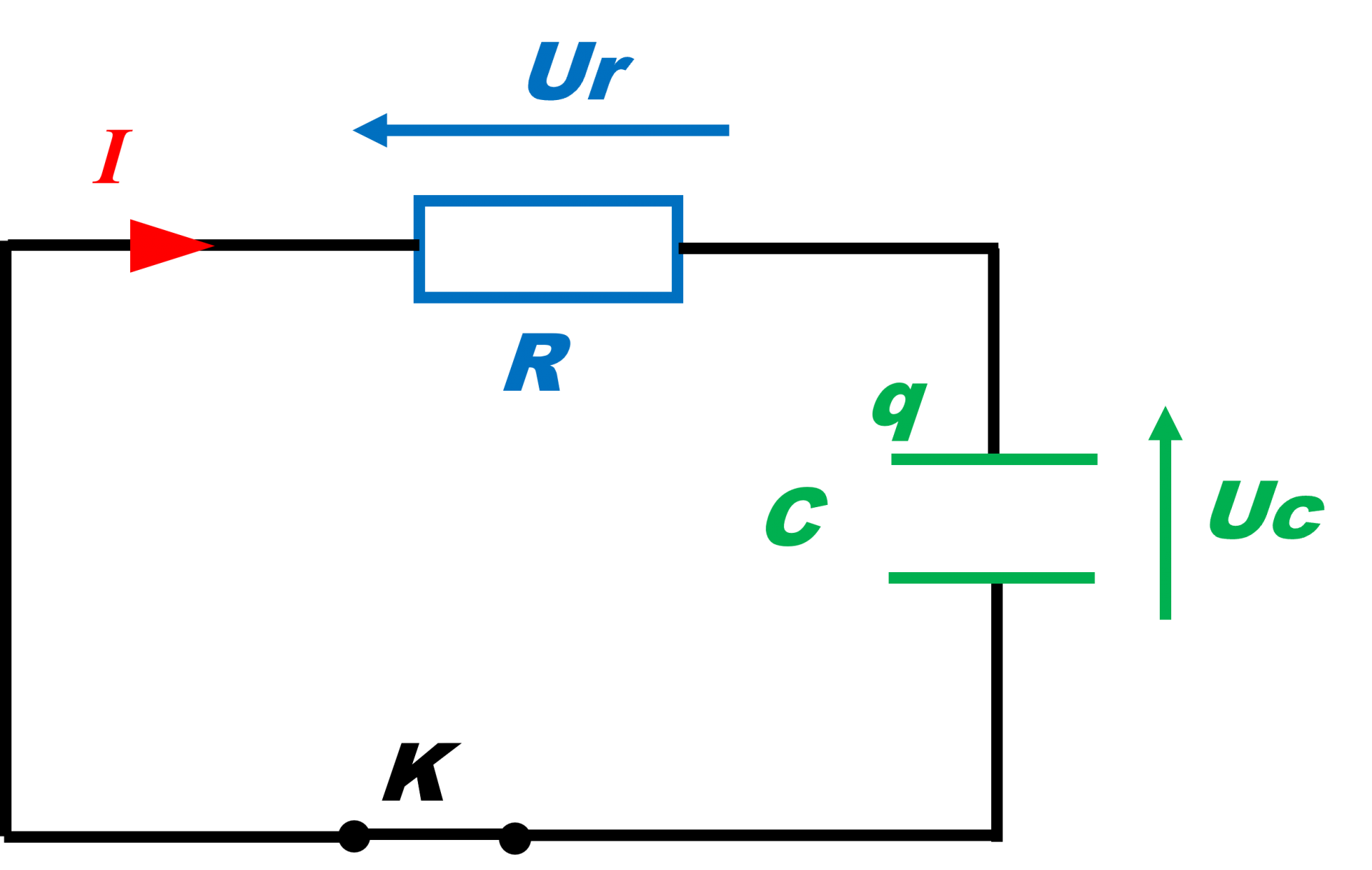 |
A l'instant $t = 0$, le condensateur chargé sous une tension E, se décharge dans le résistor.
On note Ur et Uc, les tensions respectives aux bornes du résistor et du condensateur. |
Donc : $\bf{{\color{red}{ \ \ \ U_c(t) \ + \ RC \times \ \dfrac{dU_c(t)}{dt} \ = \ 0 \ \ }}} $
La relation obtenue est une équation différentielle à coefficients constants.
Les solutions sont de la forme : $\bf{U_c(t) \ = A \ \times \ e^{ \ - \ \alpha \times t} \ + \ B }$.
RESOLUTION.
• A l'instant t = 0 : le condensateur étant chargé, la tension à ses bornes est : $U_c(0) \ = \ E \ = \ A \ + \ B$.
Alors : $\bf{U_c(t) \ = A \ \times \ e^{ \ - \ \alpha \times t} \ + \ E \ - \ A }$.
• En reportant dans l'équation différentielle :
$ A \times e^{ \ - \ \alpha \times t} \ + \ E \ - \ A \ - \ ARC \alpha \times e^{ \ - \ \alpha \times t}$.
$\Leftrightarrow \ \ A \ \times \times e^{ \ - \ \alpha \times t} \left ( 1 \ - RC \alpha \right ) \ + \ E \ - \ A \ = \ 0 $
Donc :
|
\begin{cases} 1 \ - \alpha . RC \ = \ 0\\ et \\ A \ = \ E \end{cases} |
$\Leftrightarrow$ |
\begin{cases} \alpha \ = \ \dfrac{1}{RC} \\ et \\ A \ = \ E \end{cases} |
Finalement : $\bf{{\color{red}{ \ \ \ U_c(t) \ = \ E \times \ e^{ \ - \ \dfrac{ \ t }{RC}} }}} $
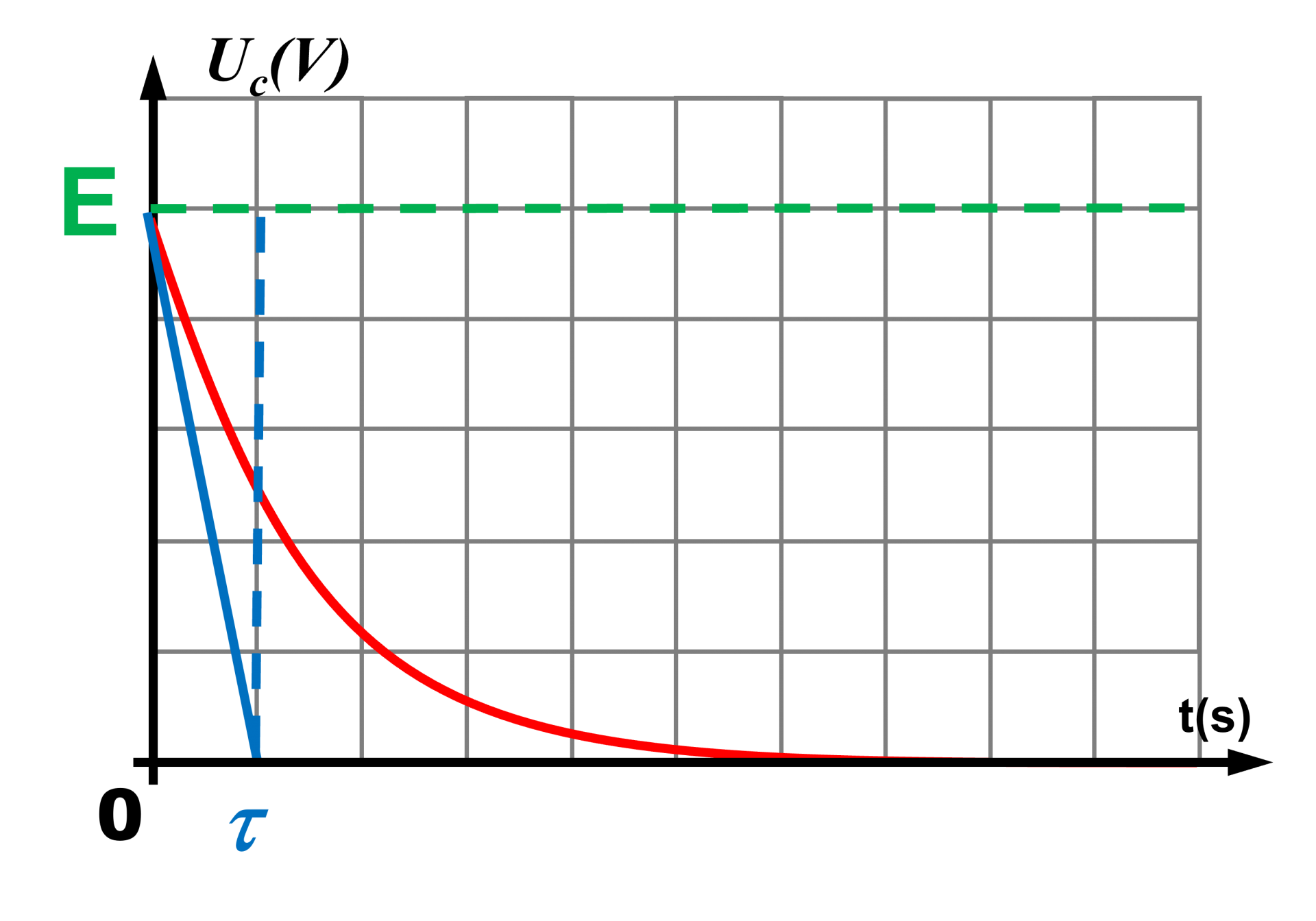 |
La tension diminue jusqu'à s'annuler. |
C23. Temps caractéristique.
C23a. Définition.
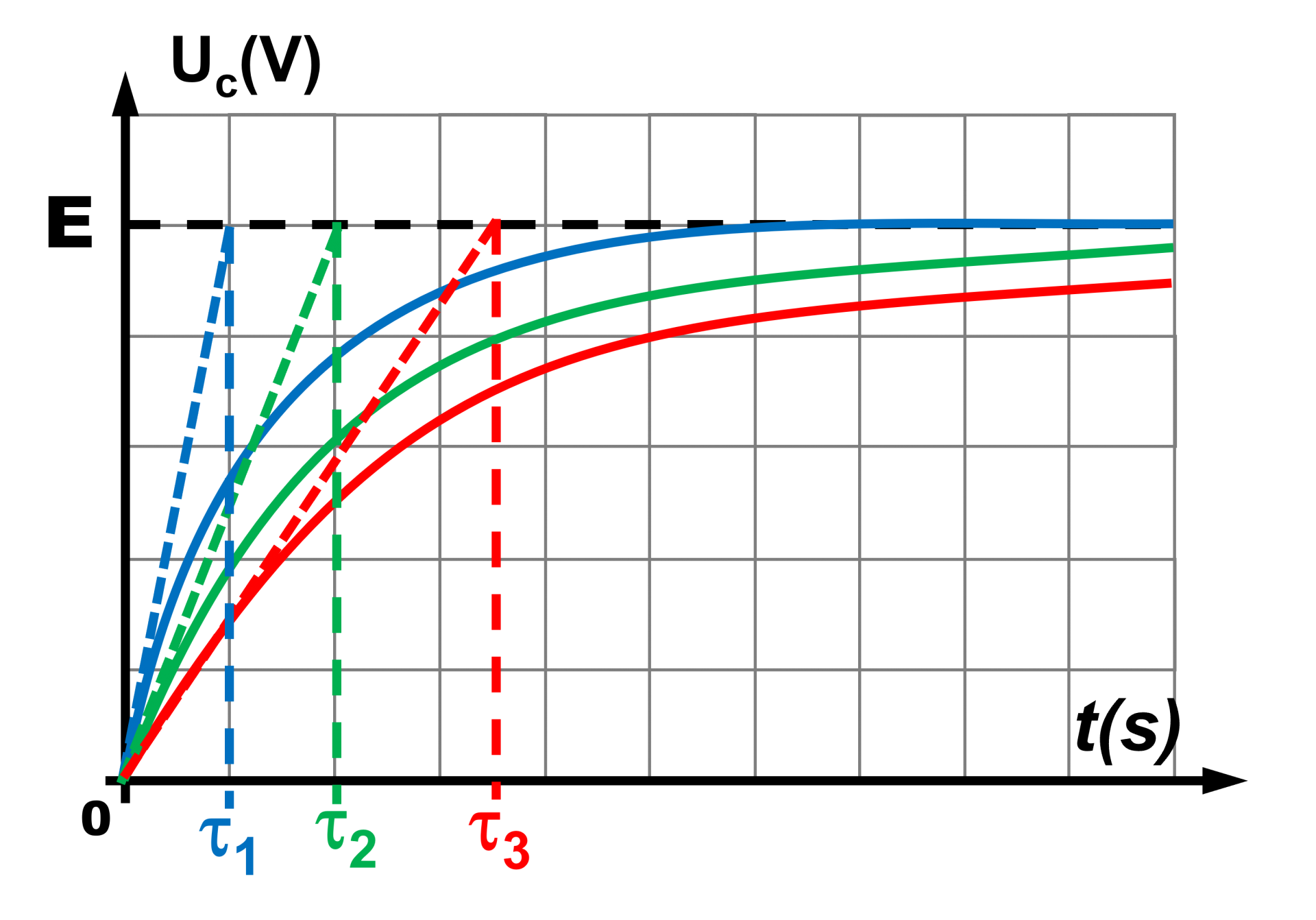
Le temps $\tau \ = \ RC$ est appelé TEMPS CARACTERISTIQUE.
Il permet d'évaluer la durée de la charge ou de décharge.
Ce temps augmente avec la valeur de R et de C.
On considère que le condensateur est chargé à $t = 5 \times \tau$.
C23b. Détermination graphique.
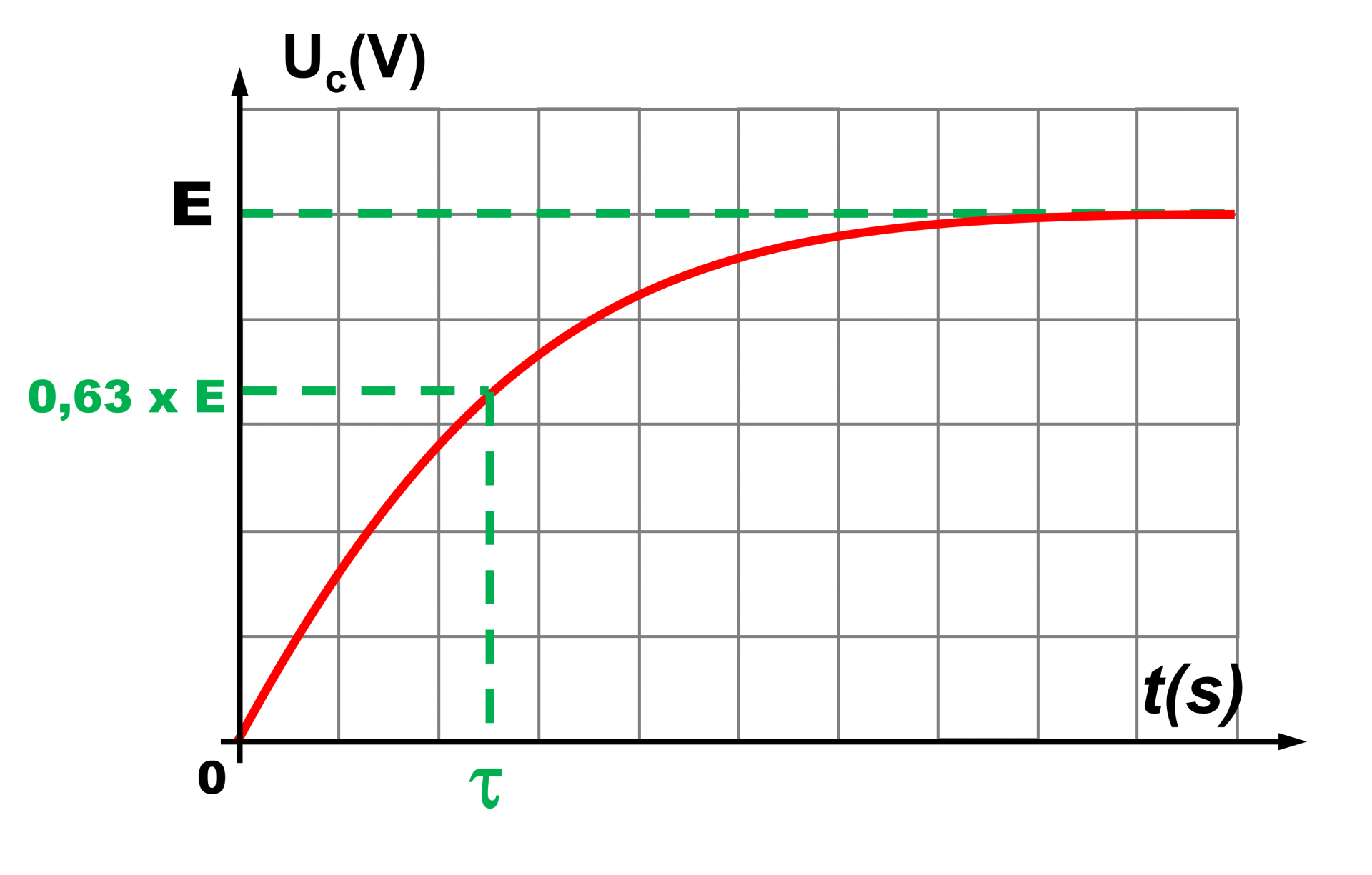
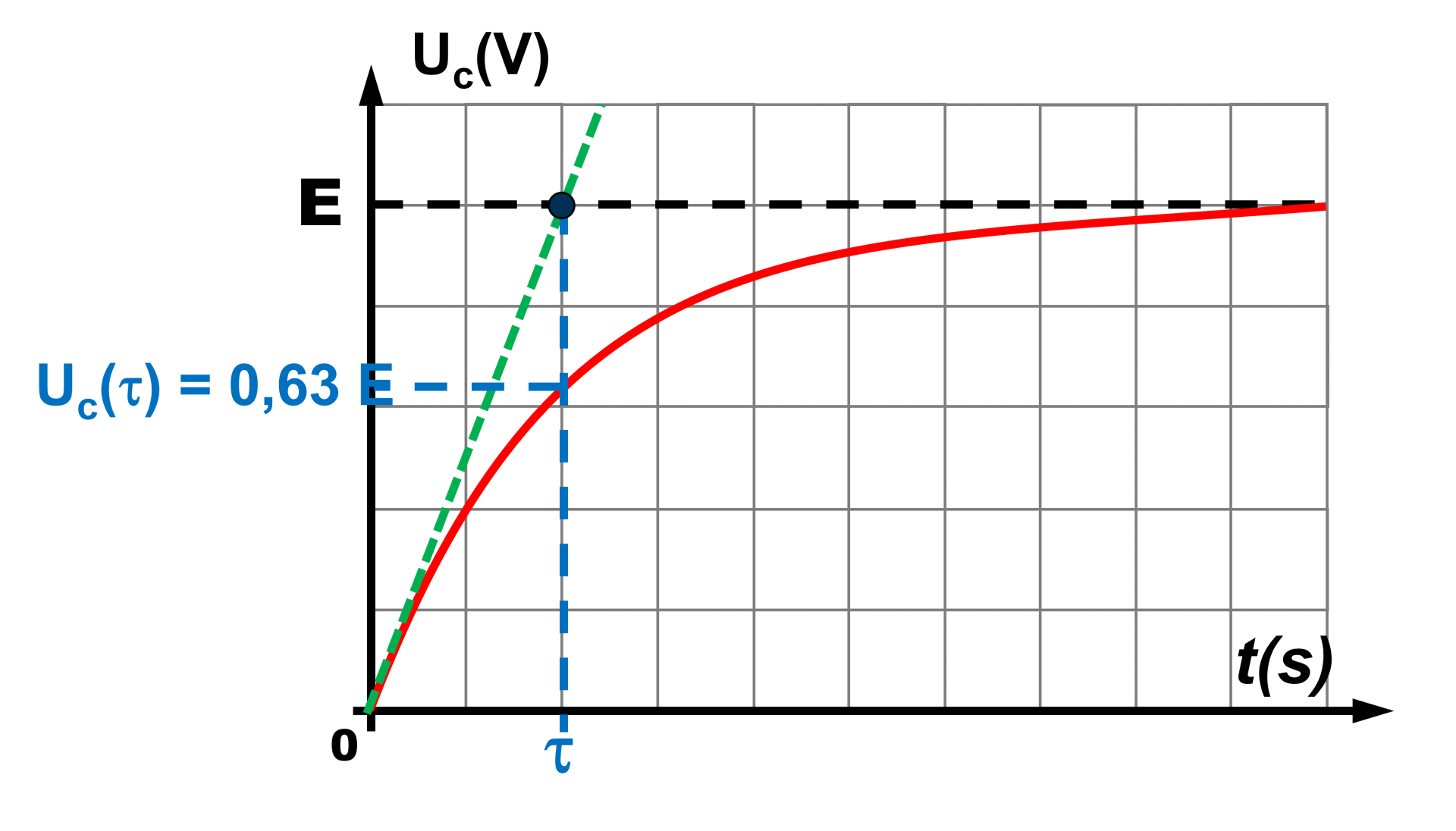
• Première méthode : on détermine $Uc(\tau)$, puis on lit graphiquement son abscisse.
• Deuxième méthode : C'est l'abscisse de l'intersection de la tangente à l'origine avec la tangente horizontale à l'infini.
NB : à $t \ = \ \tau$ : $Uc(\tau) = 0,63 \times E$.
Ajouter un commentaire