Electricité : Exercices

Exercice n°11 : Quantités de charges électriques.

1. $I \ = \ \dfrac{Q}{\Delta \ t} \Leftrightarrow \ Q \ = \ I \times \Delta \ t \ = 0,10 \times 1 \times 60 \ = \ 6,0 \ C$

2. La charge élémentaire de l'électron est : $q \ = \ \lvert -e \rvert \ = e = 1,609.10^{ \ -19} \ C$

Il faut donc : $N \ = \ \dfrac{Q}{e} \ = \ \dfrac{6}{1,602.10^{ \ -19}} \ = \ 3,7.10^{ \ 19}$ électrons, soit une quantité de matière :

Soit une quantité de matière $n \ = \ \dfrac{N}{\cal{N}_a} \ = \dfrac{Q}{e \times \cal{N}_a} \ = \ 6,2.10^{ \ -5} \ mol$

Exercice n°12 : Batterie de voiture.

1. $I \ = \ \dfrac{Q}{\Delta \ t} \Leftrightarrow \ Q \ = \ I \times \Delta \ t \ = 72 \times 1 \times 3600 \ = \ 2,6.10^{ \ 5} \ C$

2. Soit une quantité d'électrons : $N \ = \ \dfrac{Q}{e} \ = \ \dfrac{2,6.10^{ \ 5}}{e} \ = \ 1,6.10^{ \ 24}$ électrons, correspondant à une quantité de matière $n \ = \ \dfrac{Q}{e \cal{N}_a} \ = \ 2,7 \ mol$

Exercice n°13 : Décompte des charges.

1. La charge correspondante est : $Q \ = \ 1,12.10^{ \ 19} \times 1,602.10^{ \ -19} \ = \ 1,79 \ C$

2. $I \ = \ \dfrac{Q}{ \Delta \ t } \ = \ \dfrac {1,79}{3,0 \times 60} \ = 9,97.10^{ \ -3} \ A$

Exercice n°15 : Conductivité des ions.

1. L'intensité $I \ = \ \dfrac{Q}{\Delta t} \ = \dfrac{1}{\Delta \ t} \times Q$ est donc proportionnelle à la charge.

La charge totale est quant à elle proportionnelle à la quantité de charges : $Q \ = \ N \times e$. Donc : $I \ = \ \dfrac{1}{\Delta \ t} \times N \times e$

Le nombre de charges est proportionnel à la quantité de matière : $N \ = \ n \times \cal{N}_a$. Donc : $I \ = \ \dfrac{e \times \cal{N}_a}{\Delta \ t } \times n$

Comme $ n \ = \ C \times V$, $I \ = \ \dfrac{e \times \cal{N}_a \times V}{\Delta \ t } \times C$, l'intensité du courant $I$ est bien proportionnelle à la concentration $C$.

2. L'ion fer II, $Fe^{ \ 2+}$ porte 2 fois plus de charges que l'ion fluorure $F^{ \ -}$. Puisque $I$ est proportionnel à la charge, on aurait pour les ions $Fe^{ \ 2+}$ : $I_{Fe \ 2+} \ = \ \dfrac {\color{red}{2e} \times {\cal{N}}_a \times V}{\Delta \ t }$ et pour les ions fluorure : $I_{F \ -} \ = \ \dfrac {e \times {\cal{N}}_a \times V}{\Delta \ t }$

Exercice n°17 : Caractéristique d'une pile.

1. La tension à vide d'une pile est la tension mesurée à ses bornes lorsque rien n'est branché à ses bornes. L'intensité délivrée par la pile est alors de $0 \ A$.

3. L'équation de la caractéristique est une droite d'équation $U \ = \ U_0 \ - r \times I$.

Où $U_0$ représente la tenstion à vide et $r$ la résistance interne. Graphiquement, $- r$ représente le coefficient directeur de la droite.

$r= - \dfrac{9-8,7}{0-200.10^{ \ -3}} = 1,5 \Omega$ .

Exercice n°18 : A partir de la caractéristique Inensité/Tension.

1.Modélisation :

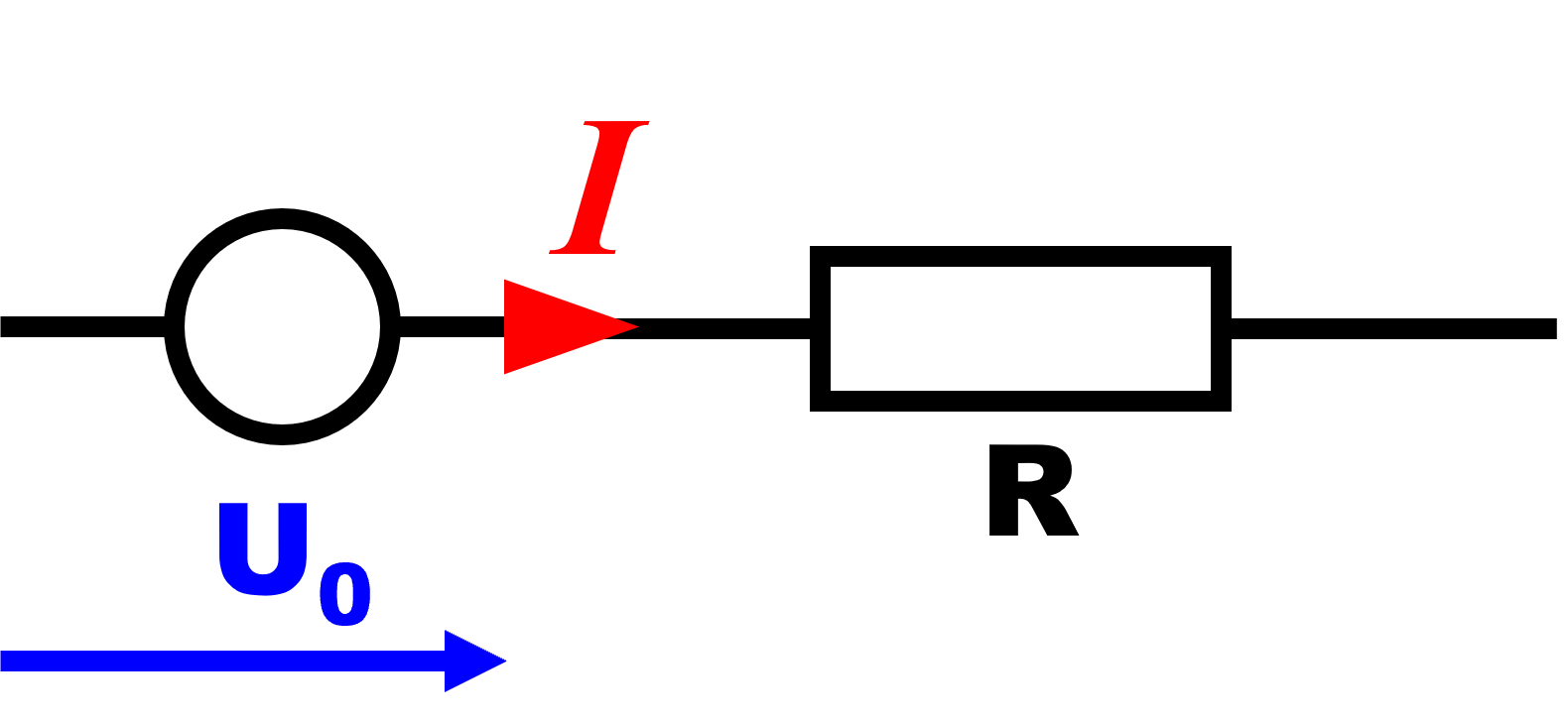
Source reelle

2.Dans le cas présent, on peut déterminer deux points particuliers :

On sait que la carectiristique Intensité/Tension est une droite d'équation : $U=U_0-r \times I$

Le coefficient directeur a pour valeur : $\dfrac{1,4-1}{20.10^{ \ -3} - 100.10^{ \ -3}} = - 5$. La résistance interne de la source de tension est donc : $r = 5 \Omega$

Au point $B \left( 100.10^{ \ -3} ; 1 \right ) : 1 \ = \ U_0 - 5 \times 100.10^{ \ -3}$ soit : $U_0 = 1+0,5 = 1,5 V$, valeur de la tension à vide.

Exercice n°20 : Qui est qui ?

1. Caractéristiques :

20 1

2, 3.

Pour le dipôle 1 : la caractéristique est une droite linéaire d'équation : $U_1 \ = \ 60 \times I$. Il s'agit d'un conducteur ohmique de résistance $R \ = \ 60 \ \Omega$.

Exercice n°23 : Entre le générateur est les lampes.

1. Rappel : Les composants du circuit sont connectés en série, l'intensité du courant traversant chaque dipôle est la même : $I \ = \ 200.10^{ \ -3} \ A$

Pour le générateur : $P_{G} \ = \ U \times I \ = \ 4,5 \times 200.10^{ \ -3} \ = \ 0,9 \ W$.

Pour la lampe $L_1$ : $P_{L_1} \ = \ 3,2 \times 200.10^{ \ -3} \ = \ 0,64 \ W$.

Pour la lampe $L_2$ : $P_{L_2} \ = \ 1,3 \times 200.10^{ \ -3} \ = \ 0,26 \ W$.

2. On constate que $P_{G} \ = \ P_{L_1} \ + \ P_{L_2}$. La puissance consommée par les lampes est bien la même que celle délivrée par le générateur.

Exercice n°26 : Energie dissipée par effet Joule.

1. $P \ = \ U \times I \ = \ R \times I^{ \ 2} \ = \ 30 \times 7,74^{ \ 2} \ = \ 1,8.10^{ \ 3 } W$

2. Ce qui correspond à une énergie : $E \ = \ P \times \Delta \ t \ = \ U \times I \ = \ R \times I^{ \ 2} \ \times 10 \times 60 = \ 1,1.10^{ \ 6} \ J$

Exercice n°27 : Le moteur électrique.

1. $E \ = \ P \times \Delta \ t \ = \ U \times I \times \Delta \ t \ = \ 10 \times 3 \times 3600 \ = 1,1.10^{ \ 5} \ J$

2. Le rendement est : $\eta \ = \ \dfrac{E_{utile}}{E_{fournie}} \ = \ \dfrac{105.10^{ \ 3}}{1,1.10^{ \ 5}} \ = \ 0,97$

3. Lénergie dissipée par effet Joule est : $E_{Joule} \ = \ 1,08.10^{ \ 5} - 1,05.10^{ \ 5 } \ = \ 3,00.10^{ \ 3} \ J$

On en déduit la puissance dissipée par effet Joule : $P \ = \ \dfrac{E_{Joule}}{\Delta \ t} \ = \dfrac {3,00.10^{ \ 3}}{3600} \ = \ 0,83 \ W$

Puis, la résistance correspondante : $R \ = \ \dfrac{P}{I^{ \ 2}} \ = \dfrac {0,83}{ 3^{ \ 2}} \ = \ 9,2.10^{ \ -2} \ \Omega \ = \ = \ 92 \ m\Omega$

Exercice n°29 : La pile à combustible.

1a. $E_{lib} \ = \ 285 \times 1,5.10^{ \ 3} \ = \ 4,25.10^{ \ 5} \ kJ \ = 428 \ MJ$

1b. L'énergie correspondante pour une heure serait : $E_{utile} \ = \ 45.10^{ \ 3} \times 3600 \ = \ 1,6.10^{ \ 8} \ = \ 162 \ MJ$

Le véhicule pourrait se déplacer pendant une durée de $\dfrac{428}{162} \ = \ 2,64 \ h \ = \ 2 \ h \ 38 \ min$

2a. La tension à vide (graphiqe) est : $U_0 \ = \ 1,48 \ V$ soit une puissance : $P_0 \ = \ U_0 \times I \ = \ 1,48 \times 2,25 \ = 3,33 \ W$

2b. Pour une intensité $I \ = \ 2,25 \ A \ = \ 2250 A$, on détermine d'après le graphique, une tension : $U \ = \ 1,445 \ V$, la puissance correspondante est : $P_{fournie} \ = \ U \times I \ = \ 3,25 \ W$

Le rendement est : $\eta \ = \ \dfrac{P_{fournie}}{P_0} \ = \ \dfrac{3,25}{3,33} \ = \ 0,98$

Exercice n°31 : Fabrication industrielle de l'aluminium.

1. C'est la présence d'ions $Al^{ \ 3+}$ et $O^{\ 2-}$ (charges libres) qui permet le passage du courant. C'est le grand nombre de cuves (360) qui sont utilisées en même temps qui permettent un grand nombre de particules libres qui permet l'intensité aussi importante.

2a. $P_{totale} \ = \ 360 \times 4,20 \times 3,5.10^{ \ 5} \ = \ 529 \ MW$

2b. $E \ = \ P \times \Delta \ t \ \Leftrightarrow \ \Delta \ t \ = \ \dfrac{E}{P} \ = \ \dfrac{4,86.10^{ \ 10}}{529.10^{ \ 6}} \ = \ 91,8 \ s$

2c. La charge totale est $Q \ = \ I \times \Delta \ t \ = 3,5.10^{ \ 5} \times 91,8 \ = \ 32 \ MC$

Exercice n°33 : Electrolyse de l'eau.

1. Les ions en solution sont des porteurs de charges (positive ou négatives), leur déplacement permet le passage du courant électrique.

2a. $E \ = \ P \times \Delta \ t \ = \ U \times I \times \Delta \ t $ donc : $I \ = \ \dfrac{E}{U \times \Delta \ t} \ = \ \dfrac{28,5.10^{ \ 3}}{1,48 \times 3600} \ = \ 5,35 \ A$

2b. La relation liant l'intensité du courant à la charge est $I \ = \ \dfrac{Q}{ \Delta \ t}$.

La charge totale nécessaire est : $Q \ = \ I \times \Delta \ t \ = \ 1,93.10^{ \ 4} \ C$

Il faut donc une quantité d'électrons : $N \ = \ \dfrac{Q}{e} \ = \ \dfrac{1,93.10^{ \ 4}}{1,602.10^{ \ -19}} \ = \ 1,20.10^{ \ 23} \ électrons$

Soit une quantité de matière en électrons : $n \ = \ \dfrac{N}{\cal N_a} \ = \ \dfrac{1,20.10^{ \ 23}}{6,02.10^{ \ 23}} \ = \ 0,20 \ mol$

3a. La solution se comportant comme un conducteur ohmique, il y aura une perte énergétique sous forme de chaleur (effet Joule).

3b. $E_{Joule} \ = \ P \times \Delta \ t \ = \ U \times I \times \Delta \ t \ = \ R \times I^{ \ 2} \times \Delta t \ = \ 1,14.10^{ \ -2} \times 5,35^{ \ 2} \times 3600 \ = \ 1,17 \ kJ$

3b. Le rendement est : $\eta \ = \ \dfrac{E_{utile}}{E_{fournie}} \ = \ \dfrac{28,5-1,17}{28,5} \ = \ 0,96 \ = \ 96 \ \%$

Exercice n°34 : La photopile.

34 1

2a.

34 1

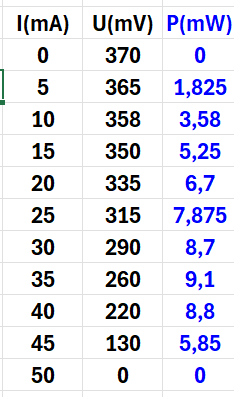
2b. Sans courant $\left( I = 0 \ A \right)$ on mesure une tension aux bornes de la photopile, et de même que pour une source de tension, lorsque l'intensité du courant dimimue, la tension diminue aussi, de même que pour une source de tension.

2c. Contrairement au générateur de tension, la fonction mathématique permettant d'exprimer U en fonction de I n'est pas une fonction simple.

3a.

34 3a

3b.

34 3b

3c,d. La puissance maximale est : $P_{max} \ = \ 9,1 \ mW$ pour une intensité $I \ = \ 35 \ mA$

Exercice n°37 : Série ou dérivation ?

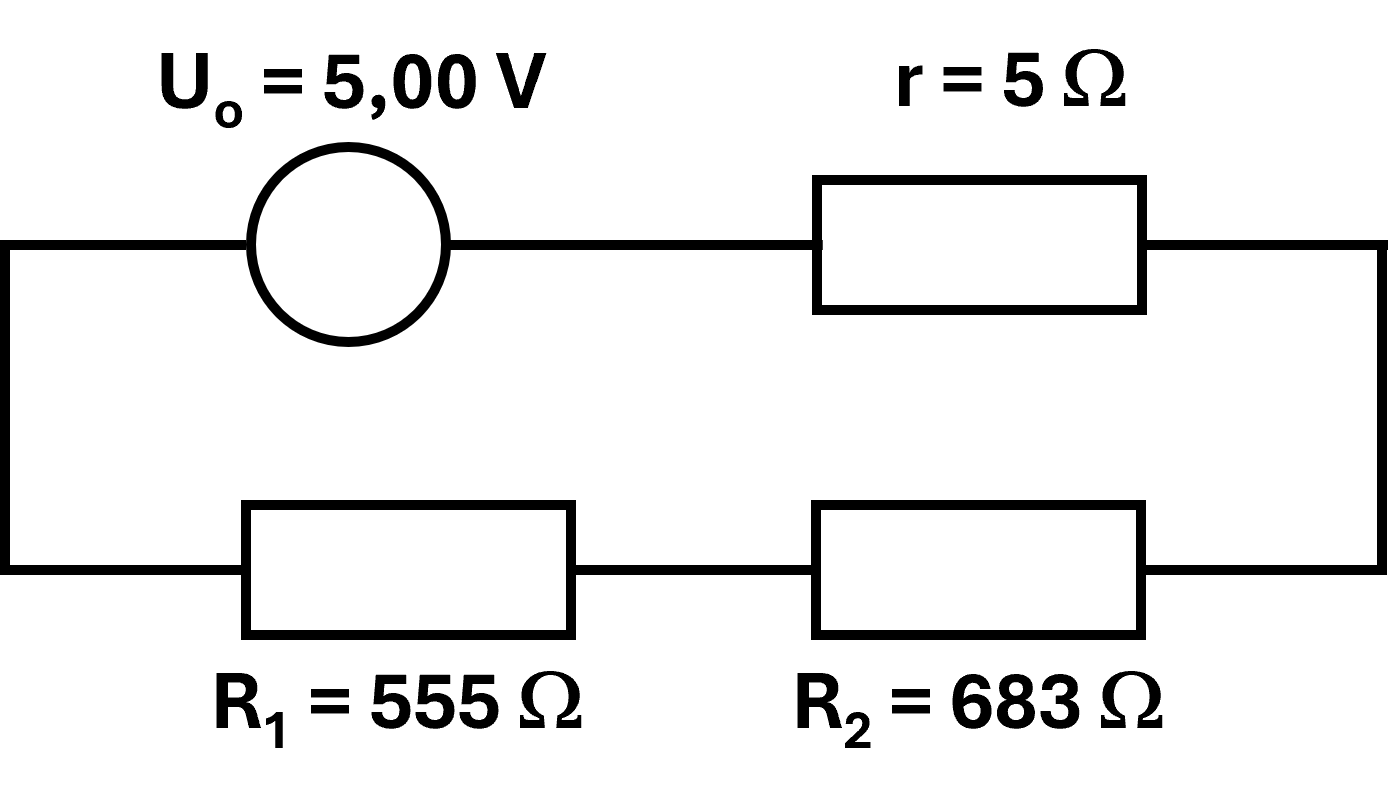
1a.

$\bullet$ La puissance délivrée par la source de tension $\left( U_0 \ ; \ r \right)$ est : $P \ = \ U_0 \ \times \ I - r \times I^{ \ 2}$

$\bullet$ La puissance dissipée par effet Joule par chaque résistor est : $P_1 \ = \ R_1 \times I^{ \ 2}$ et $P_2 \ = \ R_2 \times I^{ \ 2}$

1b. Par conservation de l'énergie (et donc de la puissance), on a :

$U_0 \ \times \ I - r \times I^{ \ 2} \ = \ R_1 \times I^{ \ 2} + \ R_2 \times I^{ \ 2}$

Soit : $I \times \left(U_0 \ - r \times I \right) = I \times \left( R_1 \times I + R_2 \times I \right)$

$\Leftrightarrow \ U_0 \ - \ r \times I \ = \ I \times \left( R_1 + R_2 \right)$

$\Leftrightarrow I \left( R_1 + R_2 + r \right) = U_0$

$\Leftrightarrow I = \dfrac{U_0}{R_1 + R_2 + r}$

1c.$I \ = \dfrac{5,00}{555+683+5} \ = \ 4,02.10^{ \ -3} \ A$

1d.Le rendement est : $\eta = \dfrac{P_{utile}}{P_{fournie}} \ = \ \dfrac{U_0 \times I - r \times I^{ \ 2}}{U_0 \times I}$

$\eta \ = \ \dfrac{U_0-r \times I}{U_0} \ = \ \dfrac{U_0- \dfrac{U_0 \times r}{R_1+R_2+r}}{U_0}$

$\eta \ = \ 1 - \dfrac{r}{R_1+R_2+r} \ = \ \dfrac{R_1+R_2+r-r}{R_1+R_2+r} \ = \ \dfrac{R_1+R_2}{R_1+R_2+r} \ = \ \dfrac{555+683}{555+683+5} \ = 99,6 \%$

37 2

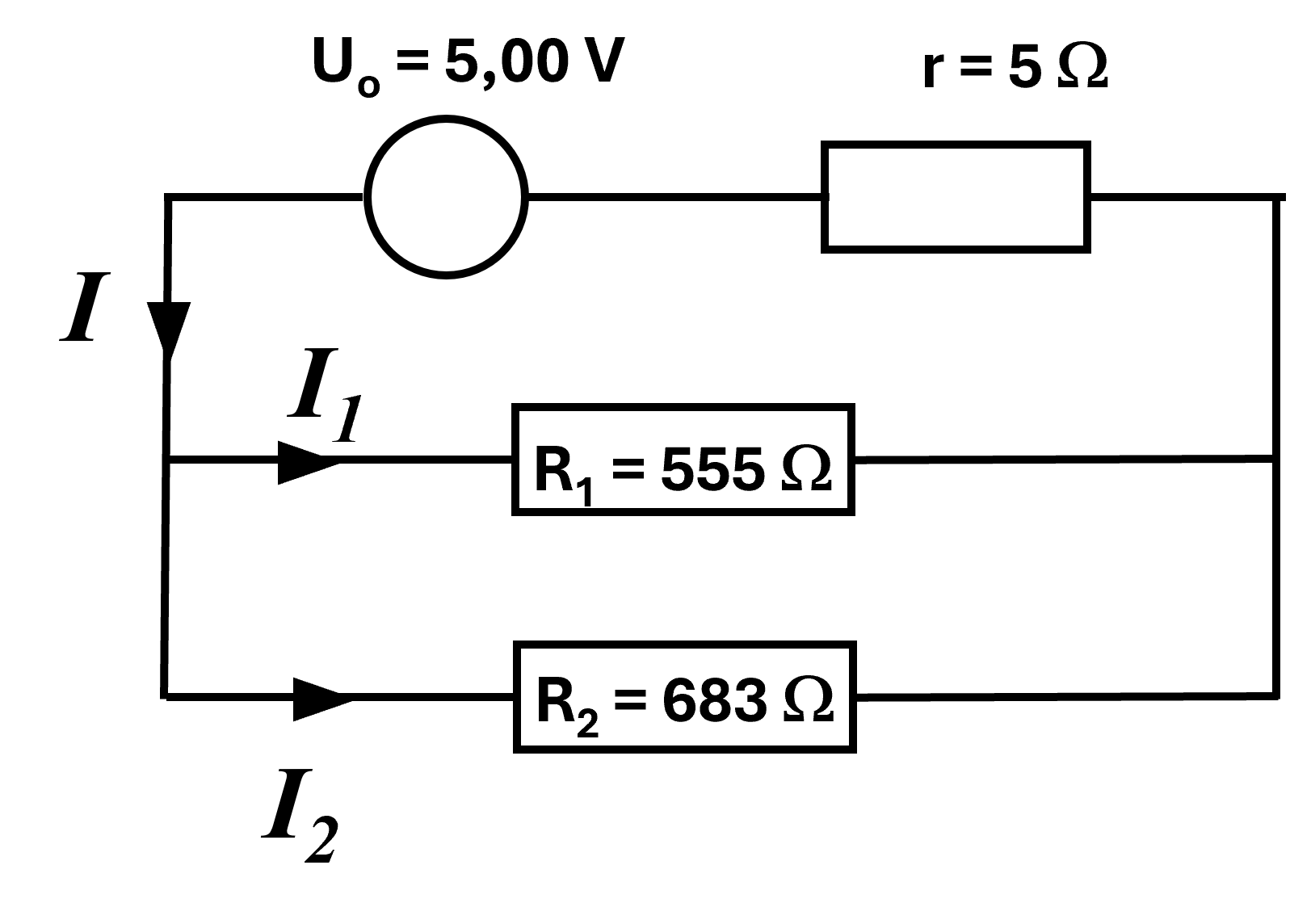
2a. Conservation de l'énergie (et donc puissance) : $U_0 \times I - r \times i^{ \ 2} \ = \ P_1 + P_2$

Soit : $r \times I^{ \ 2} - U_0 \times I \ + \ P_1 + P_2 \ = \ 0$

$\Leftrightarrow \ 5 \times I^{ \ 2} - 5,00 \times I \ + \ 79.10^{ \ -3} \ = \ 0$

La résolution de cette équation du second degré en I donne deux solutions : $I' \ = \ 16,1.10^{ \ -3} \ A \ et \ I" \ = \ 9,84.10^{ \ -1} \ A$

La valeur cherchée (inférieure à 20 mA) est donc : $I' \ = \ 16,1.10^{ \ -3} \ A$.

2b.Le rendement est : $\eta \ = \ \dfrac{P_{utile}}{P_{fournie}} \ = \ \dfrac{U_0 \times I - r \times I^{ \ 2}}{U_0 \times I}$

Soit : $\eta \ = \ \dfrac{5,00 \times 16,1.10^{ \ -3}-5 \times \left( 16,1.10^{ \ 3} \right) ^{ \ 2}}{5,00 \times 16,1.10^{ \ -3}} \ = \ 98,4 \%$

Exercice n°39 : Light emitting diode (LED).

Translation :

Le lumen (symbol : lm) est une unité de mesure de la quantité totale de lumière émise par une source. La limite théorique d'une source pour une source qui transforme l'intégralité de l'énergie électrique en énergie lumineuse, dans le spectre visible est de $683 \ lm.W^{ \ -1}$.

Une lampe fluocompacte de 25 W produit 1600 lumens.

Elle est équivalente à une lampe LED de 18 W.

1a. The theorical yield of a 25 W LED is : $\eta \ = \ \dfrac{E_u}{E_f} \ = \ \dfrac{1600}{683 \times 25} \ = \ 9,4 \%$

1b. The theorical yield of a 218 W LED is : $\eta \ = \ \dfrac{E_u}{E_f} \ = \ \dfrac{1600}{683 \times 18} \ = \ 13 \%$

2. The electrical energy electrical converted is : $E \ = \ \dfrac{25 \times 96,3}{18} \ = \ 130 \ MJ$

Exercice n°41 : Charge et décharge d'un accumulateur.

1a. $E \ = \ P \times \Delta \ t \ = \ U \times I \ \Delta \ t \ = \ U \times I^{ \ 2} \times \Delta \ t$

1b. $E \ = \ 3,20 \times \left (75,0.10^{ \ -3} \right)^{ \ 2} \times 8,00 \times 3600 \ = \ 518 \ J$

2. La puissance utile est : $E_u \ = \ 2590 - 518 \ = \ 2072 \ J$

Le rendement correspondant est $\eta \ = \ \dfrac{E_u}{E_f} \ = \ \dfrac{2072}{2590} \ = \ 80 \ \%$

3. La charge électrique accumulée a pour valeur : $Q\ = \ I \times \ \Delta \ t \ = \ 75,0.10^{ \ -3} \times 8,00 \times 3600 \ = \ 2160 \ C$

4a. L'énargie récupérée est : $E_f \ = \ \eta \times E_u \ = \ 0,80 \times 2072 \ = \ 1,66.10^{ \ 3} \ J$